蓝桥杯刷题总结---第二周

一.1441: 蓝桥杯2013年第四届真题-幸运数

幸运数是波兰数学家乌拉姆命名的。它采用与生成素数类似的“筛法”生成。 
首先从1开始写出自然数1,2,3,4,5,6,....
1  就是第一个幸运数。
我们从2这个数开始。把所有序号能被2整除的项删除，变为：
1  _  3  _  5  _  7  _  9  ....
把它们缩紧，重新记序，为：
1  3  5  7  9  ....  。这时，3为第2个幸运数，然后把所有能被3整除的序号位置的数删去。注意，是序号位置，不是那个数本身能否被3整除!!  删除的应该是5，11,  17,  ...
此时7为第3个幸运数，然后再删去序号位置能被7整除的(19,39,...)
最后剩下的序列类似：
1,  3,  7,  9,  13,  15,  21,  25,  31,  33,  37,  43,  49,  51,  63,  67,  69,  73,  75,  79,  ...

思路:

m,n为所求的区间,一开始初始化数组的时候可以直接构建一个奇数的数组,因为2不符合之后的规律

之后循环删除数组中的元素,注意顺序遍历上的时候会因为删除数组导致数组溢出,所以我们逆序删除数组

m,n=map(eval,input().split())
num=[2*i+1 for i in range(0,(n+1)//2)]#构建去除偶数的列表
i=1
while im and i

二. 1443: 蓝桥杯历届试题-数字游戏

栋栋正在和同学们玩一个数字游戏。
游戏的规则是这样的：栋栋和同学们一共n个人围坐在一圈。栋栋首先说出数字1。接下来，坐在栋栋左手边的同学要说下一个数字2。再下面的一个同学要从上一个同学说的数字往下数两个数说出来，也就是说4。下一个同学要往下数三个数，说7。依次类推。
为了使数字不至于太大，栋栋和同学们约定，当在心中数到  k-1  时，下一个数字从0开始数。例如，当k=13时，栋栋和同学们报出的前几个数依次为：
1,  2,  4,  7,  11,  3,  9,  3,  11,  7。
游戏进行了一会儿，栋栋想知道，到目前为止，他所有说出的数字的总和是多少。
 

n,k,T=map(eval,input().split())
sum_n=n*T
ans=0
j=1
for i in range(T):
    ans+=j
    j=(j+n*(1+i*n+i*n+n)//2)%k
print(ans)

三.1446: 蓝桥杯2013年第四届真题-核桃的数量

小张是软件项目经理，他带领3个开发组。工期紧，今天都在加班呢。为鼓舞士气，小张打算给每个组发一袋核桃（据传言能补脑）。他的要求是：
1.  各组的核桃数量必须相同
2.  各组内必须能平分核桃（当然是不能打碎的）
3.  尽量提供满足1,2条件的最小数量（节约闹革命嘛）

思路:用辗转相减的方法求出最大公因数,再利用最大公因数乘以最小公倍数为两数的乘积求出最小公倍数

a,b,c=map(eval,input().split())
def min_yin(i,j):
    if i==j:
        return i
    return min_yin(abs(i-j),min(i,j))
ab=a*b/min_yin(a,b)#求出a,b的最小公倍数
abc=ab*c/min_yin(ab,c)#求出a,b,c的最小公倍数
print(int(abc))

四.1454: 蓝桥杯历届试题-蚂蚁感冒

长100厘米的细长直杆子上有n只蚂蚁。它们的头有的朝左，有的朝右。
每只蚂蚁都只能沿着杆子向前爬，速度是1厘米/秒。
当两只蚂蚁碰面时，它们会同时掉头往相反的方向爬行。
这些蚂蚁中，有1只蚂蚁感冒了。并且在和其它蚂蚁碰面时，会把感冒传染给碰到的蚂蚁。
请你计算，当所有蚂蚁都爬离杆子时，有多少只蚂蚁患上了感冒。

思路:两只蚂蚁碰面并掉头相反的方向行进就相当于擦肩而过,所以只需要计算得与第一只蚂蚁相向而行的蚂蚁数量,如果不为0则计算出于与第二只蚂蚁相向而行的数量,其后的蚂蚁不进行运算

n=eval(input())
num=list(map(eval,input().split()))
ans=1#一开始就有一只蚂蚁
first=num[0]#保存第一只蚂蚁坐标
temp=False#假设没有第二只方向相反的蚂蚁
for i  in num:
    if i*first<0 and i+first<0:#判断是否运动方向相反并且可以相遇
        ans+=1
        temp=True
if temp:#存在与第一只蚂蚁运动方向相反的一只蚂蚁
    for i in num:
        if i*first>0 and first>i:#判断是否与第一只蚂蚁运动方向相同且在蚂蚁后面
            ans+=1
print(ans)

五. 1458: 蓝桥杯2013年第四届真题-错误票据

某涉密单位下发了某种票据，并要在年终全部收回。
每张票据有唯一的ID号。全年所有票据的ID号是连续的，但ID的开始数码是随机选定的。
因为工作人员疏忽，在录入ID号的时候发生了一处错误，造成了某个ID断号，另外一个ID重号。
你的任务是通过编程，找出断号的ID和重号的ID。
假设断号不可能发生在最大和最小号。

n=eval(input())
num=[]
for _ in range(n):
    s=list(map(eval,input().split()))
    for i in s:
        num.append(i)#将每一行的数据放到同一个列表
num.sort()
lou=-1
chong=-1
for i in range(len(num)-1):
    if num[i+1]==num[i]:#判断是否有重复的
        chong=num[i]
    elif num[i]+2==num[i+1]:#判断是否有数不存在
        lou=num[i]+1
print("{} {}".format(lou,chong))

六.1456: 蓝桥杯历届试题-连号区间数

小明这些天一直在思考这样一个奇怪而有趣的问题：
在1~N的某个全排列中有多少个连号区间呢？这里所说的连号区间的定义是：
如果区间[L,  R]  里的所有元素（即此排列的第L个到第R个元素）递增排序后能得到一个长度为R-L+1的“连续”数列，则称这个区间连号区间。
当N很小的时候，小明可以很快地算出答案，但是当N变大的时候，问题就不是那么简单了，现在小明需要你的帮助。

思路:连号区间满足的必要条件为|a[i]-a[j]|==|i-j|,之后则遍历每一个区间得出连号区间的数量

n=eval(input())
num=list(map(eval,input().split()))
ans=0
for i in range(n-1):
    fmax,fmin=num[i],num[i]
    for j in range(i+1,n):
        if num[j]>fmax:#更新最大值
            fmax=num[j]
        elif num[j]

七.1453: 蓝桥杯历届试题-翻硬币

小明正在玩一个“翻硬币”的游戏。
桌上放着排成一排的若干硬币。我们用  *  表示正面，用  o  表示反面（是小写字母，不是零）。
比如，可能情形是：**oo***oooo
如果同时翻转左边的两个硬币，则变为：oooo***oooo
现在小明的问题是：如果已知了初始状态和要达到的目标状态，每次只能同时翻转相邻的两个硬币,那么对特定的局面，最少要翻动多少次呢？
我们约定：把翻动相邻的两个硬币叫做一步操作。

思路:如果要同时改变相距为i的两枚硬币则需要反动硬币i次,所以将需要翻动的硬币序号保存到数组中,求出每两个之间的距离,得出最小的结果

n=input()
m=input()
num=[]
for i in range(len(n)):
    if n[i]!=m[i]:#寻找并记录需要被翻转的硬币
        num.append(i)
ans=0
for i in range(0,len(num)-1,2):
    ans+=num[i+1]-num[i]#计算硬币之间的间隔
print(ans)

八.1461: 蓝桥杯基础练习VIP-FJ的字符串

FJ在沙盘上写了这样一些字符串：
A1  =  “A”
A2  =  “ABA”
A3  =  “ABACABA”
A4  =  “ABACABADABACABA”
…  …
你能找出其中的规律并写所有的数列AN吗？

n=eval(input())
def gets(num):
    if num==1:
        return 'A'
    else:
        s=gets(num-1)+chr(ord('A')+num-1)+gets(num-1)#递归寻找所需字符串
        return s
print(gets(n))

九.1878: 蓝桥杯2017年第八届真题-青蛙跳杯子

X星球的流行宠物是青蛙，一般有两种颜色：白色和黑色。
X星球的居民喜欢把它们放在一排茶杯里，这样可以观察它们跳来跳去。如下图，有一排杯子，左边的一个是空着的，右边的杯子，每个里边有一只青蛙。

*WWWBBB
其中，W字母表示白色青蛙，B表示黑色青蛙，*表示空杯子。
X星的青蛙很有些癖好，它们只做3个动作之一：
1. 跳到相邻的空杯子里。
2. 隔着1只其它的青蛙（随便什么颜色）跳到空杯子里。
3. 隔着2只其它的青蛙（随便什么颜色）跳到空杯子里。
对于上图的局面，只要1步，就可跳成下图局面：
WWW*BBB
本题的任务就是已知初始局面，询问至少需要几步，才能跳成另一个目标局面。
输入为2行，2个串，表示初始局面和目标局面。
输出要求为一个整数，表示至少需要多少步的青蛙跳。

思路:利用bfs进行搜索,并且利用setdefault字典来保存已经遍历过的数组防止重复遍历(必须使用setdefault 或者defaultdict进行保存,否则会超时并且必须要转换成字符串,列表无法保存)

from collections import *
start=input()
end=input()
bfs=deque()#使用队列记录状态
index_x=start.index('*')
bfs.append([index_x,0,start,-1])#保存*号的位置,步数,现在的字符串(状态),上一个*位置
steps=[-1,-2,-3,1,2,3]
ans={}#记录经历过的状态防止重复
while len(bfs)!=0:
    x,step,now,pre=bfs.popleft()
    if now==end:#到达目的状态则退出循环
        print(step)
        break
    for i in steps:
        if x+i>=0 and x+i

十.1426: 蓝桥杯历届试题-九宫重排

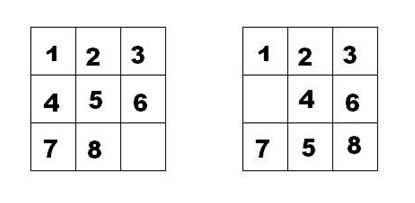
如下面第一个图的九宫格中，放着  1~8  的数字卡片，还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动，可以形成第二个图所示的局面。

我们把第一个图的局面记为：12345678.
把第二个图的局面记为：123.46758
显然是按从上到下，从左到右的顺序记录数字，空格记为句点。
本题目的任务是已知九宫的初态和终态，求最少经过多少步的移动可以到达。如果无论多少步都无法到达，则输出-1。

思路:做法同上一题,这里要注意九宫格转换成一维数组后的边界问题

from collections import *
start=input()
end=input()
bfs=deque()
index_x=start.index('.')
ans=defaultdict()
bfs.append([index_x,start,0])
while len(bfs)!=0:
    x,s,step=bfs.popleft()
    if s==end:
        print(step)
        break
    if x+3<9:#如果可以向下移动
        num=list(s)
        num[x],num[x+3]=num[x+3],num[x]
        st=''.join(num)
        if st not in ans:
            ans[st]=1
            bfs.append([x+3,st,step+1])
    if x-3>=0:#向上移动
        num=list(s)
        num[x],num[x-3]=num[x-3],num[x]
        st=''.join(num)
        if st not in ans:
            ans[st]=1
            bfs.append([x-3,st,step+1])
    if x%3!=0 :#向左移动
        num = list(s)
        num[x], num[x - 1] = num[x - 1], num[x]
        st = ''.join(num)
        if st not in ans:
            ans[st] = 1
            bfs.append([x - 1, st, step + 1])
    if (x+1)%3!=0:#向右移动
        num = list(s)
        num[x], num[x +1] = num[x+1], num[x]
        st = ''.join(num)
        if st not in ans:
            ans[st] = 1
            bfs.append([x+1, st, step + 1])

十一.1436: 蓝桥杯2014年第五届真题-地宫取宝

X  国王有一个地宫宝库。是  n  x  m  个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。
地宫的入口在左上角，出口在右下角。
小明被带到地宫的入口，国王要求他只能向右或向下行走。
走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。
当小明走到出口时，如果他手中的宝贝恰好是k件，则这些宝贝就可以送给小明。
请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这k件宝贝。

思路:采用动态规划的方法进行运算,dp[i][j][k][famx]的含义是在第i ,j个格子上当手上有k件物品时手上可以拿到价值为fmax的物品(上界)(不是当前最高的价值,是下一次所拿物品的最高价值),最后的所求结果为dp[n][m][k][12]

n,m,k=map(eval,input().split())
grid1=[list(map(eval,input().split())) for _ in range(n)]#保存最初的地图
grid=[[0 for _ in range(m+1)]]#给当前的地图最上方,最左列加上一行一列
for i in range(n):
    temp=[0]
    for j in range(m):
        temp.append(grid1[i][j])
    grid.append(temp)
dp=[[[[0 for _ in range(13)]for __ in range(k+1)]for ___ in range(m+1)] for ____ in range(n+1)]#初始化dp数组
for i in range(1,n+1):
    for j in range(1,m+1):
        for num in range(0,k+1):
            for fmax in range(13):
                if i==1 and j==1 :
                    if num==0 or(num==1 and fmax>grid[i][j]):#初始化dp数组,num==0不拿第一个 num==1拿第一个
                        dp[i][j][num][fmax]=1
                    continue
                s1=0
                if num!=0 and fmax>grid[i][j]:#如果可以拿
                    s1=dp[i-1][j][num-1][grid[i][j]]+dp[i][j-1][num-1][grid[i][j]]
                s2=dp[i-1][j][num][fmax]+dp[i][j-1][num][fmax]#如果不拿
                dp[i][j][num][fmax]=(s1+s2)%1000000007
print(dp[n][m][k][12])

十二.1439: 蓝桥杯历届试题-小朋友排队

n  个小朋友站成一排。现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。开始的时候，所有小朋友的不高兴程度都是0。
如果某个小朋友第一次被要求交换，则他的不高兴程度增加1，如果第二次要求他交换，则他的不高兴程度增加2（即不高兴程度为3），依次类推。当要求某个小朋友第k次交换时，他的不高兴程度增加k。
请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。
样例说明
首先交换身高为3和2的小朋友，再交换身高为3和1的小朋友，再交换身高为2和1的小朋友，每个小朋友的不高兴程度都是3，总和为9。
思路:每个小朋友需要交换的次数为在小朋友前面并且比小朋友高的数量加上在小朋友后面并且比小朋友低的数量,即逆序对的数量,所以构造树状数组以复杂度为O(nlogn)来设计算法,这里需要注意应该在小朋友身高加一避免小朋友身高出现0的情况,因为minbit(0)==0 会使程序进入死循环

 

n=eval(input())
nums=list(map(eval,input().split()))#保存初始身高
for i in range(len(nums)):#初始身高加一
    nums[i]+=1
m=max(nums)#求出身高最大值,按照身高构造树状数组
c=[0 for _ in range(m+5)]
def minbit(x):#求出下一层的间隔
    return x&(-x)
def addx(x,fmax):#插入一个数
    i=x
    global c
    while i<=fmax+1:#对所被包含的每一层进行更新
        c[i]+=1
        i+=minbit(i)#求出下一层的坐标
def sumx(x):
    global c
    i=x
    ans=0
    while i>0:#倒序求出前缀和
        ans+=c[i]
        i-=minbit(i)
    return ans
numl=[0 for _ in range(n)]#构建逆序对的数组
for i in range(n):
    addx(nums[i],m)#将这个身高放入树状数组
    numl[i]=i+1-sumx(nums[i])#求出在这个人之前比他高的人
for i in range(m+5):
    c[i]=0#清空数组
for i in range(n-1,-1,-1):#倒序求出在这个人之后比他矮的人数
    addx(nums[i],m)
    numl[i]+=sumx(nums[i]-1)
ans=0
for i in range(n):
    ans+=(1+numl[i])*numl[i]//2#利用高斯求和
print(ans)