最小二乘曲线拟合原理,平面曲线与空间曲线,并附python实现demo
1.最小二乘思想
1.1 基本描述
最小二乘法是一种在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域得到广泛应用的数学工具。
1.2 定义
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
1.3 应用范围
最小二乘法可用于曲线拟合,其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
以上引用于 <<百度百科>>词条:最小二乘
1.4 个人理解
所谓最小二乘的算法,主要思想就是“所有的值”的平方加起来取最小的值,从而求得最小值的时候带求未知数此时的值。而核心就是如何求得平方和最小哪个位置的点:通常方法为求偏导数,使其等于0那一点。
2.最小二乘拟合曲线
2.1 拟合基本思想
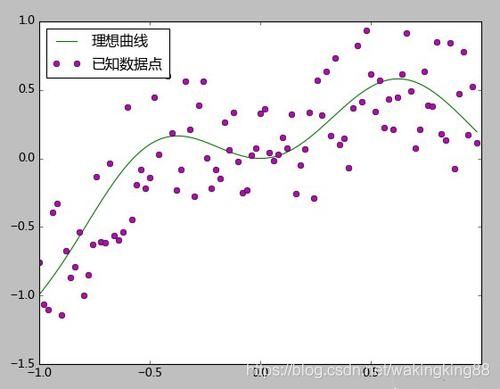
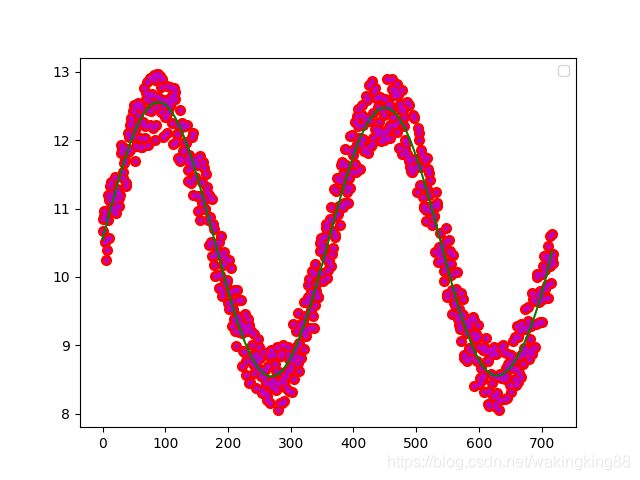
拟合的概念描述: 多个散点拟合成曲线,但前提要指定是多少次幂的曲线,通常为一元多次曲线方程。效果图入下所示:
已知: 散点数据,共有n个点.
[ ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) . . . . ( x n , y n ) ] [(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})....(x_{n},y_{n})] [(x1,y1),(x2,y2),(x3,y3)....(xn,yn)]
待求: 一元多次曲线公式,假设最高阶为k.
y = a 0 + a 1 x + a 2 x 2 + . . . + a n x k = F ( x ) (1) y=a_{0}+a_{1}x+a_{2}x^2+...+a_{n}x^k=F(x) \tag{1} y=a0+a1x+a2x2+...+anxk=F(x)(1)
2.2.1目标函数
描述: 多点拟合成曲线,若选择出最优曲线,原则为(也是这类最小二乘的核心思想):散点到曲线距离的和的绝对值最小。BUT!but! But! 点到直线的距离并不是像点到直线的距离公式那么求的,如果那样求的话,点到曲线的距离公式要相当的麻烦。 故,这里为了简化计算又不影响整体思想,采用x值和y值的差值的绝对值来进行衡量。即 ∣ x i − x ∣ 和 ∣ y i − y ∣ |x_{i}-x|和|y_{i}-y| ∣xi−x∣和∣yi−y∣的值取相对最小值,为了计算再简化,取未知点 ( x , y ) (x,y) (x,y)为 ( x i , F ( x i ) ) (x_{i},F(x_{i})) (xi,F(xi)),这样 X X X方向的差值就为0,所以只用关心 Y Y Y 方向的差值 ∣ y i − F ( x i ) ∣ |y_{i}-F(x_{i})| ∣yi−F(xi)∣即可.最终的目标是所有点的Y方向的差值的平方和最小.
最终的目标函数为:
m i n ∑ i = 1 n ( y i − F ( x i ) ) 2 (2) min\sum_{i=1}^n(y_{i}-F(x_{i}))^2 \tag{2} mini=1∑n(yi−F(xi))2(2)
2.3 公式推导
- 设各个点的偏差和为R,n为散点个数,k为多项式的最高阶数.由公式2目标函数得:
R 2 = ∑ i = 1 n [ y i − ( a 0 + a 1 x i + a 2 x i 2 + . . . + a n x i k ) ] 2 (3) R^2=\sum_{i=1}^n[y_{i}-(a_{0}+a_{1}x_{i}+a_{2}x_{i}^2+...+a_{n}x_{i}^k)]^2 \tag{3} R2=i=1∑n[yi−(a0+a1xi+a2xi2+...+anxik)]2(3) - 为了求得符合条件的 a i a_{i} ai值,对等式右边求 a i a_{i} ai偏导数,正常情况下导数为零点即为极值点,而依据所求得的一元多次方程的特性与实际曲线的存在情况,应该只有一个极小值符合情况.进一步推论得到每一个 a i a_i ai的偏导数都应该为0,最终联合解算的 a i a_i ai值才为最终多项式的系数.过程为如下::
∂ R ∂ a 0 = − 2 ∑ i = 1 n [ y i − ( a 0 + a 1 x i + a 2 x i 2 + . . . + a k x i k ) ] ∗ ∂ a 0 ∂ a 0 = 0 \frac{\partial R}{\partial a_{0}} =-2\sum_{i=1}^n[y_{i}-(a_{0}+a_{1}x_{i}+a_{2}x_{i}^2+...+a_{k}x_{i}^k)]*\frac{\partial a_{0}}{\partial a_{0}}=0 ∂a0∂R=−2i=1∑n[yi−(a0+a1xi+a2xi2+...+akxik)]∗∂a0∂a0=0
∂ R ∂ a 1 = − 2 ∑ i = 1 n [ y i − ( a 0 + a 1 x i + a 2 x i 2 + . . . + a k x i k ) ] ∗ ∂ a 1 ∂ a 1 ∗ x i 1 = 0 \frac{\partial R}{\partial a_{1}} =-2\sum_{i=1}^n[y_{i}-(a_{0}+a_{1}x_{i}+a_{2}x_{i}^2+...+a_{k}x_{i}^k)]*\frac{\partial a_{1}}{\partial a_{1}}*x_{i}^1=0 ∂a1∂R=−2i=1∑n[yi−(a0+a1xi+a2xi2+...+akxik)]∗∂a1∂a1∗xi1=0
∂ R ∂ a 2 = − 2 ∑ i = 1 n [ y i − ( a 0 + a 1 x i + a 2 x i 2 + . . . + a k x i k ) ] ∗ ∂ a 2 ∂ a 2 ∗ x i 2 = 0 \frac{\partial R}{\partial a_{2}} =-2\sum_{i=1}^n[y_{i}-(a_{0}+a_{1}x_{i}+a_{2}x_{i}^2+...+a_{k}x_{i}^k)]*\frac{\partial a_{2}}{\partial a_{2}}*x_{i}^2=0 ∂a2∂R=−2i=1∑n[yi−(a0+a1xi+a2xi2+...+akxik)]∗∂a2∂a2∗xi2=0
. . . ... ...
. . . ... ...
. . . ... ...
∂ R ∂ a n = − 2 ∑ i = 1 n [ y i − ( a 0 + a 1 x i + a 2 x i 2 + . . . + a k x i k ) ] ∗ ∂ a k ∂ a k ∗ x i k = 0 \frac{\partial R}{\partial a_{n}} =-2\sum_{i=1}^n[y_{i}-(a_{0}+a_{1}x_{i}+a_{2}x_{i}^2+...+a_{k}x_{i}^k)]*\frac{\partial a_{k}}{\partial a_{k}}*x_{i}^k=0 ∂an∂R=−2i=1∑n[yi−(a0+a1xi+a2xi2+...+akxik)]∗∂ak∂ak∗xik=0
. . . . . . (4) ......\tag{4} ......(4)
- 将等式整理下,然后应该可以得到下面的等式:
∑ i = 1 n [ ( a 0 + a 1 x i + a 2 x i 2 + . . . + a k x i k ) ] ∗ ∂ a 0 ∂ a 0 ∗ x i 0 = ∑ i = 1 n y i ∗ x i 0 \sum_{i=1}^n[(a_{0}+a_{1}x_{i}+a_{2}x_{i}^2+...+a_{k}x_{i}^k)]*\frac{\partial a_{0}}{\partial a_{0}}*x_{i}^0=\sum_{i=1}^ny_{i}*x_{i}^0 i=1∑n[(a0+a1xi+a2xi2+...+akxik)]∗∂a0∂a0∗xi0=i=1∑nyi∗xi0
∑ i = 1 n [ ( a 0 + a 1 x i + a 2 x i 2 + . . . + a k x i k ) ] ∗ ∂ a 1 ∂ a 1 ∗ x i 1 = ∑ i = 1 n y i ∗ x i 1 \sum_{i=1}^n[(a_{0}+a_{1}x_{i}+a_{2}x_{i}^2+...+a_{k}x_{i}^k)]*\frac{\partial a_{1}}{\partial a_{1}}*x_{i}^1=\sum_{i=1}^ny_{i}*x_{i}^1 i=1∑n[(a0+a1xi+a2xi2+...+akxik)]∗∂a1∂a1∗xi1=i=1∑nyi∗xi1
∑ i = 1 n [ ( a 0 + a 1 x i + a 2 x i 2 + . . . + a k x i k ) ] ∗ ∂ a 2 ∂ a 2 ∗ x i 2 = ∑ i = 1 n y i ∗ x i 2 \sum_{i=1}^n[(a_{0}+a_{1}x_{i}+a_{2}x_{i}^2+...+a_{k}x_{i}^k)]*\frac{\partial a_{2}}{\partial a_{2}}*x_{i}^2=\sum_{i=1}^ny_{i}*x_{i}^2 i=1∑n[(a0+a1xi+a2xi2+...+akxik)]∗∂a2∂a2∗xi2=i=1∑nyi∗xi2
. . . ... ...
. . . ... ...
. . . ... ...
∑ i = 1 n [ ( a 0 + a 1 x i + a 2 x i 2 + . . . + a k x i k ) ] ∗ ∂ a k ∂ a k ∗ x i k = ∑ i = 1 n y i ∗ x i k \sum_{i=1}^n[(a_{0}+a_{1}x_{i}+a_{2}x_{i}^2+...+a_{k}x_{i}^k)]*\frac{\partial a_{k}}{\partial a_{k}}*x_{i}^k=\sum_{i=1}^ny_{i}*x_{i}^k i=1∑n[(a0+a1xi+a2xi2+...+akxik)]∗∂ak∂ak∗xik=i=1∑nyi∗xik
. . . . . . (5) ......\tag{5} ......(5)
-
将等式左边进行一下化简,然后应该可以得到下面的等式:
n ∗ a 0 + a 1 ∑ i = 1 n x i + . . . + a k ∑ i = 1 n x i k = ∑ i = 1 n y i ∗ x i 0 n*a_0+a_{1}\sum_{i=1}^nx_{i}+...+a_{k}\sum_{i=1}^nx_{i}^k=\sum_{i=1}^ny_{i}*x_{i}^0 n∗a0+a1i=1∑nxi+...+aki=1∑nxik=i=1∑nyi∗xi0
a 0 ∑ i = 1 n x i + a 1 ∑ i = 1 n x i 2 + . . . + a k ∑ i = 1 n x i k + 1 = ∑ i = 1 n y i ∗ x 1 a_0\sum_{i=1}^nx_{i}+a_{1}\sum_{i=1}^nx_{i}^2+...+a_{k}\sum_{i=1}^nx_{i}^{k+1}=\sum_{i=1}^ny_{i}*x^1 a0i=1∑nxi+a1i=1∑nxi2+...+aki=1∑nxik+1=i=1∑nyi∗x1
a 0 ∑ i = 1 n x i 2 + a 1 ∑ i = 1 n x i 3 + . . . + a k ∑ i = 1 n x i k + 2 = ∑ i = 1 n y i ∗ x i 2 a_0\sum_{i=1}^nx_{i}^2+a_{1}\sum_{i=1}^nx_{i}^3+...+a_{k}\sum_{i=1}^nx_{i}^{k+2}=\sum_{i=1}^ny_{i}*x_{i}^2 a0i=1∑nxi2+a1i=1∑nxi3+...+aki=1∑nxik+2=i=1∑nyi∗xi2
. . . ... ...
. . . ... ...
. . . ... ...
a 0 ∑ i = 1 n x i k + a 1 ∑ i = 1 n x i k + 1 + . . . + a k ∑ i = 1 n x i 2 k = ∑ i = 1 n y i ∗ x i k a_0\sum_{i=1}^nx_{i}^k+a_{1}\sum_{i=1}^nx_{i}^{k+1}+...+a_{k}\sum_{i=1}^nx_{i}^{2k}=\sum_{i=1}^ny_{i}*x_{i}^k a0i=1∑nxik+a1i=1∑nxik+1+...+aki=1∑nxi2k=i=1∑nyi∗xik
. . . . . . (6) ......\tag{6} ......(6) -
把这些等式表示成矩阵的形式,就可以得到下面的矩阵:
[ n ∑ i = 1 n x i ⋯ ∑ i = 1 n x i k ∑ i = 1 n x i ∑ i = 1 n x i 2 ⋯ ∑ i = 1 n x i k + 1 ⋮ ⋱ ⋮ ⋯ ∑ i = 1 n x i k ∑ i = 1 n x i k + 1 ⋯ ∑ i = 1 n x i 2 k ] [ a 0 a 1 ⋯ a k ] = [ ∑ i = 1 n y i ∗ x i 0 ∑ i = 1 n y i ∗ x i 1 ⋯ ∑ i = 1 n y i ∗ x i k ] = [ ∑ i = 1 n y i ∑ i = 1 n y i ∗ x i 1 ⋯ ∑ i = 1 n y i ∗ x i k ] \begin{bmatrix} n & \sum_{i=1}^nx_{i}&\cdots & \sum_{i=1}^nx_{i}^k \\ \sum_{i=1}^nx_{i}&\sum_{i=1}^nx_{i}^2& \cdots&\sum_{i=1}^nx_{i}^{k+1} \\ \vdots & \ddots & \vdots&\cdots \\ \sum_{i=1}^nx_{i}^k &\sum_{i=1}^nx_{i}^{k+1}& \cdots & \sum_{i=1}^nx_{i}^{2k} \end{bmatrix} \left[ \begin{matrix} \ a_0\\ \ a_1\\ \ \cdots\\ \ a_k\\ \end{matrix} \right]= \left[ \begin{matrix} \ \sum_{i=1}^ny_{i}*x_{i}^0\\ \ \sum_{i=1}^ny_{i}*x_{i}^1\\ \ \cdots\\ \ \sum_{i=1}^ny_{i}*x_{i}^k\\ \end{matrix} \right]= \left[ \begin{matrix} \ \sum_{i=1}^ny_{i}\\ \ \sum_{i=1}^ny_{i}*x_{i}^1\\ \ \cdots\\ \ \sum_{i=1}^ny_{i}*x_{i}^k\\ \end{matrix} \right] ⎣⎢⎢⎢⎡n∑i=1nxi⋮∑i=1nxik∑i=1nxi∑i=1nxi2⋱∑i=1nxik+1⋯⋯⋮⋯∑i=1nxik∑i=1nxik+1⋯∑i=1nxi2k⎦⎥⎥⎥⎤⎣⎢⎢⎡ a0 a1 ⋯ ak⎦⎥⎥⎤=⎣⎢⎢⎡ ∑i=1nyi∗xi0 ∑i=1nyi∗xi1 ⋯ ∑i=1nyi∗xik⎦⎥⎥⎤=⎣⎢⎢⎡ ∑i=1nyi ∑i=1nyi∗xi1 ⋯ ∑i=1nyi∗xik⎦⎥⎥⎤
. . . . . . (7) ......\tag{7} ......(7)
-
将这个范德蒙得矩阵化简后(此公式为一种理想模式,符号跟之前的没有关系,只是说明可以化简到下面这样的模式,方便讲解运算)可得到:
J F = [ 1 x 1 ⋯ x 1 k 1 x 2 ⋯ x 2 k ⋮ ⋱ ⋮ ⋯ 1 x n ⋯ x n k ] [ a 0 a 1 ⋯ a k ] = [ y 1 y 2 ⋯ y n ] {{\mathbf{J}}_{F}}=\begin{bmatrix} 1 & x_1&\cdots & x_{1}^k \\ 1&x_2& \cdots&x_2^{k} \\ \vdots & \ddots & \vdots&\cdots \\ 1&x_n& \cdots & x_n^{k} \end{bmatrix} \left[ \begin{matrix} \ a_0\\ \ a_1\\ \ \cdots\\ \ a_k\\ \end{matrix} \right]= \left[ \begin{matrix} \ y_{1}\\ \ y_{2}\\ \ \cdots\\ \ y_{n}\\ \end{matrix} \right] JF=⎣⎢⎢⎢⎡11⋮1x1x2⋱xn⋯⋯⋮⋯x1kx2k⋯xnk⎦⎥⎥⎥⎤⎣⎢⎢⎡ a0 a1 ⋯ ak⎦⎥⎥⎤=⎣⎢⎢⎡ y1 y2 ⋯ yn⎦⎥⎥⎤
. . . . . . (8) ......\tag{8} ......(8) -
也就是说最终简化为矩阵运算 X ∗ A = Y X*A=Y X∗A=Y求 A A A的问题,那么 A = Y ∗ X − 1 A =Y*X^{-1} A=Y∗X−1,便得到了系数矩阵 A A A,同时,我们也就得到了拟合曲线.
注意: 这里 X X X是已知数, A A A是未知数,其中最复杂的就是求矩阵 A A A的系数 X X X的过程,一定要细心.
3.拓展
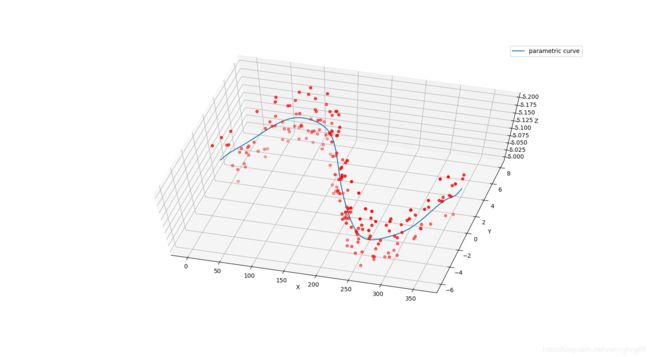
3.1 空间曲线最小二乘拟合
已知: 空间内的点 ( x 1 , y 1 , z 1 ) , ( x 2 , y 2 , z 2 ) , ( x 3 , y 3 , z 3 ) . . . ( x n , y n , z n ) (x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)...(x_n,y_n,z_n) (x1,y1,z1),(x2,y2,z2),(x3,y3,z3)...(xn,yn,zn)
所要拟合的多项式直线的最高次幂: k k k
**待求:**多项式表达式
z = a 0 + a 1 x + a 2 x 2 + . . . + a n x k + b 0 + b 1 y + b 2 y 2 + . . . + b n y k = F ( x , y ) z=a_{0}+a_{1}x+a_{2}x^2+...+a_{n}x^k+b_{0}+b_{1}y+b_{2}y^2+...+b_{n}y^k=F(x,y) z=a0+a1x+a2x2+...+anxk+b0+b1y+b2y2+...+bnyk=F(x,y)
根据经典最小二乘算法可以拓展到加权最小二乘算法等,具体应用场景可以查询相关资料.
求解思路: 投影法.也就是把三维问题化成二维问题来解决.也就是将空间曲线F(x,y,z)投影到x,y平面和y,z平面即可.只用投影到两个平面即可.因为投影后空间曲线就变成空间曲面了,而两次投影生成两个曲面,而两个曲面就可以确定一个,且唯一一个空间曲线.故连个空间曲面的方程联立后就是所求的空间曲线.
**公式推导部分:**基本同上二维部分.
假设在x,y平面和y,z平面求空间曲面
注意空间点 p ( x n , y n , z n ) p(x_n,y_n,z_n) p(xn,yn,zn)在使用时,要每次带入对应的投影面的值,比如在xy平面,已知值为 p x y ( x n , y n ) p_{xy}(x_n,y_n) pxy(xn,yn),在yz平面时,已知点值为 p y z ( y n , z n ) p_{yz}(y_n,z_n) pyz(yn,zn).
然后根据上面平面最小二乘拟合公式分别在每个投影面求得平面方程为:
y = a 0 + a 1 x + a 2 x 2 + . . . + a n x k (9) y=a_{0}+a_{1}x+a_{2}x^2+...+a_{n}x^k \tag{9} y=a0+a1x+a2x2+...+anxk(9)
z = b 0 + b 1 y + b 2 y 2 + . . . + b n y k (10) z=b_{0}+b_{1}y+b_{2}y^2+...+b_{n}y^k \tag{10} z=b0+b1y+b2y2+...+bnyk(10)
最后公式9与公式10联立,既可以求得看见曲线方程,形式大致为:
z = a 0 ′ + a 1 ′ x + a 2 ′ x 2 + . . . + a n ′ x k + b 0 ′ + b 1 ′ y + b 2 ′ y 2 + . . . + b n ′ y k (11) z=a_{0}'+a_{1}'x+a_{2}'x^2+...+a_{n}'x^k+b_{0}'+b_{1}'y+b_{2}'y^2+...+b_{n}'y^k\tag{11} z=a0′+a1′x+a2′x2+...+an′xk+b0′+b1′y+b2′y2+...+bn′yk(11)
4.参考文献
https://blog.csdn.net/neuldp/article/details/52049367
https://www.cnblogs.com/paiandlu/p/7843236.html
https://www.datalearner.com/blog/1051539222770649
5.示例代码
点击跳转下载链接
demo里含平面曲线(2D)和空间曲线(3D)的实现源码,并通过画图软件实时的二维或者三维展示