八大排序算法详解（通俗易懂）

---

前言

所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法在很多领域得到相当地重视，尤其是在大量数据的处理方面，一个优秀的算法可以节省大量的资源。

---

一、八大排序算法：

1.直接插入排序：

直接插入排序就是把待排序的元素逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。

实际中我们玩扑克牌时，就用了插入排序的思想

动图演示：

那比如给我们一段序列，代码如何实现呢？
我们可以把第一个元素看成有序序列（一个元素序列必然有序）进行多次单趟插排

void InsertSort(int* arr, int size)//直接插入排序
{
	for (int i = 0; i < size - 1; i++)
	{
		//单趟插入排序
		//基本思想：[0,end]区间值为有序
		int end = i;
		int tmp = arr[end + 1];
		while (end >= 0)
		{
			if (tmp < arr[end])
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else
			{
				break;//在这里break出去再去赋值tmp是为了防止最后一次end = -1进不来赋值
			}
		}
		arr[end + 1] = tmp;
	}
}

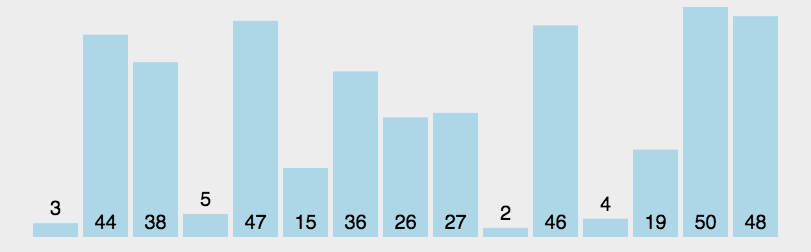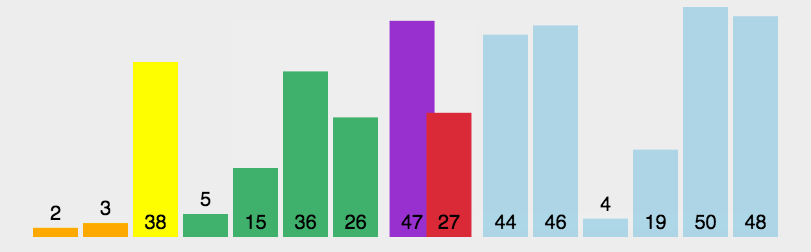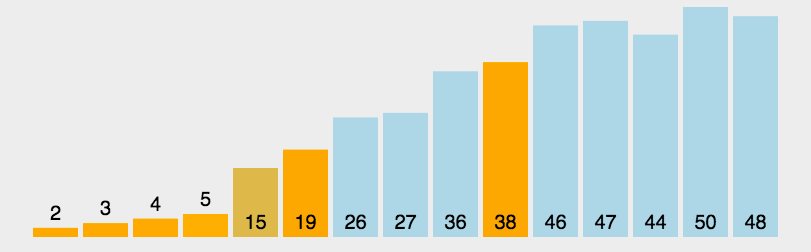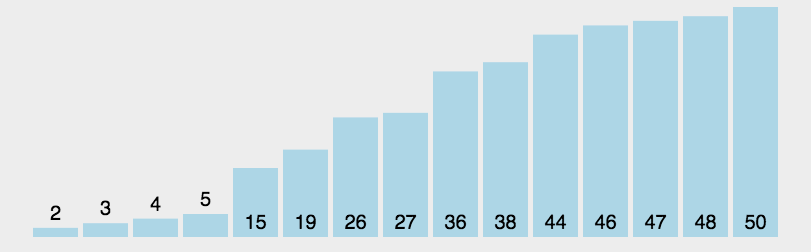
2.希尔排序：

希尔排序是对直接插入排序的优化，它对序列先进行多次预排序使之接近有序，因为最后接近有序使用直接插入排序非常快。

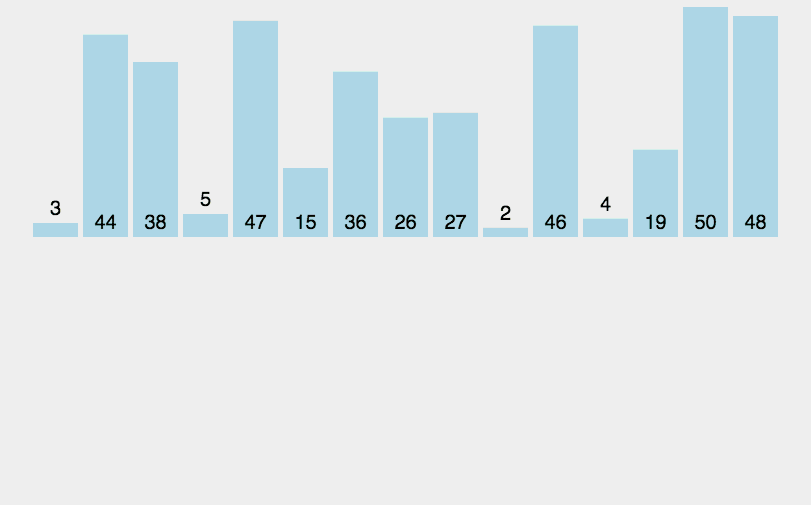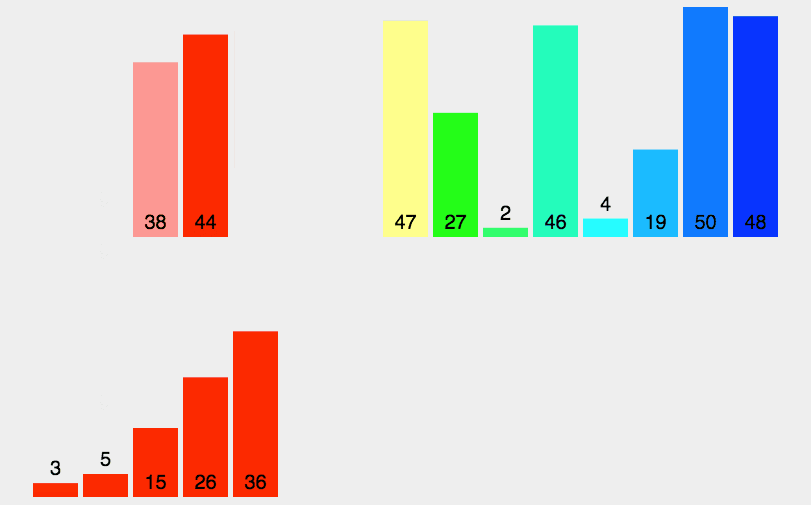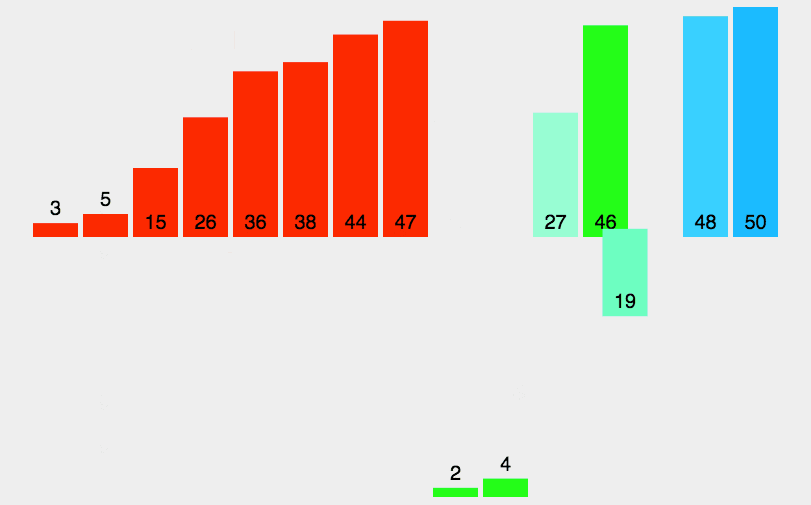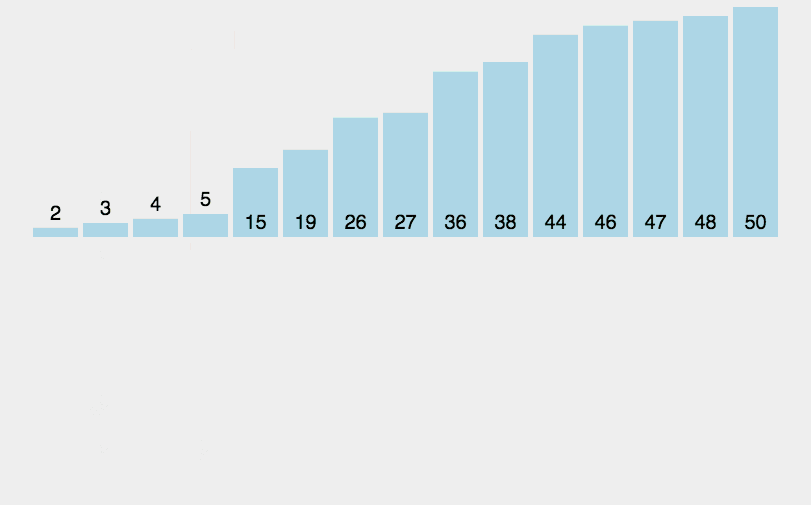
如图所示：

• 当gap越大，预排序越快，但是越不接近有序
• 当gap越小，数据处理越慢，越接近有序
• 当gap为1即直接插入排序

如下代码所示：所以我们可以对gap进行动态改变

void ShellSort(int* arr, int size)//希尔排序
{
	int gap = size;
	//多次预排+最后一次直接插入排序
	while (gap > 1)
	{
		gap = gap / 3 + 1;//控制最后一次进来gap为1进行直接插入排序
		for (int i = 0; i < size - gap; i++)
		{
			int end = i;
			int tmp = arr[end + gap];
			while (end >= 0)
			{
				if (tmp < arr[end])
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			arr[end + gap] = tmp;
		}
	}
}

3.选择排序:

选择排序在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后以此类推，直到所有元素均排序完毕。

动图演示:
我们实际可以在一次遍历中同时找到最小和最大的值：

void SelectSort(int* arr, int size)//优化选择排序
{
	int begin = 0;
	int end = size - 1;
	while (begin < end)
	{
		int mini = begin, maxi = begin;
		for (int i = begin + 1; i <= end; i++)
		{
			if (arr[i] < arr[mini])
			{
				mini = i;
			}
			if (arr[i] > arr[maxi])
			{
				maxi = i;
			}
		}
		Swap(&arr[mini], &arr[begin]);
		//如果maxi = begin，上一步交换了begin和mini的值，会影响maxi指向的值
		if (maxi == begin)
		{
			maxi = mini;
		}
		Swap(&arr[maxi], &arr[end]);
		begin++;
		end--;
	}
}

4.堆排序:

堆排序可以看之前这篇：二叉树和堆详解（通俗易懂）

5.冒泡排序:

冒泡排序也是通过遍历比较左右值得大小，例如排升序即左值大于右值交换，最后最大值即排到最右边。

动图演示：

void BubbleSort(int* arr, int size)//冒泡排序
{
	for (int i = 1; i < size; i++)
	{
		int flag = 0;
		for (int j = 0; j < size - i; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				Swap(&arr[j], &arr[j + 1]);
				flag++;
			}
		}
		if (flag == 0)
		{
			break;
		}
	}
}

6.快速排序:

这边讲解的是快速排序的前后指针法：

1. 首先选择一个keyi位置，一般为序列首。
2. 创建两个指针，prev指向keyi，cur指向prev+1
3. cur往右找小于keyi位置的值，如果找到了prev往前找大于keyi位置的值，然后交换cur和prev位置的值（注意，这里既然cur找到arr[cur]>arr[keyi],那么cur和prev之间的值必然都会大于arr[keyi]）
4. 最后cur走完序列，再把keyi和prev位置值交换，这样keyi左边都会比他小，右边都会比他大
5. 再将区间分为[begin,keyi-1],[keyi+1,end]继续递归直至有序

动图演示：

7.归并排序:

归并排序将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

动图演示：

void _MergeSort(int* arr, int begin, int end, int* tmp)
{
	if (begin >= end)
	{
		return;
	}

	//递归找有序区间
	int mid = (end + begin) / 2;
	//[begin, mid][mid+1,end]
	_MergeSort(arr, begin, mid, tmp);
	_MergeSort(arr,mid + 1, end, tmp);

	//左右区间归并有序
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin1;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] <= arr[begin2])
		{
			tmp[i++] = arr[begin1++];
		}
		else
		{
			tmp[i++] = arr[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[i++] = arr[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = arr[begin2++];
	}

	//辅助数组tmp中数据返回拷贝到原数组
	memcpy(arr + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}

void MergeSort(int* arr, int size)//归并排序
{
	int* tmp = (int*)malloc(sizeof(int) * size);
	if (tmp == NULL)
	{
		perror("malloc:fail");
		exit(-1);
	}

	int begin = 0;
	int end = size - 1;

	_MergeSort(arr, begin, end, tmp);
}

8.计数排序:

1. 统计相同元素出现次数根据
2. 统计的结果将序列回收到原来的序列中
3. 计数排序只适用于范围集中且重复数据较高的数据

动图演示：

//计数排序只适用于范围集中且重复数据较高的数据
void CountSort(int* arr, int size)//计数排序
{
	int min = arr[0];
	int max = arr[0];
	for (int i = 1; i < size; i++)
	{
		if (arr[i] < min)
		{
			min = arr[i];
		}
		if (arr[i] > max)
		{
			max = arr[i];
		}
	}
	
	//计数数组count
	int range = max - min + 1;
	int* count = (int*)malloc(sizeof(int) * range);
	if (count == NULL)
	{
		perror("malloc:fail");
		exit(-1);
	}
	memset(count, 0, sizeof(int) * range);

	//开始计数
	for (int i = 0; i < size; i++)
	{
		count[arr[i] - min]++;
	}
	
	//回写排序
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			arr[j++] = i + min;
		}
	}
}

二、八大排序算法总结：

排序算法	时间复杂度（平均）	时间复杂度（最坏）	时间复杂度（最好）	空间复杂度	稳定性
插入排序	O(N^2)	O(N^2)	O(N)	O(1)	稳定
希尔排序	O(N^1.3)	O(N^2)	O(N)	O(1)	不稳定
选择排序	O(N^2)	O(N^2)	O(N^2)	O(1)	不稳定
堆排序	O(N*log2(N))	O(N*log2(N))	O(N*log2(N))	O(1)	不稳定
冒泡排序	O(N^2)	O(N^2)	O(N)	O(1)	稳定
快速排序	O(N*log2(N))	O(N^2)	O(N*log2(N))	O(N*log2(N))	不稳定
归并排序	O(N*log2(N))	O(N*log2(N))	O(N*log2(N))	O(N)	稳定
计数排序	O(N+K)	O(N+K)	O(N+K)	O(N+K)	稳定

---

总结

以上就是今天要讲八大排序算法的内容，如果对刚刚阅读本篇博客的你有所帮助，请给博主一个三连哦！