【温故而知新】计算机408之数据结构速记

知识学了又忘，知识忘了又学，所以我做了速记版本，用自己的理解记录各学科我认为比较重要的知识点，方便复习记忆。

时间复杂度？

答：一个语句的频度是指该语句在算法中被重复执行的次数。时间复杂度是算法中所有语句的频度之和的数量级。算法的时间复杂度不仅依赖于问题的规模n, 也取决于待输入数据的性质（如输入数据元素的初始状态）。

空间复杂度？

答：算法的空间复杂度S(n)定义为该算法所耗费的存储空间。算法原地工作是指算法所需的辅助空间为常量。

排序算法？

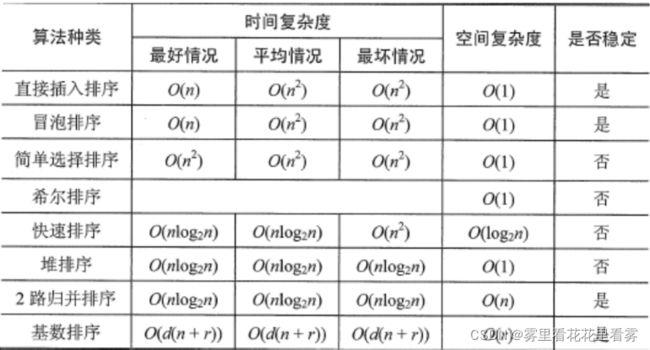
答：插入排序（直接插入排序、折半插入排序、希尔排序）、交换排序（冒泡排序、快速排序）、选择排序（简单选择排序、堆排序）、归并排序、基数排序。

直接插入排序（稳定）：基本思想为：将序列分为有序部分和无序部分，从无序部分依次选择元素与有序部分比较找到合适的位置，将原来的元素往后移，将元素插入到相应位置上。

折半插入排序（稳定）：基本思想为：对序列中的每个元素做以上处理，找到合适位置将其他元素后移进行插入。优点是：比较次数大大减少。

希尔排序（不稳定）：基本思想为：先将序列分为若干个子序列，对各子序列进行直接插入排序，等到序列基本有序时再对整个序列进行一次直接插入排序。

简单选择排序（不稳定）：基本思想为：将序列分为2部分，每经过一趟就在无序部分找到一个最小值然后与无序部分的第一个元素交换位置。

堆排序（不稳定）：基本思想为：让此序列排列成完全二叉树，该树具有以下特点，该树中任意节点均大于或小于其左右孩子，此树的根节点为最大值或者最小值。

冒泡排序（稳定）：基本思路为：每一趟都将元素进行两两比较，并且按照“前小后大”的规则进行交换。

快速排序（不稳定）：基本思路为：在序列中任意选择一个元素作为中心，比它大的元素一律向后移动，比它小的元素一律向前移动，形成左右两个子序列，再把子序列按上述操作进行调整，直到所有的子序列中都只有一个元素时序列即为有序。

归并排序（稳定）：基本思想为：把两个或者两个以上的有序表合并成一个新的有序表。

二叉树原理？

答：（特点）二叉树是另一种树形结构，其特点是每个结点至多只有两棵子树，并且二叉树的子树有左右之分，其次序不能任意颠倒。与树相似，二叉树也以递归的形式定义。（定义）或者为空二叉树，或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。

树的应用？

答：二叉排序树、平衡二叉树、哈夫曼树。

图的应用？

答：最短路径（BFS、Dijkstra、Floyd）、最小生成树（Prim、Kruskal）、拓扑排序、关键路径。

BFS：比如现在访问起始顶点v，广度优先遍历首先是依次访问v的未访问过的邻接顶点，然后再依次访问这些邻接顶点的未访问的邻接顶点，直到所有顶点被访问过为止。如果图中尚有顶点未被访问，则另选图中未曾被访问的顶点作为起始点。（邻接矩阵 n2）

DFS：比如现在访问起始顶点v，深度优先遍历首先是访问与v邻接的但未访问过的顶点w，然后再访问与w邻接的未访问的顶点，直到所有顶点被访问过为止。如果图中尚有顶点未被访问，则另选图中未曾被访问的顶点作为起始点。（邻接表 v+e）

Dijkstra：既然解决最短路径，首先是有哪些顶点、然后是是否已找到最短路径、其次是最短路径的长度、最后是最短路径的前驱。比如源点是v0，该算法会先把v0标记为已经找到最短路径，然后将图中与其相邻且未标记为找到最短路径的顶点的距离和前驱依次记到数组中，然后找出最短路径长度数组中最小的距离，然后遍历其邻接点，再重复上述操作。（n2 不适合负权）

Floyd：初始时对图中任意两个顶点，若他们存在边，则将此边的权值作为他们之间的最短路径长度，若他们之间不存在边，则是记为无穷。然后逐步加入顶点作为中间顶点，如果增加中间顶点后，得到的路径比原来的路径长度减少了，则以此新路径代替原路径。（n3）

Prim：任取一个顶点加入树，然后每次选择一个与当前顶点集合距离最近的顶点，并将该顶点加入，直到所有顶点都加入。(n2 适合边稠密)

Kruskal：每次选择一个未被选取过且权值最小的边，若该边加入后不会形成回路，则加入，否则放弃再重新选，直到所有顶点都在一个连通分量上。(eloge 适合边稀疏而顶点多)

拓扑排序：AOV网，顶点表示活动的网络。拓扑排序有两个特点：每个顶点出现且只出现一次；若顶点A在序列中排在顶点B前面，则图中不存在从顶点B到A的路径。

关键路径：AOE网，边表示活动的网络。AOE网中仅有一个入度为0的顶点，称为源点，仅有一个出度为0的顶点，称为汇点。从源点到汇点的所有路径中，具有最大路径长度的路径称为关键路径，而关键路径上的活动称为关键活动。完成整个工程的最短时间就是关键路径的长度，若关键活动不能按时完成，则整个工程的完成时间就会延长。只要找到了关键路径，就可以得出最短完成时间。

完结，撒花。