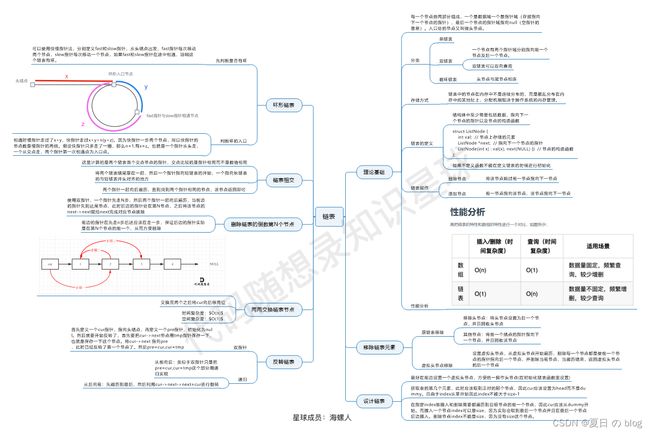
代码随想录刷题-链表总结篇

链表理论基础

单链表

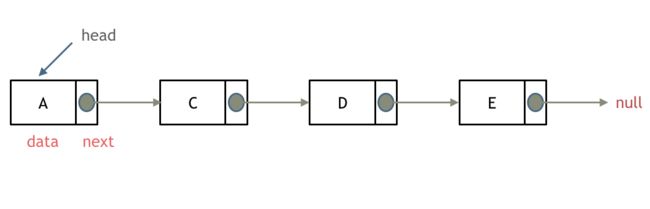
单链表是一种常见的线性数据结构，它由一系列节点组成，每个节点包含了一个数据元素和一个指向下一个节点的指针。单链表的第一个节点称为头节点，最后一个节点称为尾节点，尾节点的指针指向空地址。

单链表的优点是插入和删除操作比较快速，时间复杂度为O(1)，而查找操作则需要遍历整个链表，时间复杂度为O(n)。

代码如下：

struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数(C++11的初始化列表(initializer list)语法)
};

在实现单链表时，需要注意以下几点：

• 在插入和删除节点时，要注意更新链表中相邻节点的指针。
• 在使用完节点后，需要手动释放节点占用的内存，以避免内存泄漏的问题。
• 遍历链表时，需要使用循环结构，直到指针指向空地址。

双链表

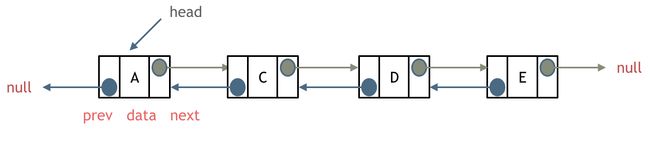
双链表中每个节点包含了一个数据元素和两个指针，分别指向前一个节点和后一个节点。双链表与单链表相比，多了一个指向前一个节点的指针，可以更方便地进行双向遍历和节点的插入和删除操作。

在C++中，可以用以下结构体定义一个双链表的结点：

struct ListNode {
    int val;              // 存储的元素值
    ListNode* prev;       // 指向前一个节点的指针
    ListNode* next;       // 指向后一个节点的指针
    ListNode(int x) : val(x), prev(nullptr), next(nullptr) {}  // 构造函数
};

循环链表

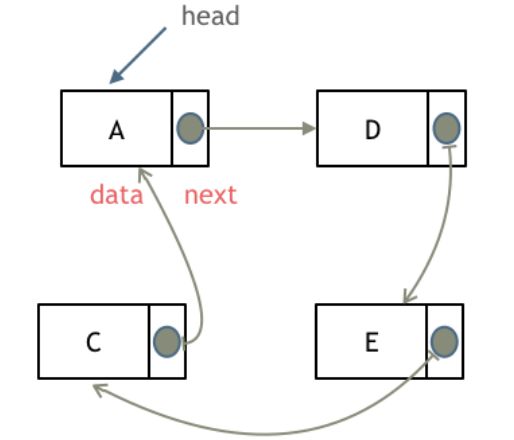
循环链表是一种特殊的链表，它的最后一个节点的下一个节点指向第一个节点，形成一个环状。循环链表可以分为单向循环链表和双向循环链表两种。

在单向循环链表中，每个节点只有一个指针，指向下一个节点。最后一个节点的指针指向第一个节点。

在双向循环链表中，每个节点有两个指针，一个指向前一个节点，一个指向后一个节点。第一个节点的前一个节点指向最后一个节点，最后一个节点的后一个节点指向第一个节点。

循环链表的优点是可以方便地实现循环遍历，因为可以从最后一个节点回到第一个节点。同时，循环链表可以解决链表中的“尾指针”问题，即在链表的末尾添加节点时不需要遍历整个链表查找最后一个节点。

但是，循环链表的缺点是实现起来比较复杂，需要特别处理最后一个节点的指针。同时，循环链表的节点数量比较难以控制，容易造成内存泄漏或者死循环等问题。

以下是一个单向循环链表的结构体：

struct ListNode {
    int val;
    struct ListNode *next;
};

struct CircularLinkedList {
    ListNode *head;
    ListNode *tail;
    int size;
};

其中，ListNode代表链表的一个节点，包含一个整数val和一个指向下一个节点的指针next。CircularLinkedList代表循环链表，包含一个指向头节点的指针head、一个指向尾节点的指针tail和链表中节点的数量size。

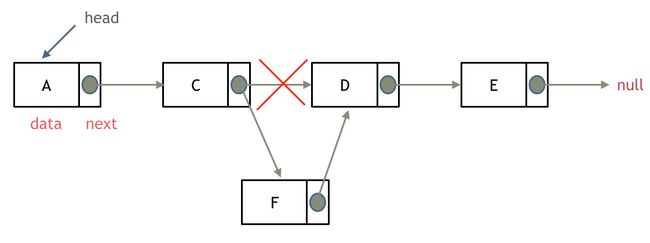
其余知识点

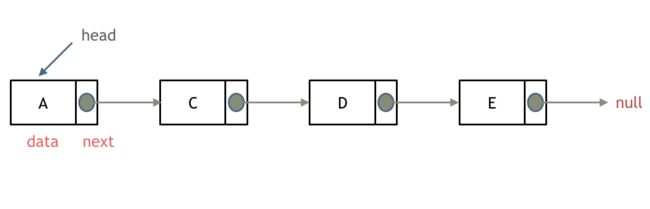
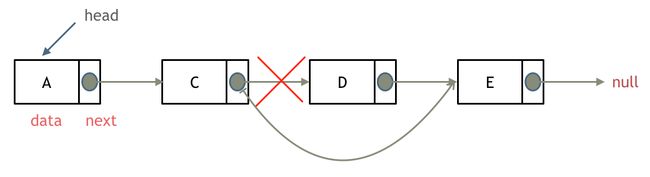
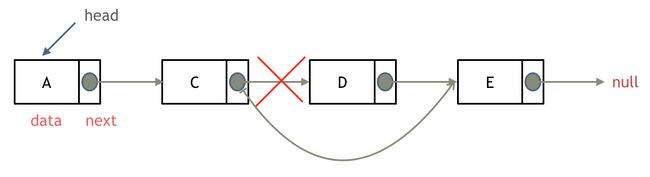
删除元素如下所示：

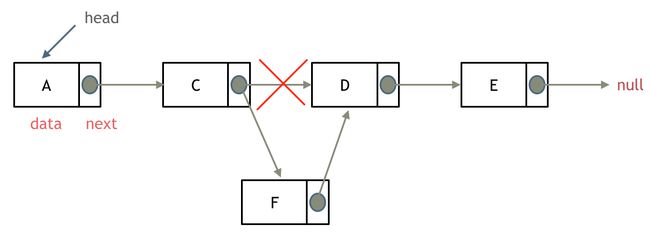
添加节点如下所示：

与顺序表对比如下：

链表理论基础

单链表

单链表是一种常见的线性数据结构，它由一系列节点组成，每个节点包含了一个数据元素和一个指向下一个节点的指针。单链表的第一个节点称为头节点，最后一个节点称为尾节点，尾节点的指针指向空地址。

单链表的优点是插入和删除操作比较快速，时间复杂度为O(1)，而查找操作则需要遍历整个链表，时间复杂度为O(n)。

代码如下：

struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数(C++11的初始化列表(initializer list)语法)
};

在实现单链表时，需要注意以下几点：

• 在插入和删除节点时，要注意更新链表中相邻节点的指针。
• 在使用完节点后，需要手动释放节点占用的内存，以避免内存泄漏的问题。
• 遍历链表时，需要使用循环结构，直到指针指向空地址。

双链表

双链表中每个节点包含了一个数据元素和两个指针，分别指向前一个节点和后一个节点。双链表与单链表相比，多了一个指向前一个节点的指针，可以更方便地进行双向遍历和节点的插入和删除操作。

在C++中，可以用以下结构体定义一个双链表的结点：

struct ListNode {
    int val;              // 存储的元素值
    ListNode* prev;       // 指向前一个节点的指针
    ListNode* next;       // 指向后一个节点的指针
    ListNode(int x) : val(x), prev(nullptr), next(nullptr) {}  // 构造函数
};

循环链表

循环链表是一种特殊的链表，它的最后一个节点的下一个节点指向第一个节点，形成一个环状。循环链表可以分为单向循环链表和双向循环链表两种。

在单向循环链表中，每个节点只有一个指针，指向下一个节点。最后一个节点的指针指向第一个节点。

在双向循环链表中，每个节点有两个指针，一个指向前一个节点，一个指向后一个节点。第一个节点的前一个节点指向最后一个节点，最后一个节点的后一个节点指向第一个节点。

循环链表的优点是可以方便地实现循环遍历，因为可以从最后一个节点回到第一个节点。同时，循环链表可以解决链表中的“尾指针”问题，即在链表的末尾添加节点时不需要遍历整个链表查找最后一个节点。

但是，循环链表的缺点是实现起来比较复杂，需要特别处理最后一个节点的指针。同时，循环链表的节点数量比较难以控制，容易造成内存泄漏或者死循环等问题。

以下是一个单向循环链表的结构体：

struct ListNode {
    int val;
    struct ListNode *next;
};

struct CircularLinkedList {
    ListNode *head;
    ListNode *tail;
    int size;
};

其中，ListNode代表链表的一个节点，包含一个整数val和一个指向下一个节点的指针next。CircularLinkedList代表循环链表，包含一个指向头节点的指针head、一个指向尾节点的指针tail和链表中节点的数量size。

其余知识点

删除元素如下所示：

添加节点如下所示：

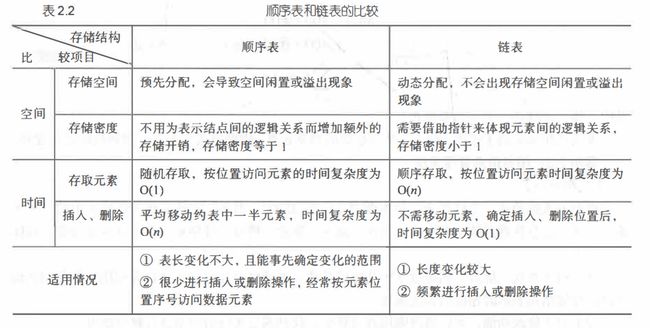
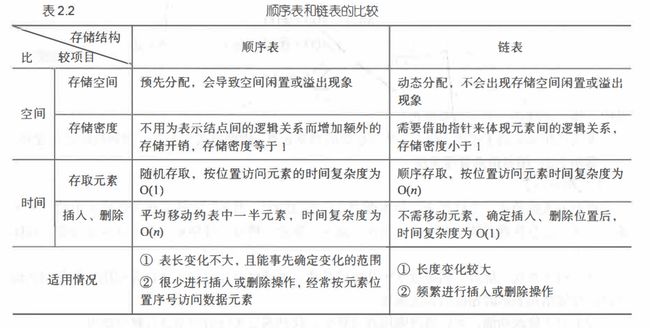
与顺序表对比如下：

移除链表元素

本节对应代码随想录中：代码随想录，讲解视频：LeetCode：203.移除链表元素_哔哩哔哩_bilibili

习题

题目链接：203.移除链表元素- 力扣（LeetCode）

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回新的头节点。

示例 1： 输入：head = [1,2,6,3,4,5,6], val = 6 输出：[1,2,3,4,5]

示例 2： 输入：head = [], val = 1 输出：[]

示例 3： 输入：head = [7,7,7,7], val = 7 输出：[]

我的解法

思路：循环判断临时指针的下一个节点值是否等于 val，等于的话就让临时指针的下一个节点指向为临时指针的下下个节点，否则就让临时指针指向下一个节点(相当于遍历)。但是这种方法是判断的下一个节点，因此要单独判断头结点的情况，同时注意要使用 while 而不是 if，因为用 if 有可能删了等于 val 的头结点，下一个节点依然等于 val。

class Solution {
   public:
    ListNode* removeElements(ListNode* head, int val) {
        // 处理特殊情况
        if (head == nullptr){
            return nullptr;  
        }
     
        // 判断首个元素等于val的情况        
        while(head->val == val){
            head = head->next;
            // 如果head已经是nullptr说明已经没元素了,直接返回nullptr
            if(head == nullptr){
                return nullptr;
            }     
        }
        ListNode* temp = head;
        // 判断的是temp的下一个元素,因此上面要加上判断首个元素的情况
        while (temp->next != nullptr) {
            // 如果下一个元素值为val,则让temp的下一个元素等于下下个元素
            if(temp->next->val==val){
                temp->next=temp->next->next;
            }else{
                // 否则temp等于下一个元素(相当于遍历单链表)
                temp = temp->next;
            }
        }
        return head;
    }
};

• 时间复杂度：O(n)。这段代码中使用了一个while循环来遍历单链表，每次循环中都会判断当前节点的下一个节点是否需要删除，循环的次数是单链表的长度n，因此时间复杂度是O(n)。
• 空间复杂度：O(1)。这段代码中只使用了常量级别的额外空间，因此空间复杂度是O(1)。

需要注意的事项：

• 注意在 C++中删除节点后要用 delete 手动删除这个节点的内存空间

虚拟头结点解法

上面我用的解法，由于头结点和其余节点情况不一致(头节点前面没有元素，用 next 的方式无法判断头结点)，所以需要单独判断头结点。而我们可以在头结点前面加上一个虚拟节点，指向头节点，这样虚拟节点的 next 就指向了头节点，从而实现头结点和其余节点处理逻辑达到一致。

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向head，这样方面后面做删除操作
        ListNode* cur = dummyHead; // 临时指针
        while (cur->next != NULL) {
            if(cur->next->val == val) {
                ListNode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp; // 别忘了删除内存
            } else {
                cur = cur->next;
            }
        }
        head = dummyHead->next; // 返回的是虚拟头节点的下一个节点(原始的头节点)
        delete dummyHead;
        return head;
    }
};

• 时间复杂度：O(n)。这段代码中使用了一个while循环来遍历单链表，每次循环中都会判断当前节点的下一个节点是否需要删除，循环的次数是单链表的长度n，因此时间复杂度是O(n)。
• 空间复杂度：O(1)。这段代码中只使用了常量级别的额外空间，因此空间复杂度是O(1)。

设计链表

本节对应代码随想录中：代码随想录，讲解视频：帮你把链表操作学个通透！LeetCode：707.设计链表_哔哩哔哩_bilibili

习题

题目链接：707. 设计链表 - 力扣（LeetCode）

设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性：val 和 next。val 是当前节点的值，next 是指向下一个节点的指针/引用。如果要使用双向链表，则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。

在链表类中实现这些功能：

• get(index)：获取链表中第 index 个节点的值。如果索引无效，则返回-1。
• addAtHead(val)：在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
• addAtTail(val)：将值为 val 的节点追加到链表的最后一个元素。
• addAtIndex(index,val)：在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果index小于0，则在头部插入节点。
• deleteAtIndex(index)：如果索引 index 有效，则删除链表中的第 index 个节点。

示例：

MyLinkedList linkedList = new MyLinkedList();
linkedList.addAtHead(1);
linkedList.addAtTail(3);
linkedList.addAtIndex(1,2); //链表变为1-> 2-> 3
linkedList.get(1); //返回2
linkedList.deleteAtIndex(1); //现在链表是1-> 3
linkedList.get(1); //返回3

我的解法

题意很直接，就是链表的常见操作。但刚开始写的时候不太明白 class 里面怎么放头节点，看了代码随想录部分题解才明白在 class 里放一个节点的 struct 就可以。同样这题在头节点前加上一个虚拟头节点会更方便点。

注意下插入节点赋值 next 时的先后顺序，如1 3中间插入2，先让节点2的 next 等于节点1的 next，再让节点1的 next 等于节点2。如果顺序反了的话，先让节点1的 next 等于节点2，这样节点2的 next 就找不到节点3了。

class MyLinkedList {
   public:
    struct Node {
        int val;
        Node* next;
        Node(int data) : val(data), next(nullptr) {}
    };
    // 初始化虚拟头节点，设置长度为0
    MyLinkedList() {
        fakeNode = new Node(0);
        size = 0;
    }
    
    int get(int index) {
        // 虽然通过了LeetCode，但这里没判断index<0的情况，要加上
        if (index + 1 > size) {
            return -1;
        }
        Node* tmp = fakeNode;
        for (int i = 0; i < index + 1; i++) {
            tmp = tmp->next;
        }
        // 遍历后tmp就是index位置的节点
        return tmp->val;
    }

    void addAtHead(int val) {
        Node* newNode = new Node(val);
        // 必须先设置newNode的next，否则就找不到真正的头节点了
        newNode->next = fakeNode->next;
        fakeNode->next = newNode;
        size++;
    }

    void addAtTail(int val) {
        Node* tmp = fakeNode;
        Node* newNode = new Node(val);
        for (int i = 0; i < size; i++) {
            tmp = tmp->next;
        }
        tmp->next = newNode;
        size++;
    }

    void addAtIndex(int index, int val) {
        if (index > size) {
            return;
        }
        if (index < 0) {
            addAtHead(val);
            return;
        }
        Node* newNode = new Node(val);
        Node* tmp = fakeNode;
        for (int i = 0; i < index; i++) {
            tmp = tmp->next;
        }
        // 遍历后tmp位于index的前一个位置
        newNode->next = tmp->next;
        tmp->next = newNode;
        size++;
    }

    void deleteAtIndex(int index) {
        // 还是没判断index<0的情况，要加上
        if (index + 1 > size) {
            return;
        }
        Node* tmp = fakeNode;
        for (int i = 0; i < index; i++) {
            tmp = tmp->next;
        }
        // 遍历后tmp位于index的前一个位置
        Node* deleteNode = tmp->next;
        tmp->next = tmp->next->next;
        delete deleteNode;  // 手动删除节点内存
        size--;
    }

    void printNode() {
        Node* tmp = fakeNode;
        for (int i = 0; i < size; i++) {
            tmp = tmp->next;
            cout << tmp->val;
        }
    }

   private:
    Node* fakeNode;
    int size;
};

• 时间复杂度分析
  • get(int index)：时间复杂度为 O(n)，因为需要遍历整个链表，找到 index 位置的节点。
  • addAtHead(int val)：时间复杂度为 O(1)，因为只需要修改头节点的指向，不需要遍历整个链表。
  • addAtTail(int val)：时间复杂度为 O(n)，因为需要遍历整个链表，找到尾节点，并在其后面添加新节点。
  • addAtIndex(int index, int val)：时间复杂度为 O(n)，因为需要遍历整个链表，找到 index 位置的前一个节点，并在其后面添加新节点。
  • deleteAtIndex(int index)：时间复杂度为O(n)，因为需要遍历整个链表，找到index位置的前一个节点，并删除其后面的节点。
• 空间复杂度：O(n)。这段代码中使用了一个结构体Node来表示单链表的节点，以及一个指向虚拟头节点的指针fakeNode和一个记录链表长度的变量size。其中，节点的数量和虚拟头节点的数量都是n+1个，因此空间复杂度是O(n)。

需要注意的点如下：

• 注意 index 的极端情况，本题我就没判断 index<0的情况，虽然通过了测试用例，但严格意义上并不全对
• 代码中的 size 和 fakeNode 前面加个 _ 更好，如 _size ，这样能和其他变量区分，当然也可以用 this->size

代码随想录代码

和我的代码类似，我用的 for 循环遍历，他用的 while 遍历。注释已经很清晰了，就不过多讲解了。

class MyLinkedList {
public:
    // 定义链表节点结构体
    struct LinkedNode {
        int val;
        LinkedNode* next;
        LinkedNode(int val):val(val), next(nullptr){}
    };

    // 初始化链表
    MyLinkedList() {
        _dummyHead = new LinkedNode(0); // 这里定义的头结点 是一个虚拟头结点，而不是真正的链表头结点
        _size = 0;
    }

    // 获取到第index个节点数值，如果index是非法数值直接返回-1， 注意index是从0开始的，第0个节点就是头结点
    int get(int index) {
        if (index > (_size - 1) || index < 0) {
            return -1;
        }
        LinkedNode* cur = _dummyHead->next;
        while(index--){ // 如果--index 就会陷入死循环
            cur = cur->next;
        }
        return cur->val;
    }

    // 在链表最前面插入一个节点，插入完成后，新插入的节点为链表的新的头结点
    void addAtHead(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        newNode->next = _dummyHead->next;
        _dummyHead->next = newNode;
        _size++;
    }

    // 在链表最后面添加一个节点
    void addAtTail(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(cur->next != nullptr){
            cur = cur->next;
        }
        cur->next = newNode;
        _size++;
    }

    // 在第index个节点之前插入一个新节点，例如index为0，那么新插入的节点为链表的新头节点。
    // 如果index 等于链表的长度，则说明是新插入的节点为链表的尾结点
    // 如果index大于链表的长度，则返回空
    // 如果index小于0，则在头部插入节点
    void addAtIndex(int index, int val) {

        if(index > _size) return;
        if(index < 0) index = 0;        
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
        _size++;
    }

    // 删除第index个节点，如果index 大于等于链表的长度，直接return，注意index是从0开始的
    void deleteAtIndex(int index) {
        if (index >= _size || index < 0) {
            return;
        }
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur ->next;
        }
        LinkedNode* tmp = cur->next;
        cur->next = cur->next->next;
        delete tmp;
        _size--;
    }

    // 打印链表
    void printLinkedList() {
        LinkedNode* cur = _dummyHead;
        while (cur->next != nullptr) {
            cout << cur->next->val << " ";
            cur = cur->next;
        }
        cout << endl;
    }
private:
    int _size;
    LinkedNode* _dummyHead;

};

• 时间复杂度和空间复杂度同上

反转链表

本节对应代码随想录中：代码随想录，讲解视频：帮你拿下反转链表 | LeetCode：206.反转链表 | 双指针法 | 递归法_哔哩哔哩_bilibili

习题

题目链接：206. 反转链表 - 力扣（LeetCode）

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例：
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

双指针

例如，上面的示例，我们想反转 1 2 3 4 5。用一个指针 cur 用来遍历单链表，再用另一个指针 pre 指向 cur 的前面一个节点。例如 cur=2时，原本是1->2，现在要变成2->1。直接让 cur->next=pre 就可以实现，但这样的话，后面的3就没法遍历到了。所以要用一个临时指针 temp 先指向 cur->next，再让 cur->next=pre。

到这里，就实现了1和2的反转，如果想继续遍历下去，还需让 pre 和 cur 都向后移一位。现在 pre、cur 和 temp 的位置为：pre cur temp，要让 pre 和 cur 向后移一位，只要让 pre=cur，cur=temp 即可。注意这两个顺序不能颠倒，否则 cur 先等于 temp，那就相当于丢失了原来的 cur。

class Solution {
   public:
    ListNode* reverseList(ListNode* head) {
        ListNode* cur = head;
        ListNode* pre = nullptr;
        ListNode* tmp;
        while (cur != nullptr) {
            tmp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
};

• 时间复杂度：O(n)。其中n为链表的长度。因为算法需要遍历整个链表，时间复杂度与链表长度成正比。
• 空间复杂度：O(1)。因为算法只使用了常数级别的额外空间，即三个指针变量。无论输入的链表有多长，算法所需的额外空间都是固定的，与链表长度无关。

递归

首先给出代码随想录上类似双指针的递归。新定义了一个函数，将初始化的步骤更改为传参给新定义的函数来实现，而将两个指针后移的步骤更改为调用函数递归来实现。同时，和双指针的结束条件一样，cur == NULL 时递归函数结束。

class Solution {
public:
    ListNode* reverse(ListNode* pre,ListNode* cur){
        if(cur == NULL) return pre;
        ListNode* temp = cur->next;
        cur->next = pre;
        // 可以和双指针法的代码进行对比，如下递归的写法，其实就是做了这两步
        // pre = cur;
        // cur = temp;
        return reverse(cur,temp);
    }
    ListNode* reverseList(ListNode* head) {
        // 和双指针法初始化是一样的逻辑
        // ListNode* cur = head;
        // ListNode* pre = NULL;
        return reverse(NULL, head);
    }

};

• 时间复杂度：O(n)。其中n为链表的长度。因为算法需要遍历整个链表，时间复杂度与链表长度成正比。
• 空间复杂度：O(n)。因为算法使用了递归操作，递归深度最多为n层，每层递归需要保存当前节点的指针以及前一个节点的指针，因此空间复杂度为O(n)。

上面的递归由于和双指针的写法类似，还较为容易理解，而LeetCode 官方给出了更简洁的递归。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (!head || !head->next) {
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }
};

评论区有人给出了详细的注释(java 版本)。对于 head->next->next = head;，如 1 2 3，head=2，head->next=3，3->next=2，相当于2<->3。但是反转后2的 next 不应该再指向3了，因此 head->next = nullptr; 将2的 next 置为 nullptr。

public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            /*
                直到当前节点的下一个节点为空时返回当前节点
                由于5没有下一个节点了，所以此处返回节点5
             */
            return head;
        }
        //递归传入下一个节点，目的是为了到达最后一个节点
        ListNode newHead = reverseList(head.next);
                /*
            第一轮出栈，head为5，head.next为空，返回5
            第二轮出栈，head为4，head.next为5，执行head.next.next=head也就是5.next=4，
                      把当前节点的子节点的子节点指向当前节点
                      此时链表为1->2->3->4<->5，由于4与5互相指向，所以此处要断开4.next=null
                      此时链表为1->2->3->4<-5
                      返回节点5
            第三轮出栈，head为3，head.next为4，执行head.next.next=head也就是4.next=3，
                      此时链表为1->2->3<->4<-5，由于3与4互相指向，所以此处要断开3.next=null
                      此时链表为1->2->3<-4<-5
                      返回节点5
            第四轮出栈，head为2，head.next为3，执行head.next.next=head也就是3.next=2，
                      此时链表为1->2<->3<-4<-5，由于2与3互相指向，所以此处要断开2.next=null
                      此时链表为1->2<-3<-4<-5
                      返回节点5
            第五轮出栈，head为1，head.next为2，执行head.next.next=head也就是2.next=1，
                      此时链表为1<->2<-3<-4<-5，由于1与2互相指向，所以此处要断开1.next=null
                      此时链表为1<-2<-3<-4<-5
                      返回节点5
            出栈完成，最终头节点5->4->3->2->1
         */
        head.next.next = head;
        head.next = null;
        return newHead;
    }

如果还是觉得有点抽象不太好理解，可以看下这个视频讲解：链表反转(递归法)_哔哩哔哩_bilibili

两两交换链表中的节点

本节对应代码随想录中：代码随想录，讲解视频：帮你把链表细节学清楚！ | LeetCode：24. 两两交换链表中的节点_哔哩哔哩_bilibili

习题

题目链接：24. 两两交换链表中的节点 - 力扣（LeetCode）

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

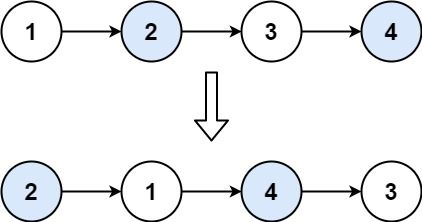
输入：head = [1,2,3,4]
输出：[2,1,4,3]

我的解法

由于上面的反转链表用了双指针，这题我首先想到的是用双指针的解法。定义一个虚拟头节点。

对于0 1 2 3 4，cur 指针指向1也就是待交换的两个节点中的第一个节点，由于交换后1前面的0的 next 也会改变，所以我的想法是定义第二个指针 pre 用来记录 cur 前面的节点。

定义一个临时指针等于 cur 的 next 即2，然后就是1.next=3、2.next=1、0.next=2，如果不用临时指针保存2，那么1.next=3时就无法找到2了。

交换后顺序为0 2 1 3 4，此时 pre 还是指向0，cur 指向2。cur=cur->next 即可让 cur 遍历到下一个待交换元素的第一个位置，而在这之前首先让 pre=cur 先让 pre 前进到下一个待交换元素的前一个。

而 while 循环的终止条件，每次 cur 都会指向的是待交换元素的第一个。如果是偶数个那么 cur 为 nullptr，如果是奇数个，那么 cur->next 为 nullptr。

一顿 next 操作后很可能就会有点迷，只要记住 cur 和 pre 这些都是指针，它们记录的是地址，不管你再怎么 next 操作，地址中的值都没发生变化。也就是说，刚开始0 1 2 3 4，cur 指向的是1，交换操作后变成0 2 1 3 4，此时 cur 指向的还是1。因此如果想让 cur 指向3只需让 cur=cur->next 即可。

class Solution {
   public:
    ListNode* swapPairs(ListNode* head) {
        
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;

        ListNode* pre = dummyHead;//0
        ListNode* cur = head; //1
        // 0 1 2 3
        while (cur != nullptr && cur->next != nullptr) {
            ListNode* next_tmp = cur->next;//2
            cur->next = next_tmp->next;//1.next=3
            next_tmp->next = cur;//2.next=1
            pre->next = next_tmp;//0.next=2

            pre = cur;
            cur = cur->next;
        }

        return dummyHead->next;
    }
};

• 时间复杂度：O(n)。其中n为链表的长度。因为算法需要遍历整个链表，时间复杂度与链表长度成正比。
• 空间复杂度：O(1)。因为算法只使用了常数级别的额外空间，即三个指针变量和一个虚拟头节点。无论输入的链表有多长，算法所需的额外空间都是固定的，与链表长度无关。

代码随想录解法

在我的解法中，使用了双指针和一个临时指针变量。而在代码随想录中，作者使用了一个指针，两个临时指针变量。

Carl 的解法中 cur 指向的是待交换节点的前一个节点，交换顺序如下图所示。执行步骤一后，节点1就没法找到，所以用一个临时节点记录节点1。执行步骤2后，节点3就没法找到，所以再用一个临时变量记录节点3。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WNQIxCg5-1679135679524)(https://code-thinking.cdn.bcebos.com/pics/24.%E4%B8%A4%E4%B8%A4%E4%BA%A4%E6%8D%A2%E9%93%BE%E8%A1%A8%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B91.png)]

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向head，这样方面后面做删除操作
        ListNode* cur = dummyHead;
        while(cur->next != nullptr && cur->next->next != nullptr) {
            ListNode* tmp = cur->next; // 记录临时节点 1
            ListNode* tmp1 = cur->next->next->next; // 记录临时节点 3

            cur->next = cur->next->next;    // 步骤一 0.next=2
            cur->next->next = tmp;          // 步骤二 2.next=1
            cur->next->next->next = tmp1;   // 步骤三 1.next=3

            cur = cur->next->next; // cur移动两位，准备下一轮交换
        }
        return dummyHead->next;
    }
};

• 时间复杂度：O(n)。其中n为链表的长度。因为算法需要遍历整个链表，时间复杂度与链表长度成正比。
• 空间复杂度：O(1)。因为算法只使用了常数级别的额外空间，即四个指针变量和一个虚拟头节点。无论输入的链表有多长，算法所需的额外空间都是固定的，与链表长度无关。

但其实这里只用一个指针就可以，还是上面的例子，0 1 2 3 4。Carl 的解法中 cur 指向0，定义了两个临时变量分别保存1和3，但其实只需要一个临时变量保存2即可。

为什么保存2可以只用一个临时变量呢？我们知道转换后是0 2 1 3，再看三个步骤的顺序。

1.next=3、2.next=1、0.next=2，刚好是转换后的顺序从后往前，而 Carl 的顺序是从前往后。由于单链表只有向后 next 的顺序，从前往后的话，前面的 next 值都变了，就会失去更多原有可以根据 next 找到的值。执行1.next=3后，由于原本2可以通过1.next 找到，现在1.next=3了，所以就需要一个临时变量来保存2。

// cur:0
// 0 1 2 3 4
ListNode* tmp = cur->next->next;  // 记录临时节点2
cur->next->next = tmp->next;      // 步骤一 1.next=3
tmp->next = cur->next;            // 步骤二 2.next=1
cur->next = tmp;                  // 步骤三 0.next=2

删除链表的倒数第N个节点

本节对应代码随想录中：代码随想录，讲解视频：链表遍历学清楚！ | LeetCode：19.删除链表倒数第N个节点_哔哩哔哩_bilibili

习题

题目链接：19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cNZhXKXu-1679135703683)(null)]

• 输入：head = [1,2,3,4,5], n = 2；输出：[1,2,3,5]
• 输入：head = [1], n = 1；输出：[]
• 输入：head = [1,2], n = 1；输出：[1]

直观解法

这道题目还挺简单的，题意也很明确。需要注意的是最好使用虚拟头结点，否则示例2这种就需要单独处理会麻烦一点。比较容易想到的就是既然要删倒数第 n 个节点，那我们首先遍历以下链表看看总共有多少个节点，然后再根据总节点数量 size 和 n 的大小遍历到待删节点的前一个节点执行删除操作即可。

这里需要注意的就是遍历的边界条件是到了待删节点的前一个节点开始执行删除操作。当遍历到待删节点本身的时候是无法进行删除的，因为我们无法获得待删节点的前一个节点是什么。

class Solution {
   public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* tmp = head;
        int size = 0;   // 记录链表长度
        // 计算链表长度
        while (tmp != nullptr) {
            tmp = tmp->next;
            size++;
        }
        tmp = dummyHead;
        // 找到待删除节点的前一个节点
        for (int i = 0; i < size - n; i++) {
            tmp = tmp->next;
        }
        ListNode* delNode = tmp->next;
        tmp->next = tmp->next->next;
        delete delNode;
        return dummyHead->next;
    }
};

• 时间复杂度：O(n)。其中n为链表的长度。因为算法需要遍历整个链表两次，时间复杂度与链表长度成正比。
• 空间复杂度：O(1)。因为算法只使用了常数级别的额外空间，即三个指针变量和一个虚拟头节点。无论输入的链表有多长，算法所需的额外空间都是固定的，与链表长度无关。

可以优化的点：

• 今天看官方题解突然发现 ListNode* dummyHead = new ListNode(0);dummyHead->next = head; 这两句其实可以用 ListNode* dummyHead = new ListNode(0, head); 这一句话来实现。因为 ListNode 的构造函数中有这样一句 ListNode(int x, ListNode *next) : val(x), next(next) {} 可以直接指定节点的 next，不过写成两句更加直观一点。

双指针

LeetCode 上题目描述中进阶中说“你能尝试使用一趟扫描实现吗？”。一开始没想出来，看了题目的提示：Maintain two pointers and update one with a delay of n steps.才明白。

例如0 1 2 3 4 5，我们可以用一个指针 cur 来遍历，用另一个指针 pre 慢 cur 指针 n+1 步遍历。比如 n=2时，当 cur=3时，pre=0(虚拟头结点)，然后两个指针一起移动，当 cur 遍历到5后面的 nullptr 时，pre 刚好遍历到待删节点4的前一个节点3的位置。

如果是慢 n 步遍历，那么 pre 会遍历到待删节点4的位置，此时是无法执行删除节点4的操作的，因此是慢 n+1步。

class Solution {
   public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyNode = new ListNode(0);
        dummyNode->next = head;
        ListNode* cur = dummyNode;
        ListNode* pre = dummyNode;
        // cur先向前移动n+1步
        for (int i = 0; i < n + 1; i++) {
            cur = cur->next;
        }
        // 然后cur和pre一起向前移动
        while (cur != nullptr) {
            cur = cur->next;
            pre = pre->next;
        }
        ListNode* delNode = pre->next;
        pre->next = pre->next->next;
        delete delNode;
        return dummyNode->next;
    }
};

• 时间复杂度：O(n)。其中n为链表的长度。因为算法需要遍历整个链表一次，时间复杂度与链表长度成正比。
• 空间复杂度：O(1)。因为算法只使用了常数级别的额外空间，即三个指针变量和一个虚拟头节点。无论输入的链表有多长，算法所需的额外空间都是固定的，与链表长度无关。

但是写完之后又有点疑惑，这还算是一趟扫描吗，因为其中有 for 循环和 while 循环。仔细琢磨后发现确实算是一趟扫描。

直观解法的解法中，在第一趟扫描中，需要计算链表的长度，以便确定需要删除节点的前一个节点。而在第二趟扫描中，才真正开始删除节点。因此，这个解法需要进行两趟扫描。而双指针解法使用了两个指针来记录待删除节点的前一个节点，而不需要事先计算链表的长度。

举个极端点的例子，在1000个节点中，我想删除倒数第1个节点即节点1000，在第一个解法中，需要先遍历1000个节点得知链表长度为1000，然后再遍历一趟到节点999的位置执行删除操作。而在第二个解法中，只需要 cur 指针先向前走2步，然后 pre 指针和 cur 指针再开始一起走，最后 cur 指针走到节点1000的下一个即 nullptr 时，pre 刚好走到节点999的位置。在这个例子中，解法一走了1001+999=1999步，而解法二只走了1001+2=1003步！

为什么是1001而不是1000？因为从1000走到下一步 nullptr 还需要一步

如果你还是有点不太理解，看看下面的代码，它没有使用 for 循环而是使用了 size 进行计数，其实和上面的解法是一个意思。

class Solution {
   public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* cur = dummyHead;
        ListNode* pre = dummyHead;
        int size = 0;
        while (cur != nullptr) {
            // size > n说明慢指针可以开始移动了
            if (size > n)
                // 循环结束后pre指向待删除节点的前一个节点
                pre = pre->next;
            else
                size++;
            cur = cur->next;
        }
        ListNode* delNode = pre->next;
        pre->next = pre->next->next;
        delete delNode;
        return dummyHead->next;
    }
};

• 时间复杂度：O(n)。其中n为链表的长度。因为算法需要遍历整个链表一次，时间复杂度与链表长度成正比。
• 空间复杂度：O(1)。因为算法只使用了常数级别的额外空间，即三个指针变量和一个虚拟头节点。无论输入的链表有多长，算法所需的额外空间都是固定的，与链表长度无关。

相交链表

本节对应代码随想录中：代码随想录，暂无讲解视频

习题

题目链接：160. 相交链表 - 力扣（LeetCode）

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

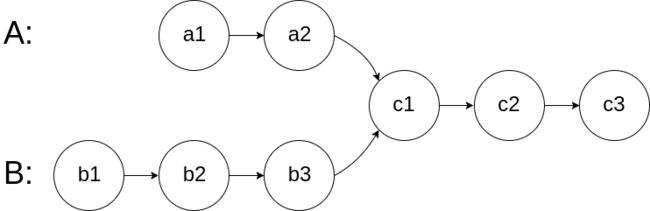
图示两个链表在节点 c1 开始相交：

题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须保持其原始结构。

自定义评测：
评测系统的输入如下（你设计的程序不适用此输入）：

• intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
• listA - 第一个链表
• listB - 第二个链表
• skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
• skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数
  评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被视作正确答案。

示例 1：

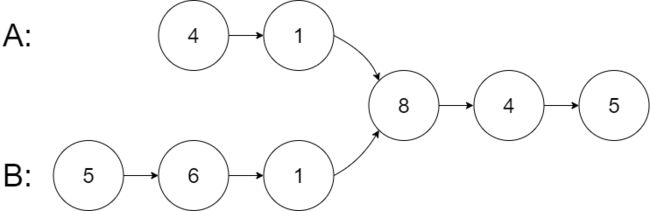
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at ‘8’
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

进阶：你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

题目说明

相信会有不少小伙伴看到题目会有点疑惑，尤其是在代码随想录中跳转到的 面试题 02.07. 链表相交 - 力扣（LeetCode） 这个题目，两个题是一样的，只不过 160. 相交链表 - 力扣（LeetCode）的题目描述更加清楚。

上面的示例，不少人刚看到会疑惑为什么相交的节点不是1？而是8。注意题目中说的是节点相同，示例中 A 的1和 B 的1是地址不一样，只不过两个地址的数值是一样的。比如 A 中的节点1的地址0x1111，而 B 中的节点1的地址为0x2222。A 中的节点4的 next 指向的是地址为0x1111的数值为1的节点，而 B 中的节点6的 next 指向的是地址为0x2222的数值为1的节点。而节点8是两个链表相交的节点，因为两个链表中节点8的地址是一样的。

至于怎么判断两个节点是否相同，只需判断两个指针是否相同即可，如 curA==curB，如果你用 curA->val==curB->val 进行判断就会导致上面的例子程序输出1而不是正确答案8。

并且在本地的代码和官方的评测系统是不一样的，就是说你创建了上面示例的两个链表，数值相同的节点地址不一定是相同的，而评测系统根据 skipA 和 skipB 参数会找到正确的结果。因此在本地运行极有可能得不到正确答案，要在评测系统上提交才行。

暴力解法

这种解法简单粗暴，既然要判断是否有相交的节点。那我们直接遍历链表 A 的每个节点，对于每个节点，分别遍历 B 中的各个节点看看是否有和当前节点相同的节点，只要相同，说明后续节点肯定都一样，直接返回当前节点即可。

curA == curB 说明节点相同，并且地址也相同，那么 curA 和 curB 的后续 next 肯定都相同

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        while(curA!=nullptr){
            curB = headB;
            while(curB!=nullptr){
                if(curA == curB){
                    return curA;
                }
                curB = curB->next;
            }
            curA = curA->next;
        }
        return nullptr;
    }
};

• 时间复杂度：O(mn)。其中m和n分别为链表headA和headB的长度。因为算法需要遍历headA和headB中的所有节点，时间复杂度与链表长度成正比。
• 空间复杂度：O(1)。因为算法只使用了常数级别的额外空间，即两个指针变量。无论输入的链表有多长，算法所需的额外空间都是固定的，与链表长度无关。

进阶解法

如图，如果两个链表相交，那么它们的后面几个节点一定是相同的。那么我们就可以先让节点数多的那个链表向后移动两个链表节点数量的差值。在下图中就是 B 中的指针 curB 先移动到 b2位置，curA 指针指向 a1，然后两个指针每次都向后移动一个位置，判读两个指针是否相等。当相等的时候，说明节点相同，返回当前指针。

代码如下，大致思路就是先计算两个链表的长度，然后将两个指针分别向后移动对应的步数(节点数少的移动步数为0)，最后 while 循环判断指针是否相等，不等就分别向后移动一个位置。

class Solution {
   public:
    ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
        int sizeA = 0, sizeB = 0;
        ListNode* dummyHeadA = new ListNode(0,headA);
        ListNode* dummyHeadB = new ListNode(0,headB);
        ListNode* curA = dummyHeadA;
        ListNode* curB = dummyHeadB;
        // 计算两个单链表的长度，循环结束后curA和curB指向的是各自链表最后一个节点
        while (curA->next != nullptr) {
            curA = curA->next;
            sizeA++;
        }
        while (curB->next != nullptr) {
            curB = curB->next;
            sizeB++;
        }
        // 如果两个链表的最后一个节点不同，说明一定没有相交的节点
        if (curA != curB)
            return nullptr;
        curA = headA;
        curB = headB;
        // 计算两个指针移动的步数
        int moveA = sizeA > sizeB ? sizeA - sizeB : 0;
        int moveB = sizeB > sizeA ? sizeB - sizeA : 0;
        // 两个指针分别移动各自的步数
        for (int i = 0; i < moveA; i++)
            curA = curA->next;
        for (int i = 0; i < moveB; i++)
            curB = curB->next;
        // 开始向后遍历，当两个节点相同时则返回
        while (curA != nullptr) {
            if (curA == curB) {
                return curA;
            }
            curA = curA->next;
            curB = curB->next;
        }
        return nullptr;
    }
};

• 时间复杂度：O(m+n)。其中m和n分别为链表headA和headB的长度。因为算法需要遍历headA和headB中的所有节点，时间复杂度与链表长度成正比。
• 空间复杂度：O(1)。因为算法只使用了常数级别的额外空间，即四个指针变量和两个虚拟头节点。无论输入的链表有多长，算法所需的额外空间都是固定的，与链表长度无关。

双指针解法

该双指针解法来源于 LeetCode 官方题解：相交链表 - 相交链表 - 力扣（LeetCode）。和上面的进阶解法其实是一个思路，只不过官方的题解太简洁了！

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if (headA == nullptr || headB == nullptr) {
            return nullptr;
        }
        ListNode *pA = headA, *pB = headB;
        while (pA != pB) {
            pA = pA == nullptr ? headB : pA->next;
            pB = pB == nullptr ? headA : pB->next;
        }
        return pA;
    }
};

• 时间复杂度：O(m+n)。其中m和n分别为链表headA和headB的长度。因为算法需要遍历headA和headB中的所有节点，时间复杂度与链表长度成正比。
• 空间复杂度：O(1)。因为算法只使用了常数级别的额外空间，即两个指针变量。无论输入的链表有多长，算法所需的额外空间都是固定的，与链表长度无关。

首先，判断了特殊情况，即链表 headA 或链表 headB 为空的情况，如果其中一个链表为空，则说明它们没有相交节点，直接返回 nullptr。

接着，定义了两个指针 pA 和 pB，分别指向链表 headA 和链表 headB 的头节点。

然后，代码进入循环，判断 pA 和 pB 是否指向同一个节点，如果不是则继续循环。在循环中，pA 和 pB 分别向后移动一个节点，如果移动到链表的末尾，则将其指向另一个链表的头节点，这样可以保证两个指针同时遍历链表 headA 和链表 headB，直到找到相交节点或者遍历完所有节点。

最后，代码返回 pA 或 pB，因为它们指向的是相交节点。如果没有相交节点，则返回 nullptr。

其中的 pA = pA == nullptr ? headB : pA->next; 可以写成如下代码：

if (pA == nullptr) {
    pA = headB;
} else {
    pA = pA->next;
}

至于为什么遍历完自己的链表后将指针指向另一个链表的头部就能同时到达相交的节点，理由如下：

链表 headA 和 headB 的长度分别是 m 和 n。假设链表 headA 的不相交部分有 a 个节点，链表 headB 的不相交部分有 b 个节点，两个链表相交的部分有 c 个节点，则有 a+c=m， b+c=n。

指针 pA 会遍历完链表 headA，指针 pB 会遍历完链表 headB，两个指针不会同时到达链表的尾节点，然后指针 pA 移到链表 headB 的头节点，指针 pB 移到链表 headA 的头节点，然后两个指针继续移动，在指针 pA 移动了 a+c+b 次、指针 pB 移动了 b+c+a 次之后，两个指针会同时到达两个链表相交的节点，该节点也是两个指针第一次同时指向的节点，此时返回相交的节点。

如果链表不相交，在指针 pA 移动了 m+n 次、指针 pB 移动了 n+m 次之后，两个指针会同时变成空值 null，此时返回 null。也就是说两个指针都最多走 m+n 次。

理由解释来自 LeetCode 官方

举个例子，链表 headA 的节点为 1 2 7 8，链表 headB 的节点为 4 5 6 7 8。则 a = 2,b=3,c=2。

• PA 指向 headA 的8时，PB 指向 headB 的7。
• 然后 PA 指向 headB 的头结点级4，PB 指向 headB 的8。
• 然后 PA 指向 headB 的5，PB 指向 headA 的1。
• 然后 PA 指向 headB 的6，PB 指向 headA 的2。
• 然后 PA 指向 headB 的7，PB 指向 headA 的7。
• 两个节点相同，返回 PA。

PA 走了 a+c+b=2+2+3=7步，PB 走了 b+c+a=3+2+2=7步，然后剩余的链表都还有 c=2步没有走。为什么剩余的都是 c 步？因为两个指针都最多走 m+n 次即 a+c+b+c 步。虽然 PA 和 PB 走的顺序不一样但都把前面的 abc 走了，只剩下最后的 c 步了。

环形链表 II

本节对应代码随想录中：代码随想录，讲解视频：把环形链表讲清楚！ 如何判断环形链表？如何找到环形链表的入口？ LeetCode：142.环形链表II_哔哩哔哩_bilibili

习题

题目链接：142. 环形链表 II - 力扣（LeetCode）

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改链表。

示例 1：

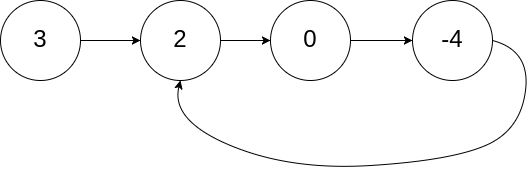
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

进阶：你是否可以使用 O(1) 空间解决此题？

我的解法

非最优解，只是个人解法记录

我的想法是遍历每个节点，并且用 now 记录虚拟头节点到当前节点的距离，同时用 last 记录上一个 now 值。对于每个节点从头节点向后遍历，比较 now 和 last。

当出现环的时候，比如上图的3 2 0 -4，cur 指向-4时，虚拟头结点到-4的距离为4，当遍历下一个节点即2时，虚拟头结点到2的距离仅为2。也就是从虚拟头节点到当前节点的距离比到下一个节点的距离还短的时候，那说明肯定出现了环，并且当前节点即-4是环的"最右"节点，而下一个节点即2是环的入口。也即是 now，而如果节点的下一个节点是自身，那就是 now=last，所以判断条件就是 now<=last

class Solution {
   public:
    ListNode* detectCycle(ListNode* head) {
        ListNode* dummyHead = new ListNode(0,head);
        ListNode* cur = head;
        int now = 0,last = 0;   // now记录从虚拟头节点到当前结点的距离，last保存上一个now的值
        while(cur!=nullptr){
            ListNode* tmp = dummyHead;
            now = 0;
            while(tmp!=cur){
                tmp = tmp->next;
                now++;
            }
            // 核心语句：当last值小于等于now值说明cur是环的起点
            if(now <= last){
                return cur;
            }
            last = now; // last保存上一个now值
            cur = cur->next;
        }
        return nullptr;
    }
};

• 时间复杂度：O(n^2)。这段代码的核心是两个嵌套的 while 循环，外层循环遍历链表中的每个节点，内层循环遍历链表中从虚拟头节点到当前节点的距离。因此，总的时间复杂度为 O(n^2)。
• 空间复杂度：O(1)。这段代码只使用了常数级别的额外空间，即定义了几个指针和两个整型变量，因此空间复杂度为 O(1)。

但这种解法的时间复杂度为 O(n^2)，并非最优解，如果用哈希表来判断是否出现重复也只需要 O(n)。但由于只是想记录下自己的解法，所以也写出来了，算是拓展途径。由于代码随想录中的哈希表在后面章节，并且此题哈希表也不是最优解，因此这里就不放哈希表的解法了。

双指针

1.怎么确定是否有环？

使用两个指针 fast 和 slow，fast 指针每次走两步，slow 指针每次走一步。如果有环，那么它们一定会在环内某处相遇。

原因：如果有环，那么两个指针一定最后是在环内一直转圈，而由于 fast 指针每次都比慢指针多走一步。可以理解成快指针每次都和慢指针的距离缩小1步，那么他们之间的距离最终一定会缩减为0即相遇。

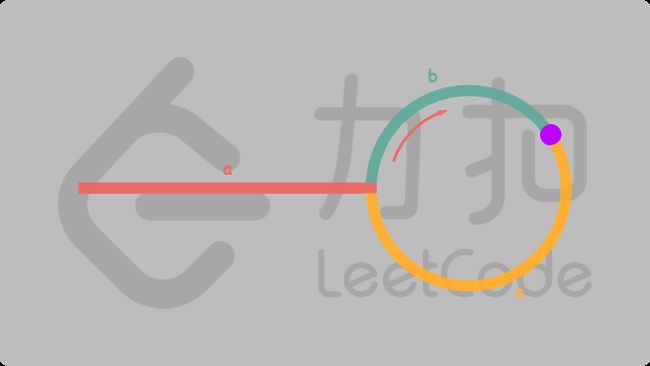
2.确定有环后怎么确定环的入口？

这里就要用到数学推导了。如下图，a 为头结点到环入口的距离，b 为环入口到相遇点(紫色)的距离，c 为相遇点到环入口的距离。那么 fast 指针走的距离 S_f = a+n(b+c)+b，而 slow 指针走的距离为 S_s=a+b，那么就有

S _f=2S _s即 a+n(b+c)+b = 2(a+b)即 a=c+(n-1)(b+c)

也就是从头节点到环入口的距离刚好等于 n-1圈的环加上 c 的距离，也就是说当快慢指针相遇时，我们可以再定义一个指针起始点为头节点，每次和 slow 指针一样也是走一步，那么根据上面的式子他们一定会在环的入口相遇。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        // 链表为空或者只有一个节点且无环时直接返回nullptr
        while(fast != nullptr && fast->next != nullptr) {
            // 慢指针走一步，快指针走两步
            slow = slow->next;
            fast = fast->next->next;
            // 快慢指针相遇，此时从head和相遇点，同时移动直至相遇
            if (slow == fast) {
                ListNode* ptr = head;
                while (ptr != slow) {
                    ptr = ptr->next;
                    slow = slow->next;
                }
                return ptr; // 返回环的入口
            }
        }
        return nullptr;
    }
};

• 时间复杂度：O(n)。其中 n 为链表中节点的数目。在最初判断快慢指针是否相遇时，slow 指针走过的距离不会超过链表的总长度；随后寻找入环点时，走过的距离也不会超过链表的总长度。因此，总的执行时间为 O(n)+O(n)=O(n)。
• 空间复杂度：O(1)。我们只使用了 slow，last 和 ptr 三个指针。

总结