Leetcode算法刷题笔记5-二叉树

相关刷题笔记博客
竞赛常用模板整理（ACM/ICPC/CCSP）
Leetcode算法刷题笔记1-链表
Leetcode算法刷题笔记2-栈、队、堆
Leetcode算法刷题笔记3-递归与回溯
Leetcode算法刷题笔记4-贪心
Leetcode算法刷题笔记5-二叉树
Leetcode算法刷题笔记6-图
Leetcode算法刷题笔记7-动态规划
Leetcode算法刷题笔记8-二分查找

Leetcode 113. 路径总和 II

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reverse-linked-list/

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

          5
         / \
        4   8
       /   / \
      11  13  4
     /  \    / \
    7    2  5   1

返回:

[ [5,4,11,2], [5,8,4,5] ]

#include

using namespace std;
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
//Leetcode提交部分 
class Solution {
public:
    vector<vector<int> > pathSum(TreeNode* root, int sum) {
        vector<vector<int> >result;
		vector<int> path;
		int value = 0;
		order(root,value,sum,path,result);
		return result; 
    }
private:
	void order(TreeNode *root,int &value,int sum,vector<int> &path,vector<vector<int> >&result){
		if(!root){
			return ;//如果节点不存在返回空 
		}
		value += root->val;//走到当前节点路径权值和 
		path.push_back(root->val);//压栈，存储路径权值到栈中 
		if(value==sum&&!root->left&&!root->right){//计算栈中数据总和有没有达到目标值 
			result.push_back(path);
		} 
		order(root->left,value,sum,path,result);//遍历左子树 
		order(root->right,value,sum,path,result);//遍历右子树 
		value -= root->val; //回溯时，减去总和中的数值 
		path.pop_back();    // 并且删除回溯的那个节点
	}
};
//Leetcode自行使用编译器（如DEV\VC\VS）测试部分 
int main(){
	TreeNode a(5);
	TreeNode b(4);
	TreeNode c(8);
	TreeNode d(11);
	TreeNode e(13);
	TreeNode f(4);
	TreeNode g(7);
	TreeNode h(2);
	TreeNode k(5);
	TreeNode l(1);
	a.left = &b;	a.right = &c;
	b.left = &d;	
	c.left = &e;	c.right = &f;
	d.left = &g;	d.right = &h;
	f.left = &k;	f.right = &l;
	Solution solve;
	vector<vector<int> > result = solve.pathSum(&a,22);
	for(int i=0;i<result.size();i++){
		cout<<"[";
		for(int j=0;j<result[i].size();j++){
		
			cout<<result[i][j]<<",";
		}
		cout<<"]"<<endl;
	}
	return 0;
}

Leetcode 236. 二叉树的最近公共祖先

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

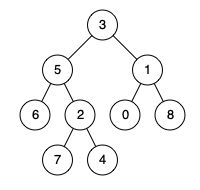
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

#include

using namespace std;
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
//Leetcode提交部分
void preorder(TreeNode* node,           //正在遍历的节点 
			  TreeNode* search,			//等待搜索的节点 
			  vector<TreeNode*> &path,	//遍历时的节点路径栈 
			  vector<TreeNode*> &result,//最终搜索到节点search的路径结果 
			  int &finish				//记录是否找到节点searh的变量，未找到是0，找到是1 
			  ){
	if(!node||finish){					//当node为空或者已经找到search节点直接返回并且结束 
		return;
	}
	path.push_back(node);				//先序遍历，将节点压入path栈 
	if(node == search){
		finish = 1;						//当找到search节点后，标记finish变量 
		result = path;					//将当前path存储到result 
	}
	preorder(node->left ,search,path,result,finish);  //深度遍历node左孩子 
	preorder(node->right,search,path,result,finish); //深度遍历node有孩子 
	path.pop_back();					//结束遍历node时，将node节点弹出path栈 
	}
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> path;						//声明遍历所用临时栈 
        vector<TreeNode*> node_p_path;				//存储p节点路径 
        vector<TreeNode*> node_q_path;				//存储q节点路径 
        int finish = 0;								//记录是否完成搜索的变量finish 
        preorder(root,p,path,node_p_path,finish);
        path.clear();
        finish = 0;									//清空path、finish、计算q节点路径 
        preorder(root,q,path,node_q_path,finish);
        int path_len = 0;							//路径长度 
        if(node_p_path.size()<node_q_path.size()){
        	path_len = node_p_path.size();
        }else{
        	path_len = node_q_path.size();
        }
        TreeNode *result = 0;						//同时遍历跟到p、q两个节点的路径上节点 
        for(int i=0;i<path_len;i++){
        	if(node_p_path[i] == node_q_path[i]){
        		result = node_p_path[i];			//找到最近公共祖先 
        	}
        }
        return result;
    }
}; 
//Leetcode自行使用编译器（如DEV\VC\VS）测试部分 
int main() {
    TreeNode a(3);
    TreeNode b(5);
    TreeNode c(1);
    TreeNode d(6);
    TreeNode e(2);
    TreeNode f(0);
    TreeNode x(8);
    TreeNode y(7);
    TreeNode z(4);
    a.left  = &b;
    a.right = &c;
    b.left  = &d;
    b.right = &e;
    c.left  = &f;
    c.right = &x;
	e.left  = &y;
	e.right = &z;
	Solution solve;
	TreeNode *result = solve.lowestCommonAncestor(&a,&b,&f);
	cout<<"lowestCommonAncestor = "<<result->val<<endl;
	
	result = solve.lowestCommonAncestor(&a,&b,&z);
	cout<<"lowestCommonAncestor = "<<result->val<<endl;
	
	result = solve.lowestCommonAncestor(&a,&b,&y);
	cout<<"lowestCommonAncestor = "<<result->val<<endl;
    return 0;
} 

尾语

诚邀各校各地有志之士加入我们大学生IT学习群交流：871352155（请各位广告大佬高抬贵手，常讨论学习无关的朋友请出门右拐∑(っ°Д°;)っ）