Python 学习 ---＞ Numpy可视化、快速入门、基础知识

​NumPy 官方文档 ( 快速开始，用户手册、参考 )：https://numpy.org/doc/stable/index.html

NumPy 中文文档

• ：https://www.numpy.org.cn/index.html
• ：https://numpy123.com/

NumPy 教程：http://www.runoob.com/numpy/numpy-tutorial.html
​​用 Python 做科学计算(PDF+源码)：https://download.csdn.net/download/freeking101/10959832
​用 Python 做科学计算：基础篇、手册篇、实战篇：http://old.sebug.net/paper/books/scipydoc/index.html

100 道 NumPy 练习题：https://github.com/rougier/numpy-100

NumPy：N维数组容器，以矩阵为主，纯数学。科学计算包
SciPy：科学计算函数库。比如：傅立叶变换。科学工具集
Pandas：表格容器。基于 NumPy。
Matplotlib: Python中最著名的绘图系统。画图工具包
Scipy：专为科学和工程设计的Python工具包
scikit-learn：机器学习相关的算法（如聚类算法，SVM等）。机器学习工具集

数学研究，对于 NumPy 和 pandas，建议选择 pandas

1、NumPy 简介

NumPy 是什么

NumPy是Python中用于科学计算的基本包。它是一个Python库，提供多维数组对象、各种派生对象(如掩码数组和矩阵)，以及一系列用于快速操作数组的例程，包括：数学、逻辑、形状操作、排序、选择、I/O、离散傅里叶变换、基本线性代数、基本统计操作、随机模拟 等等。

NumPy 包的核心是 ndarray 对象。这它封装了相同数据类型的n维数组，为了提高性能，许多操作都是在编译后的代码中执行。NumPy数组 和 标准Python序列 之间有几个重要的区别:

• NumPy 数组在创建时具有固定大小，与 Python 列表不同 （可以动态增长）。更改 ndarray 的大小将 创建新阵列并删除原始阵列。

• NumPy 数组中的元素都需要相同 数据类型，因此在内存中的大小将相同。例外情况： 可以有（Python，包括NumPy）对象的数组，从而 允许不同大小的元素数组。

• NumPy数组有助于高级数学和其他类型的 对大量数据进行操作。通常，此类操作是 执行效率更高，代码更少，比使用 Python 的内置序列。

• 越来越多的基于Python的科学和数学 包使用 NumPy 数组;虽然这些通常支持 python序列输入，它们在之前将此类输入转换为NumPy数组 进行处理，并且它们经常输出 NumPy 数组。换句话说， 为了有效地利用当今的大部分（甚至大部分） 基于Python的科学/数学软件，只知道如何 使用 Python 的内置序列类型是不够的 - 一个也 需要知道如何使用 NumPy 数组。

关于序列大小和速度的要点在 科学计算。

安装 Numpy

方法 1：pip install numpy

方法2：使用 Anaconda ( https://www.anaconda.com/products/distribution )  - 它包括 Python，NumPy和许多其他常用的科学计算包 和数据科学。

推荐使用 方法 2.

2、Numpy 可视化

图解 | NumPy可视化指南

：https://job.yanxishe.com/texttranslation/3198

：https://zhuanlan.zhihu.com/p/504917890

Numpy 可视化

Numpy和数据展示的可视化介绍：http://www.junphy.com/wordpress/index.php/2019/10/24/visual-numpy/

原文地址： https://jalammar.github.io/visual-numpy/

有兴趣的还可以来：Neo4j导入思知开源的1.4亿规模的中文知识图谱

NumPy 包是Python生态中数据分析，机器学习和科学计算领域的主力工具包。它极大地简化了对向量和矩阵地处理。一些主要的开发工具包也是基于 NumPy 作为基础工具包来开发的，比如 scikit-learn, SciPy, pandas, and tensorflow 。除了对数值数据进行切片和交叉分析，掌握Numpy为在你处理和调试这些库的时候给你带来优势。

在这篇文章中，在我们应用到机器学习模型之前，我们会看到 NumPy 的主要使用方式以及它如何展示不同类型的数据（表格，图像，文本等）

import numpy as np

data = np.array([1, 2, 3])
print(data)

创建数组

我们可以通过传递一个 python 列表，使用方法 “np.array()” 创建一个 NumPy 数组。如下图，python创建了一个如右图所示的数组：

在很多场景下，我们希望 NumPy 能够帮我们初始化数组。 NumPy 提供了一些方法，比如 ones(), zeros() 和 random.random()。 我们只需要提供数组大小，如图：

一旦创建好数组后，就可以自由地操纵他们了。

数组运算

我们首先创建两个 NumPy 数组，一个是 data 数组，一个是 ones数组：

将他们按照位置顺序（比如每行的值）相加，data + ones:

当我学这些的时候我意识到这可以让我不需要在代码中使用循环来计算这些。这种抽象能让你站在更高的角度去考虑问题。并且，不只有加法，我们还可以以如下方式去计算：

有一些经常需要计算一个数组和一个数字的操作（也称作对向量和标量的操作）。比如，我们的数组用英里表示距离，我们想转换成公里（ 1英里(mi) = 1.60934千米(公里) ），可以使用：data * 1.6: 

可以看到 NumPy 的乘法机制是对每一个单元都进行计算，这是称作 广播（broadcast）的一种机制，是非常有用的。

索引

我们可以对 NumPy 数组进行索引或者切片就像对 python 列表一样的操作：

聚合

NumPy 提供的另外一个优点是聚合功能：

除了 min, max 和 sum, 还有 mean 可以获取平均值，prod 可以获取所有元素相乘的结果， std 可以获取标准差，等等其他功能

多维

目前我们看到的例子都是一维向量。 NumPy 一个优雅的特性就是能将我们目前看到的所有特性扩展到任何维度。

创建矩阵

我们可以传递一个 python 列表（多维列表），如下图，使用 NumPy 去创建一个矩阵来表示他们：np.array([[1,2],[3,4]])

还可以使用上面提到的方法（ ones(), zeros(), 和 random.random() ）只要提供一个元组来描述矩阵的维度信息，如下图：

矩阵运算

如果两个矩阵的行列数相同，我们可以使用运算符（+ - * /）对矩阵进行运算。NumPy 也是基于位置来进行操作：

这些运算符也可以在不同的行列数的矩阵上使用只要不同维度的矩阵是一个一维矩阵（例如，只有一行或一列），在这种形式上， NumPy 使用了 broadcast 规则来进行计算：

点积（Dot Product）

和前面的算术运算的一个关键区别是在对矩阵进行这类乘法（传统意义的矩阵相乘（译者注））时使用点积操作时，NumPy 为矩阵提供了一个 dot() 方法，可以计算出矩阵的点积： 

我已经在图片的底部加入了矩阵的维度信息，强调了不同维度的矩阵，在点乘时相邻的维度必须相同（就是 1×3 的矩阵和 3×2的矩阵相乘，前者的列维度和后者的行维度相同（译者注））。你可以想象是进行了如下的操作： 

矩阵索引

当我们使用矩阵的时候索引和切片功能将更加有用：

矩阵聚合 

与向量（数组）相同，可以对矩阵进行类似的聚合操作：

而且不仅可以对矩阵中的所有值进行聚合，还能对行或列进行单独的聚合操作，使用 axis 参数进行指定（axis是轴的意思）：

置换和变形

当处理矩阵时一个共用功能就是矩阵的变换。比如当需要计算两个矩阵的点积的时候可能需要对齐矩阵相邻的维度（使矩阵能够进行点积运算）。NumPy 的数组有一个很方便的属性 T 可以获取矩阵的转置：

在更高级的场合，你可能发现需要变换矩阵的维度。这在机器学习中时经常常见的，比如当一个特定的模型需要一个一个特定维度的矩阵，而你的数据集的输入数据维度不一样的时候。NumPy 的 reshape() 函数就变得有用了。你只需指定你需要的新的矩阵的维度即可。你还可以通过将维度指定为 -1，NumPy 可以依据矩阵推断出正确的维度：

更高维度

在更高的维度，前面提及的，NumPy 都可以做到。其中一个主要原因就是被称为 ndarray(N-Dimensional Array)的数据结构。

在大部分场合，处理一个新的维度只需要在 NumPy 的函数上参数上增加一个维度： 

注意：需要记住的是，当你打印一个3维的 NumPy 数组时，文本的输出和这里展示的不一样。NumPy 对多维数组的打印顺序是最后一个轴是最快打印的，而第一个是最后的。比如， np.ones((4, 3, 2)) 将会打印如下： 

array([[[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]]])

实际使用

现在是获取成果的时候了，下面是一些 NumPy 将会帮助你的一些例子。

公式

实现在矩阵和向量上的数学公式是NumPy的一个关键用处，这也是为什么 NumPy 是python 科学计算领域的宠儿。例如， 均方误差公式是解决回归问题的有监督机器学习模型的一个关键。

用 NumPy 来实现是一件轻而易举的事：

优雅之处在于 numpy 不关心 predictions 和 labels 的容量是 1 还是几百个值（只要它们有同样的容量）。我们可以通过如下四个步骤来对这行代码进行一个序列走读：

predictions 和 labels 向量都有3个值，也就是说 n = 3, 计算完减法后，我们得到如下的公式： 

然后对这个向量求平方操作： 

 

现在，我们对三个数进行求和：

error 中的值就是模型预测的质量

数据展示

考虑到所有可能需要处理和构建模型的数据类型（电子表格，图像，音频等）。很多是很适合用一个n维数组进行表示的。

电子表格

• 电子表格是一个二维矩阵，每一个 sheet 页都有它的变量。python 中最流行的一个框架是 pandas dataframe ，这也是一个使用 NumPy 构建的一个软件包。 

音频和时间序列数据

• 一个音频文件是一个以为数组的样本。 每个样本都是一个数字，代表一小块音频信号。 cd质量的音频每秒可能有44,100个样本，每个样本是-32767到32768之间的整数。 这意味着如果您有一个10秒的cd质量的WAVE文件，您可以将它装入一个长度为10 * 44,100 = 441,000的NumPy数组中。 如果想提取音频的第一秒，只需将该文件加载到一个NumPy数组 audio 中，并使用 audio[:44100]即可获取到。

下面是一个音频文件的一个切片：

时间序列的数据也是一样（比如， 随时间变化的股票价格 ）

图像

• 一个图像就是一个像素矩阵，其维度就是高度 x 宽度。
  • 如果图像是黑白照片，也就是一个灰度图，每个像素可以用一个数字代表（通常是在0（黑）和255（白）之间）。如果 想要裁切图像左上角10 x 10像素的部分，只需通过 NumPy 的 image[:10, :10] 函数即可获取

下面是一个图片文件的切片：

• 如果是一个彩色图像，那么每个像素可以用3个数字表示——一个代表红色，一个代表绿色，一个代表蓝色。这种情况下，我们需要一个3维素组（因为每个单元仅可以包含一个数字）。因此，一个彩色图像可以被一个 ndarray 维度表示：（高度 * 宽度 * 3）：

语言

如果我们处理的是文本的话，情况可能有点不同。要用数值表示一段文本需要构建一个词汇表（模型需要知道的所有的唯一词）以及一个词嵌入（embedding）过程。 让我们看看用数字表示这个谚语的步骤：” Have the bards who preceded me left any theme unsung?”

模型需要先训练大量文本才能用数字表示这位诗人的诗句。我们可以让模型处理一个小数据集，并使用这个数据集来构建一个词汇表（71,290个单词）：

这个句子可以被划分为一系列词（token）（基于通用规则）：

然后我们用词汇表中单词的ID来替换它：

对于模型来说，这些ID并没有提供更多的信息。因此，在将这些词喂入模型之前，需要先将她们替换为对应的词嵌入向量（本例中使用50维度的 word2vec 词嵌入）

可以看出这个 NumPy 数组有 [词嵌入维度 * 序列长度] 的维数。在实践中可能有另外的情况，在此我用这种方式来表示。出于性能因素的考虑，深度学习模型倾向于保存批处理数据的第一个维度（因为如果并行地训练多个实例，模型可以训练得更快）。reshape() 在这里就发挥了用武之地。比如像 BERT 这样的模型，他的输入希望是这种[批处理大小, 序列长度, 词嵌入维度]([ batch_size, sequence_length, embedding_size ]) 形状的。

现在，这些就是一个模型可以处理并且使用的一个数值型卷积向量。我在上图中的其他行留了空白，但是他们实际是被填充用于训练（或者是预测）。

3、快速入门

官网文档 - 快速入门

• 英文版：https://numpy.org/doc/stable/user/quickstart.html
• 中文版：https://www.numpy.org.cn/user/quickstart.html

先决条件

电脑上安装了以下一些软件:

• Python
• NumPy

这些是可能对你有帮助的:

• ipython是一个净强化的交互Python Shell，对探索NumPy的特性非常方便。
• matplotlib将允许你绘图
• Scipy在NumPy的基础上提供了很多科学模块

基础篇

NumPy的主要对象是同种元素的多维数组。这是一个所有的元素都是一种类型、通过一个正整数元组索引的元素表格(通常是元素是数字)。在NumPy中维度(dimensions)叫做轴(axes)，轴的个数叫做秩(rank)。

例如，在3D空间一个点的坐标[1, 2, 3]是一个秩为1的数组，因为它只有一个轴。那个轴长度为3.又例如，在以下例子中，数组的秩为2(它有两个维度).第一个维度长度为2,第二个维度长度为3.

[[ 1., 0., 0.],
 [ 0., 1., 2.]]

NumPy的数组类被称作ndarray。通常被称作数组。注意numpy.array和标准Python库类array.array并不相同，后者只处理一维数组和提供少量功能。更多重要ndarray对象属性有：

• ndarray.ndim    数组轴的个数，在python的世界中，轴的个数被称作秩
• ndarray.shape    数组的维度。这是一个指示数组在每个维度上大小的整数元组。例如一个n排m列的矩阵，它的shape属性将是(2,3),这个元组的长度显然是秩，即维度或者ndim属性
• ndarray.size    数组元素的总个数，等于shape属性中元组元素的乘积。
• ndarray.dtype    一个用来描述数组中元素类型的对象，可以通过创造或指定dtype使用标准Python类型。另外NumPy提供它自己的数据类型。
• ndarray.itemsize    数组中每个元素的字节大小。例如，一个元素类型为float64的数组itemsiz属性值为8(=64/8),又如，一个元素类型为complex32的数组item属性为4(=32/8).
• ndarray.data    包含实际数组元素的缓冲区，通常我们不需要使用这个属性，因为我们总是通过索引来使用数组中的元素。

查看 np 的所有属性

import numpy as np

list(map(lambda x=None: print(f"{x} ---> {getattr(np, x)}"), dir(np)))

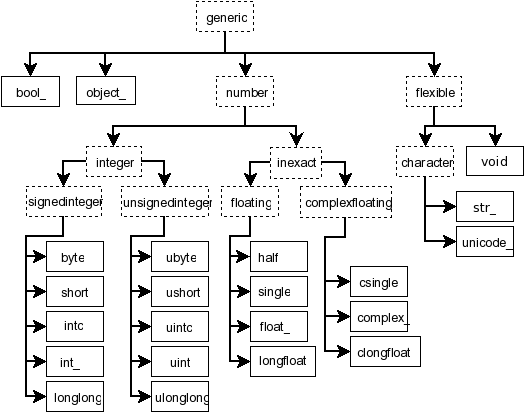
dtype：https://numpy.org/doc/stable/reference/arrays.html

NumPy 24种数据类型：https://numpy.org/doc/stable/reference/arrays.scalars.html

数组数据类型的类型对象层次结构。未显示的是两个整数类型 intp 和 uintp，它们只是指向持有平台指针的整数类型。所有的数字类型也可以使用位宽名称来获得。

一个例子

>>> from numpy  import *
>>> a = arange(15).reshape(3, 5)
>>> a
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])
>>> a.shape
(3, 5)
>>> a.ndim
2
>>> a.dtype.name
'int32'
>>> a.itemsize
4
>>> a.size
15
>>> type(a)
numpy.ndarray
>>> b = array([6, 7, 8])
>>> b
array([6, 7, 8])
>>> type(b)
numpy.ndarray

创建 数组

有几种方法可以创建数组。

使用 array() 函数从常规的 Python列表和元组创造数组。所创建的数组类型由原序列中的元素类型推导而来。

>>> from numpy  import *
>>> a = array( [2,3,4] )
>>> a
array([2, 3, 4])
>>> a.dtype
dtype('int32')
>>> b = array([1.2, 3.5, 5.1])
>>> b.dtype
dtype('float64')  一个常见的错误包括用多个数值参数调用`array`而不是提供一个由数值组成的列表作为一个参数。
 
>>> a = array(1,2,3,4)    # WRONG
>>> a = array([1,2,3,4])  # RIGHT

数组将序列包含序列转化成二维的数组，序列包含序列包含序列转化成三维数组等等。

>>> b = array( [ (1.5,2,3), (4,5,6) ] )
>>> b
array([[ 1.5,  2. ,  3. ],
       [ 4. ,  5. ,  6. ]])

数组类型可以在创建时显示指定

>>> c = array( [ [1,2], [3,4] ], dtype=complex )
>>> c
array([[ 1.+0.j,  2.+0.j],
       [ 3.+0.j,  4.+0.j]])

通常，数组的元素开始都是未知的，但是它的大小已知。因此，NumPy提供了一些使用占位符创建数组的函数。这最小化了扩展数组的需要和高昂的运算代价。

函数function创建一个全是0的数组，函数ones创建一个全1的数组，函数empty创建一个内容随机并且依赖与内存状态的数组。默认创建的数组类型(dtype)都是float64。

>>> zeros( (3,4) )
array([[0.,  0.,  0.,  0.],
       [0.,  0.,  0.,  0.],
       [0.,  0.,  0.,  0.]])
>>> ones( (2,3,4), dtype=int16 )                # dtype can also be specified
array([[[ 1, 1, 1, 1],
        [ 1, 1, 1, 1],
        [ 1, 1, 1, 1]],
       [[ 1, 1, 1, 1],
        [ 1, 1, 1, 1],
        [ 1, 1, 1, 1]]], dtype=int16)
>>> empty( (2,3) )
array([[  3.73603959e-262,   6.02658058e-154,   6.55490914e-260],
       [  5.30498948e-313,   3.14673309e-307,   1.00000000e+000]])

为了创建一个数列，NumPy 提供一个类似 arange 的函数返回数组而不是列表:

>>> arange( 10, 30, 5 )
array([10, 15, 20, 25])
>>> arange( 0, 2, 0.3 )                 # it accepts float arguments
array([ 0. ,  0.3,  0.6,  0.9,  1.2,  1.5,  1.8])

当arange使用浮点数参数时，由于有限的浮点数精度，通常无法预测获得的元素个数。因此，最好使用函数linspace去接收我们想要的元素个数来代替用range来指定步长。

>>> from numpy import pi
>>> np.linspace(0, 2, 9)                   # 9 numbers from 0 to 2
array([0.  , 0.25, 0.5 , 0.75, 1.  , 1.25, 1.5 , 1.75, 2.  ])
>>> x = np.linspace(0, 2 * pi, 100)        # useful to evaluate function at lots of points
>>> f = np.sin(x)

其它函数：array, zeros, zeros_like, ones, ones_like, empty, empty_like, arange, linspace, numpy.random.Generator.rand, numpy.random.Generator.randn, fromfunction, fromfile

示例：

import numpy as np

arr0 = np.array((1, 2, 3, 4, 5))  # 括号内为元组
arr1 = np.array([1, 2, 3, 4])  # 括号内为列表
arr2 = np.array([[1, 2, 3, 4], [4, 5, 6, 7], [8, 9, 10, 11]])
arr4 = np.array(range(10))  # 迭代对象
arr5 = np.array([i ** 2 for i in range(5)])  # 迭代对象
print(f"创建的一维ndarray为：{arr0}")
print(f"创建的一维ndarray为：{arr1}")
print(f"创建的二维ndarray为：\n{arr2}")
print(f"创建的一维ndarray为：{arr4}")
print(f"创建的一维ndarray为：{arr5}")

import numpy as np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array([[1, 2, 3, 4], [4, 5, 6, 7], [8, 9, 10, 11]])
print(f"arr1的轴的个数：{arr1.ndim}")
print(f"arr2的轴的个数：{arr2.ndim}")
print(f"arr1的维度：{arr1.shape}")
print(f"arr2的维度：{arr2.shape}")
print(f"arr1的元素个数：{arr1.size}")
print(f"arr2的元素个数：{arr2.size}")
print(f"arr1的数据类型：{arr1.dtype}")
print(f"arr2的数据类型：{arr2.dtype}")
print(f"arr1的每个元素字节大小：{arr1.itemsize}")
print(f"arr2的每个元素字节大小：{arr2.itemsize}")

import numpy as np
print(f"使用arange函数创建ndarray1为：\n{np.arange(0, 10, 2)}")
print(f"使用arange函数创建ndarray2为：\n{np.arange(10, 1)}")
print(f"使用arange函数创建ndarray3为：\n{np.arange(10, step = 1)}")

import numpy as np
print(f"使用arange函数创建ndarray为：\n{np.arange(0, 1, 0.1)}")
print(f"使用linspace函数创建ndarray为：\n{np.linspace(0, 1, 5)}")
# 下面创建是从1（10的0次方）到100（10的二次方），这10个元素的等比数列
print(f"使用logspace函数创建ndarray为：\n{np.logspace(0, 2, 10)}")
print(f"使用zeros函数创建ndarray为：\n{np.zeros((2, 3))}")
print(f"使用eye函数创建ndarray为：\n{np.eye(3)}")
print(f"使用diag函数创建ndarray为：\n{np.diag([2, 3, 4])}")
print(f"使用ones函数创建ndarray为：\n{np.diag((3, 2))}")

import numpy as np
print(f"使用random函数生成的随机数ndarray为：\n{np.random.random(5)}")
print(f"使用rand函数生成服从均匀分布的随机数ndarray为：\n{np.random.rand(3, 5)}")
print(f"使用randint函数生成给定上下限的随机整数ndarray为：\n{np.random.randint(2, 10,[2, 3])}")

 ndarray 的索引与切片

一维 ndarray的索引

import numpy as np
# 默认 np.arange(0, 10, 1)
arr = np.arange(10)
print(f"初始结果为：{arr}")
print(f"使用元素位置索引结果为：{arr[5]}")
print(f"使用元素位置切片结果为：{arr[2:5]}")
print(f"使用元素位置切片结果为：{arr[2:8:2]}")
print(f"省略单个位置切片结果为：{arr[:5]}")
print(f"使用元素反向位置切片结果为：{arr[:-2]}")
# 修改对应下标的值
arr[2:5] = 10, 11, 13
print(f"修改后结果为：{arr}")

 多维 ndarray的索引，多维 ndarray的每个维度都有一个索引，各个维度的索引之间用逗号隔开。

import numpy as np
 
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(f"初始结果为：\n{arr}")
# 取第二列
print(f"切片结果为：\n{arr[:, 1:2]}")
# 取1、2两行，2、3两列
print(f"切片结果为：\n{arr[0:2, 1:3]}")
# 取 arr中（0，1）、（0，2）、（2，0）的值
print(f"索引结果为：\n{arr[[0, 0, 2], [1, 2,0]]}")
# bool索引
print(f"索引结果为：\n{arr>6}")
print(f"索引结果为：\n{arr[arr>6]}")

import numpy as np

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(f"初始结果为：\n{arr}")
print(f"arr[...,1]切片结果为：\n{arr[..., 1]}")
print(f"arr[...,1:]切片结果为：\n{arr[..., 1:]}")
print(f"arr[:,1:]切片结果为：\n{arr[:, 1:]}")

Numpy基础入门知识点总结：https://blog.csdn.net/Xx_Studying/article/details/127365627

打印数组

当你打印一个数组，NumPy以类似嵌套列表的形式显示它，但是呈以下布局：

• 最后一个轴从左到右打印，
• 倒数第二个从上到下打印，
• 其余的也从上到下打印，每个切片通过一个空行与下一个隔开

一维数组被打印成行，二维数组成矩阵，三维数组成矩阵列表。

>>> a = arange(6)                         # 1d array
>>> print a
[0 1 2 3 4 5]
>>>
>>> b = arange(12).reshape(4,3)           # 2d array
>>> print b
[[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]
>>>
>>> c = arange(24).reshape(2,3,4)         # 3d array
>>> print c
[[[ 0  1  2  3]
  [ 4  5  6  7]
  [ 8  9 10 11]]
 
 [[12 13 14 15]
  [16 17 18 19]
  [20 21 22 23]]]

查看形状操作一节获得有关reshape的更多细节

如果一个数组用来打印太大了，NumPy自动省略中间部分而只打印角落

>>> print arange(10000)
[   0    1    2 ..., 9997 9998 9999]
>>>
>>> print arange(10000).reshape(100,100)
[[   0    1    2 ...,   97   98   99]
 [ 100  101  102 ...,  197  198  199]
 [ 200  201  202 ...,  297  298  299]
 ...,
 [9700 9701 9702 ..., 9797 9798 9799]
 [9800 9801 9802 ..., 9897 9898 9899]
 [9900 9901 9902 ..., 9997 9998 9999]]

禁用NumPy的这种行为并强制打印整个数组，你可以设置printoptions参数来更改打印选项。

>>> set_printoptions(threshold='nan')

基本运算

数组的算术运算是按元素的。新的数组被创建并且被结果填充。

不像许多矩阵语言，NumPy中的乘法运算符*指示按元素计算，矩阵乘法可以使用dot函数或创建矩阵对象实现(参见教程中的矩阵章节)

有些操作符像+=和*=被用来更改已存在数组而不创建一个新的数组。

当运算的是不同类型的数组时，结果数组和更普遍和精确的已知(这种行为叫做upcast)。

许多非数组运算，例如计算数组中所有元素的和，都是作为ndarray类的方法实现的。

默认情况下，这些操作应用于数组，就像它是一个数字列表一样，而不管其形状如何。但是，通过指定axis参数，你可以沿着数组的指定轴应用一个操作:

通用功能

NumPy提供常见的数学函数如sin,cos和exp。在NumPy中，这些叫作“通用函数”(ufunc)。在NumPy里这些函数作用按数组的元素运算，产生一个数组作为输出。

参看：all, any, apply_along_axis, argmax, argmin, argsort, average, bincount, ceil, clip, conj, corrcoef, cov, cross, cumprod, cumsum, diff, dot, floor, inner, invert, lexsort, max, maximum, mean, median, min, minimum, nonzero, outer, prod, re, round, sort, std, sum, trace, transpose, var, vdot, vectorize, where

索引、切片和迭代

一维数组可以被索引、切片和迭代，就像列表和其它Python序列。

多维数组可以每个轴有一个索引。这些索引由一个逗号分割的元组给出。

当少于轴数的索引被提供时，确失的索引被认为是整个切片：

b[i]中括号内的表达式被视为i，后面跟着尽可能多的:实例，以表示剩余的轴。NumPy还允许您使用点作为b[i，…]。

点(…)表示生成一个完整的索引元组所需的冒号。例如，如果x是一个有5个轴的数组，那么

• x[1,2,…] 等同于 x[1,2,:,:,:],
• x[…,3] 等同于 x[:,:,:,:,3]
• x[4,…,5,:] 等同 x[4,:,:,5,:].

在多维数组上的迭代是根据第一个轴完成的:

但是，如果想对数组中的每个元素执行操作，可以使用flat属性，它是数组中所有元素的迭代器:

参看：Indexing on ndarrays, Indexing routines (reference), newaxis, ndenumerate, indices

形状操纵

更改数组的形状

一个数组的形状由它每个轴上的元素个数给出：

数组的形状可以用各种命令改变。注意，以下三个命令都返回一个修改后的数组，但不改变原始数组:

由ravel()展平的数组元素的顺序通常是“C风格”的，就是说，最右边的索引变化得最快，所以元素a[0,0]之后是a[0,1]。如果数组被改变形状(reshape)成其它形状，数组仍然是“C风格”的。NumPy通常创建一个以这个顺序保存数据的数组，所以ravel()将总是不需要复制它的参数3。但是如果数组是通过切片其它数组或有不同寻常的选项时，它可能需要被复制。函数reshape()和ravel()还可以被同过一些可选参数构建成FORTRAN风格的数组，即最左边的索引变化最快。

reshape函数改变参数形状并返回它，而resize函数改变数组自身。

如果一个维度在重塑操作中被指定为-1，其他维度将自动计算:

参看：ndarray.shape, reshape, resize, ravel

组合(stack)不同的数组

几个数组可以沿着不同的轴堆叠在一起:

函数 column_stack 将一维数组作为列堆叠到2D数组中。它只对2D数组等效于hstack:

 另一方面，对于任何输入数组，函数row_stack等价于vstack。实际上，row_stack是vstack的别名:

 一般来说，对于二维以上的数组，hstack将沿着它们的第二个轴堆栈，vstack将沿着它们的第一个轴堆栈，concatenate允许一个可选参数，给出应该发生连接的轴的编号。

注意：在复杂情况下，r_[]和c_[]对创建沿着一个方向组合的数很有用，它们允许范围符号(“:”):

当使用数组作为参数时，r_和c_的默认行为和vstack和hstack很像，但是允许一个可选参数，给出要连接的轴的编号。

参看：hstack, vstack, column_stack, concatenate, c_, r_

将一个数组分割(split)成几个小数组

使用hsplit你能将数组沿着它的水平轴分割，或者指定返回相同形状数组的个数，或者指定在哪些列后发生分割:

vsplit沿着纵向的轴分割，array split允许指定沿哪个轴分割。

复制和视图

当运算和处理数组时，它们的数据有时被拷贝到新的数组有时不是。这通常是新手的困惑之源。这有三种情况:

完全不拷贝

简单的赋值不拷贝数组对象或它们的数据。

Python将可变对象作为引用传递，因此函数调用不会复制。

视图(view)和浅复制

不同的数组对象分享同一个数据。视图方法创造一个新的数组对象指向同一数据。

切片数组返回它的一个视图：

深复制

这个复制方法完全复制数组和它的数据。

有时，如果不再需要原始数组，则应该在切片后调用copy。例如，假设a是一个巨大的中间结果，而最终结果b只包含了a的一小部分，那么在用切片构造b时应该做一个深度复制:

如果使用b = a[:100]，则a会被b引用，即使执行了del a, a也会持久化在内存中。

函数和方法(method)总览

下面是一些有用的NumPy函数和方法的列表，按类别排序。完整列表请参见例程。

创建 数组

arange, array, copy, empty, empty_like, eye, fromfile, fromfunction, identity, linspace, logspace, mgrid, ogrid, ones, ones_like, r_, zeros, zeros_like

转换

ndarray.astype, atleast_1d, atleast_2d, atleast_3d, mat

操作

array_split, column_stack, concatenate, diagonal, dsplit, dstack, hsplit, hstack, ndarray.item, newaxis, ravel, repeat, reshape, resize, squeeze, swapaxes, take, transpose, vsplit, vstack

查询

all, any, nonzero, where

排序

argmax, argmin, argsort, max, min, ptp, searchsorted, sort

运算

choose, compress, cumprod, cumsum, inner, ndarray.fill, imag, prod, put, putmask, real, sum

统计

cov, mean, std, var

基本线性代数

cross, dot, outer, linalg.svd, vdot

进阶

广播法则(rule)

广播允许通用函数以一种有意义的方式处理不完全相同形状的输入。

• 广播的第一个规则是，如果所有输入数组的维数不相同，则将在较小数组的形状前重复加上“1”，直到所有数组的维数相同。
• 广播的第二条规则确保在特定维度上大小为1的数组的行为就像它们具有该维度上形状最大的数组的大小一样。假定数组元素的值在“broadcast”数组的维度上是相同的。
• 应用广播规则后，所有数组的大小必须匹配。更多详情请参阅 广播。

用索引数组进行索引

NumPy提供了比常规Python序列更多的索引功能。除了按整数和切片进行索引外，如前所述，数组还可以按整数数组和布尔数组进行索引。

通过数组索引

当索引数组a是多维数组时，单个索引数组引用a的第一个维度。下面的示例通过使用调色板将标签图像转换为彩色图像来展示这种行为。

我们也可以给出一个以上维度的索引。每个维度的索引数组必须具有相同的形状。

在Python中，arr[i, j] 与 arr[(i, j)] 完全相同，因此我们可以将i和j放在一个元组中，然后对其进行索引。

然而，我们不能把i和j放在一个数组中，因为这个数组将被解释成索引 a 的第一维。

数组索引的另一个常见用途是搜索与时间相关的序列的最大值:

 你也可以使用索引数组作为目标来赋值:

然而，当索引列表包含重复时，赋值操作将执行多次，留下最后一个值:

这很合理，但如果你想使用Python的+=构造，就要小心了，因为它可能不会达到你的预期:

尽管0在索引列表中出现了两次，但第0个元素只加了一次。这是因为Python要求a += 1等价于a = a + 1。

通过布尔数组索引

当我们用(整数)索引数组索引时，我们提供了要选择的索引列表。对于布尔索引，方法是不同的;我们显式地选择数组中的哪些项是我们需要的，哪些是我们不需要的。

对于布尔索引，最自然的方法是使用与原始数组具有相同形状的布尔数组:

这个属性在赋值中非常有用:

你可以看看下面的例子，看看如何使用布尔索引来生成 Mandelbrot set(https://en.wikipedia.org/wiki/Mandelbrot_set) 的图像:

用布尔值进行索引的第二种方式更类似于整数索引;对于数组的每个维度，我们给出一个1D布尔数组，选择我们想要的切片:

注意，1D布尔数组的长度必须与要切片的维度(或轴)的长度一致。在前面的例子中，b1的长度为3 (a中的行数)，而b2(长度为4)适用于索引a的第二个轴(列)。

ix_() 函数

ix_函数可用于组合不同的向量，以获得每个n-uplet的结果。例如，如果你想计算从向量a, b和c中取的所有三联体的所有a+b*c:

你也可以像下面这样实现reduce:

然后把它用作:

与普通的 ufunc 相比，这个版本的reduce的优点。Reduce使用了 广播规则 ，以避免创建输出大小乘以向量数量的参数数组。

用字符串索引

参看：Structured arrays.

技巧和提示

下面我们给出简短和有用的提示。

“自动”改变形状

要改变一个数组的尺寸，你可以省略一个大小，然后自动推导:

向量组合(stacking)

我们如何从一列大小相等的行向量中构造一个二维数组?在MATLAB中这很简单:如果x和y是两个相同长度的向量，你只需要做m=[x;y]。在NumPy中，这是通过函数column_stack, dstack, hstack和vstack来工作的，这取决于要进行堆叠的维度。例如:

在二维以上的情况下，这些函数背后的逻辑可能很奇怪。

参看：NumPy for MATLAB users

柱状图

应用于数组的NumPy直方图函数返回一对向量:数组的直方图和bin边的向量。注意:matplotlib还有一个构建直方图的函数(在Matlab中称为hist)，它与NumPy中的函数不同。主要的区别是pylab。Hist自动绘制直方图，而numpy。直方图只生成数据。

使用 Matplotlib >=3.4 ，也可以使用 plt. stairs(n, bins).

线性代数

继续前进，基本线性代数包含在这里。

简单数组运算

参考numpy文件夹中的linalg.py获得更多信息

>>> from numpy import *
>>> from numpy.linalg import *
>>> a = array([[1.0, 2.0], [3.0, 4.0]])
>>> print a
[[ 1.  2.]
 [ 3.  4.]]
 
>>> a.transpose()
array([[ 1.,  3.],
       [ 2.,  4.]])
 
>>> inv(a)
array([[-2. ,  1. ],
       [ 1.5, -0.5]])
 
>>> u = eye(2) # unit 2x2 matrix; "eye" represents "I"
>>> u
array([[ 1.,  0.],
       [ 0.,  1.]])
>>> j = array([[0.0, -1.0], [1.0, 0.0]])
>>> dot (j, j) # matrix product
array([[-1.,  0.],
       [ 0., -1.]])
 
>>> trace(u)  # trace
 2.0
 
>>> y = array([[5.], [7.]])
>>> solve(a, y)
array([[-3.],
       [ 4.]])
 
>>> eig(j)
(array([ 0.+1.j,  0.-1.j]),
array([[ 0.70710678+0.j,  0.70710678+0.j],
       [ 0.00000000-0.70710678j,  0.00000000+0.70710678j]]))
Parameters:
    square matrix
 
Returns
    The eigenvalues, each repeated according to its multiplicity.
 
    The normalized (unit "length") eigenvectors, such that the
    column ``v[:,i]`` is the eigenvector corresponding to the
    eigenvalue ``w[i]`` .

矩阵类

这是一个关于矩阵类的简短介绍。

>>> A = matrix('1.0 2.0; 3.0 4.0')
>>> A
[[ 1.  2.]
 [ 3.  4.]]
>>> type(A)  # file where class is defined

 
>>> A.T  # transpose
[[ 1.  3.]
 [ 2.  4.]]
 
>>> X = matrix('5.0 7.0')
>>> Y = X.T
>>> Y
[[5.]
 [7.]]
 
>>> print A*Y  # matrix multiplication
[[19.]
 [43.]]
 
>>> print A.I  # inverse
[[-2.   1. ]
 [ 1.5 -0.5]]
 
>>> solve(A, Y)  # solving linear equation
matrix([[-3.],
        [ 4.]])

索引：比较矩阵和二维数组

注意NumPy中数组和矩阵有些重要的区别。NumPy提供了两个基本的对象：一个N维数组对象和一个通用函数对象。其它对象都是建构在它们之上 的。特别的，矩阵是继承自NumPy数组对象的二维数组对象。对数组和矩阵，索引都必须包含合适的一个或多个这些组合：整数标量、省略号 (ellipses)、整数列表;布尔值，整数或布尔值构成的元组，和一个一维整数或布尔值数组。矩阵可以被用作矩阵的索引，但是通常需要数组、列表或者 其它形式来完成这个任务。

像平常在Python中一样，索引是从0开始的。传统上我们用矩形的行和列表示一个二维数组或矩阵，其中沿着0轴的方向被穿过的称作行，沿着1轴的方向被穿过的是列。9

让我们创建数组和矩阵用来切片：

>>> A = arange(12)
>>> A
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])
>>> A.shape = (3,4)
>>> M = mat(A.copy())
>>> print type(A),"  ",type(M)
   
>>> print A
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
>>> print M
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]

现在，让我们简单的切几片。基本的切片使用切片对象或整数。例如，A[:]和M[:]的求值将表现得和Python索引很相似。然而要注意很重要的一点就是NumPy切片数组不创建数据的副本;切片提供统一数据的视图。

>>> print A[:]; print A[:].shape
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
(3, 4)
>>> print M[:]; print M[:].shape
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
(3, 4)

现在有些和Python索引不同的了：你可以同时使用逗号分割索引来沿着多个轴索引。

>>> print A[:,1]; print A[:,1].shape
[1 5 9]
(3,)
>>> print M[:,1]; print M[:,1].shape
[[1]
 [5]
 [9]]
(3, 1)

注意最后两个结果的不同。对二维数组使用一个冒号产生一个一维数组，然而矩阵产生了一个二维矩阵。10例如，一个M[2,:]切片产生了一个形状为(1,4)的矩阵，相比之下，一个数组的切片总是产生一个最低可能维度11的数组。例如，如果C是一个三维数组，C[...,1]产生一个二维的数组而C[1,:,1]产生一个一维数组。从这时开始，如果相应的矩阵切片结果是相同的话，我们将只展示数组切片的结果。

假如我们想要一个数组的第一列和第三列，一种方法是使用列表切片：

>>> A[:,[1,3]]
array([[ 1,  3],
       [ 5,  7],
       [ 9, 11]])

稍微复杂点的方法是使用take()方法(method):

>>> A[:,].take([1,3],axis=1)
array([[ 1, 3],
[ 5, 7],
[ 9, 11]])

如果我们想跳过第一行，我们可以这样：

>>> A[1:,].take([1,3],axis=1)
array([[ 5, 7],
[ 9, 11]])

或者我们仅仅使用A[1:,[1,3]]。还有一种方法是通过矩阵向量积(叉积)。

>>> A[ix_((1,2),(1,3))]
array([[ 5, 7],
[ 9, 11]])

为了读者的方便，在次写下之前的矩阵：

>>> A[ix_((1,2),(1,3))]
array([[ 5, 7],
[ 9, 11]])

现在让我们做些更复杂的。比如说我们想要保留第一行大于1的列。一种方法是创建布尔索引：

>>> A[0,:]>1
array([False, False, True, True], dtype=bool)
>>> A[:,A[0,:]>1]
array([[ 2, 3],
[ 6, 7],
[10, 11]])

就是我们想要的！但是索引矩阵没这么方便。

>>> M[0,:]>1
matrix([[False, False, True, True]], dtype=bool)
>>> M[:,M[0,:]>1]
matrix([[2, 3]])

这个过程的问题是用“矩阵切片”来切片产生一个矩阵12，但是矩阵有个方便的A属性，它的值是数组呈现的。所以我们仅仅做以下替代：

>>> M[:,M.A[0,:]>1]
matrix([[ 2, 3],
[ 6, 7],
[10, 11]])

如果我们想要在矩阵两个方向有条件地切片，我们必须稍微调整策略，代之以：

>>> A[A[:,0]>2,A[0,:]>1]
array([ 6, 11])
>>> M[M.A[:,0]>2,M.A[0,:]>1]
matrix([[ 6, 11]])

我们需要使用向量积ix_:

>>> A[ix_(A[:,0]>2,A[0,:]>1)]
array([[ 6, 7],
[10, 11]])
>>> M[ix_(M.A[:,0]>2,M.A[0,:]>1)]
matrix([[ 6, 7],
[10, 11]])

4、NumPy：初学者绝对基础知识

官网文档：https://numpy.org/doc/stable/user/absolute_beginners.html

欢迎来到NumPy!

安装NumPy

如何导入NumPy

阅读示例代码

Python列表和NumPy数组的区别是什么?

什么是数组?

关于数组的更多信息

如何创建一个基本数组

添加、删除和排序元素

如何知道数组的形状和大小?

你能重塑一个数组吗?

如何将1D数组转换为2D数组(如何向数组添加新轴)

索引和切片

如何从现有数据创建数组

基本数组操作

广播

更多有用的数组操作

创建矩阵

生成随机数

如何获得独特的物品和计数

矩阵的转置和重塑

如何反转一个数组

重塑和扁平化多维数组

如何访问文档字符串以获取更多信息

使用数学公式

如何保存和加载NumPy对象

导入导出CSV文件

使用Matplotlib绘制数组

1. Welcome to NumPy!
2. Installing NumPy
3. How to import NumPy
4. Reading the example code
5. What’s the difference between a Python list and a NumPy array?
6. What is an array?
7. More information about arrays
8. How to create a basic array
9. Adding, removing, and sorting elements
10. How do you know the shape and size of an array?
11. Can you reshape an array?
12. How to convert a 1D array into a 2D array (how to add a new axis to an array)
13. Indexing and slicing
14. How to create an array from existing data
15. Basic array operations
16. Broadcasting
17. More useful array operations
18. Creating matrices
19. Generating random numbers
20. How to get unique items and counts
21. Transposing and reshaping a matrix
22. How to reverse an array
23. Reshaping and flattening multidimensional arrays
24. How to access the docstring for more information
25. Working with mathematical formulas
26. How to save and load NumPy objects
27. Importing and exporting a CSV
28. Plotting arrays with Matplotlib

1. 欢迎来到NumPy!
2. 安装NumPy
3. 如何导入NumPy
4. 阅读示例代码
5. Python列表和NumPy数组的区别是什么?
6. 什么是数组?
7. 关于数组的更多信息
8. 如何创建一个基本数组
9. 添加、删除和排序元素
10. 如何知道数组的形状和大小?
11. 你能重塑一个数组吗?
12. 如何将1D数组转换为2D数组(如何向数组添加新轴)
13. 索引和切片
14. 如何从现有数据创建数组
15. 基本数组操作
16. 广播
17. 更多有用的数组操作
18. 创建矩阵
19. 生成随机数
20. 怎样得到 唯一的 items 和 counts
21. 矩阵的转置和重塑
22. 如何反转一个数组
23. 重塑和扁平化多维数组
24. 如何访问文档字符串以获取更多信息
25. 使用数学公式
26. 如何保存和加载NumPy对象
27. 导入导出CSV文件
28. 使用Matplotlib绘制数组