A*算法之八数码问题（java代码）

一、问题描述

     一个九宫格，有八个数字1-8已经确定位置，剩下一个空格以0表示，0可以和上下左右的数字交换位置。如果给定一个初始状态，一个目标状态，求解从初始状态到目标状态最少要移动多少步

二、算法

      公式表示为： f(n)=g(n)+h(n),其中：

• f(n) 是从初始状态经由状态n到目标状态的代价估计，称作估计函数
• g(n) 是在状态空间从初始状态到状态n的实际代价，称作节点深度（例子中是当前执行了几步）
• h(n) 是从状态n到目标状态的的估计代价，称作启发函数（例子中是当前状态和目标状态有几个数字位置是不一致的，比如初始状态1，2，8和目标状态不一致，0代表空格不算，所以h=3）

举个例子：

（图中启发函数h（x）按与目标状态不一样的个数来计算）

三、算法及步骤

1.设计八数码节点状态结构

存储结构采取一维数组int[] num，估计函数f(n)、节点深度d(n)、启发函数h(n)，以及要定义每一个状态的父状态。 这里额外设置了一个answer的线性表，用于存储最终答案路径（为什么额外设计它后面会解释）后面的getter和setter不额外截图了

2.可达性判断函数设计

这里是通过计算八数码节点的逆序数判断，两个节点状态的逆序数必须同奇或者同偶才是可达状态（也就是初始状态的逆序数+目标状态的逆序数=偶数）。什么是逆序数呢？     如果一对数的前后位置与大小顺序相反，也就是如果较大的数在较小的数之前，那么就算一个逆序对，逆序数+1。逆序数是偶数的排列称作偶排列，是奇数的排列称作奇排列。如在 2,4,3,1 中，21，43，41，31是逆序，逆序数是4，是偶排列。计算八数码节点的逆序数时必须要把代表空格的0去掉，这里是原博客没有注意的地方，判断可达性的函数修改如下：

3.估价函数设计

    估计函数是由两部分构成的，节点深度d(n)其实就是当前已经走的步数，不用额外设计函数；启发函数h(n)是比较重要的一个部分，启发函数的设计直接影响了估计函数的效率，有几种定义方法：

• 当前节点与目标节点差异的度量 => 当前结点与目标节点相比，位置不符的数字个数
• 当前节点与目标节点距离的度量 => 当前结点与目标节点格局位置不符的数字移动到目标节点中对应位置的最短距离之和
• 每一对逆序数字的某倍数 位置不符的数字个数的总和+逆序数的三倍

这里选择的是第一种，计算当前节点与目标节点相比，有多少个数字的位置不符

4.A*算法

依照上面算法流程图设计就可以了。额外需要注意的是： open表和close表使用ArrayList保存状态，open表存放所有的状态，close表则存放在搜索过程中一些较优的状态，但是close表并不是最终我们走的路径。因为我们要在搜索完成找到目标状态之后，根据父状态还原出原路径，因此原博客中的算法只能逆序输出路径。所以我额外设计了一个线性表answer就是为了在还原过程中保存我们所走的路径，从而实现正序的输出。对输出路径的函数修改：

三、代码

package com.hyh.java_algorithm;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Scanner;

@SuppressWarnings("rawtypes")
public class EightPuzzle implements Comparable{
    private int[] num = new int[9];
    private int evaluation;                //估计函数f(n)：从起始状态到目标的最小估计值
    private int depth;                    //d(n)：当前的深度，即走到当前状态的步骤
    private int misposition;            //启发函数 h(n)：到目标的最小估计(记录和目标状态有多少个数不同)
    private EightPuzzle parent;            //当前状态的父状态
    private ArrayList answer = new ArrayList();    //保存最终路径
    public int[] getNum() {
        return num;
    }
    public void setNum(int[] num) {
        this.num = num;
    }
    public int getDepth() {
        return depth;
    }
    public void setDepth(int depth) {
        this.depth = depth;
    }
    public int getEvaluation() {
        return evaluation;
    }
    public void setEvaluation(int evaluation) {
        this.evaluation = evaluation;
    }
    public int getMisposition() {
        return misposition;
    }
    public void setMisposition(int misposition) {
        this.misposition = misposition;
    }
    public EightPuzzle getParent() {
        return parent;
    }
    public void setParent(EightPuzzle parent) {
        this.parent = parent;
    }

    /**
     * 判断当前状态是否为目标状态
     * @param target
     * @return
     */
    public boolean isTarget(EightPuzzle target){
        return Arrays.equals(getNum(), target.getNum());
    }

    /**
     * 求估计函数f(n) = g(n)+h(n);
     * 初始化状态信息
     * @param target
     */
    public void init(EightPuzzle target){
        int temp = 0;
        for(int i=0;i<9;i++){
            if(num[i]!=target.getNum()[i])
                temp++;            //记录当前节点与目标节点差异的度量
        }
        this.setMisposition(temp);
        if(this.getParent()==null){
            this.setDepth(0);    //初始化步数（深度）
        }else{
            this.depth = this.parent.getDepth()+1;//记录步数
        }
        this.setEvaluation(this.getDepth()+this.getMisposition());//返回当前状态的估计值
    }

    /**
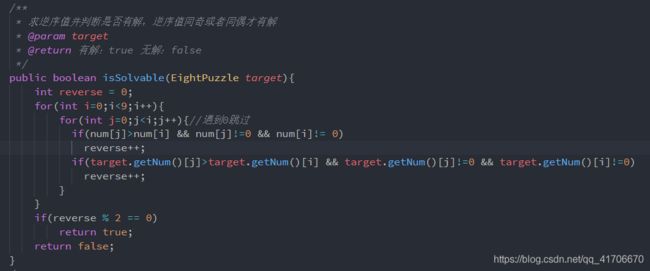
     * 求逆序值并判断是否有解，逆序值同奇或者同偶才有解
     * @param target
     * @return 有解：true 无解：false
     */
    public boolean isSolvable(EightPuzzle target){
        int reverse = 0;
        for(int i=0;i<9;i++){
            for(int j=0;jnum[i] && num[j]!=0 && num[i]!= 0)
                    reverse++;
                if(target.getNum()[j]>target.getNum()[i] && target.getNum()[j]!=0 && target.getNum()[i]!=0)
                    reverse++;
            }
        }
        if(reverse % 2 == 0)
            return true;
        return false;
    }
    /**
     * 对每个子状态的f(n)进行由小到大排序
     * */
    @Override
    public int compareTo(Object o) {
        EightPuzzle c = (EightPuzzle) o;
        return this.evaluation-c.getEvaluation();//默认排序为f(n)由小到大排序
    }
    /**
     * @return 返回0在八数码中的位置
     */
    public int getZeroPosition(){
        int position = -1;
        for(int i=0;i<9;i++){
            if(this.num[i] == 0){
                position = i;
            }
        }
        return position;
    }
    /**
     * 去重，当前状态不重复返回-1
     * @param open    状态集合
     * @return 判断当前状态是否存在于open表中
     */
    public int isContains(ArrayList open){
        for(int i=0; i=6){
            return false;
        }
        return true;
    }
    /**
     *
     * @return 0，3，6（第一列）返回false
     */
    public boolean isMoveLeft() {
        int position = getZeroPosition();
        if(position%3 == 0){
            return false;
        }
        return true;
    }
    /**
     *
     * @return 2，5，8（第三列）不能右移返回false
     */
    public boolean isMoveRight() {
        int position = getZeroPosition();
        if((position)%3 == 2){
            return false;
        }
        return true;
    }
    /**
     *
     * @param move 0：上，1：下，2：左，3：右
     * @return 返回移动后的状态
     */
    public EightPuzzle moveUp(int move){
        EightPuzzle temp = new EightPuzzle();
        int[] tempnum = num.clone();
        temp.setNum(tempnum);
        int position = getZeroPosition();    //0的位置
        int p=0;                            //与0换位置的位置
        switch(move){
            case 0:
                p = position-3;
                temp.getNum()[position] = num[p];
                break;
            case 1:
                p = position+3;
                temp.getNum()[position] = num[p];
                break;
            case 2:
                p = position-1;
                temp.getNum()[position] = num[p];
                break;
            case 3:
                p = position+1;
                temp.getNum()[position] = num[p];
                break;
        }
        temp.getNum()[p] = 0;
        return temp;
    }
    /**
     * 按照3*3格式输出
     */
    public void print(){
        for(int i=0;i<9;i++){
            if(i%3 == 2){
                System.out.println(this.num[i]);
            }else{
                System.out.print(this.num[i]+"  ");
            }
        }
    }
    /**
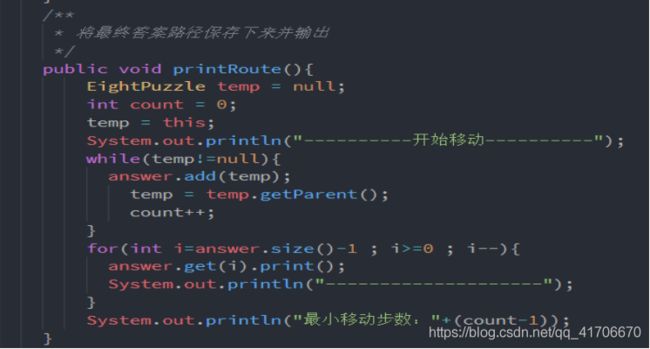
     * 将最终答案路径保存下来并输出
     */
    public void printRoute(){
        EightPuzzle temp = null;
        int count = 0;
        temp = this;
        System.out.println("----------开始移动----------");
        while(temp!=null){
            answer.add(temp);
            temp = temp.getParent();
            count++;
        }
        for(int i=answer.size()-1 ; i>=0 ; i--){
            answer.get(i).print();
            System.out.println("--------------------");
        }
        System.out.println("最小移动步数："+(count-1));
    }
    /**
     *
     * @param open open表
     * @param close close表
     * @param parent 父状态
     * @param target 目标状态
     */
    public void operation(ArrayList open,ArrayList close,EightPuzzle parent,EightPuzzle target){
        if(this.isContains(close) == -1){//如果不在close表中
            int position = this.isContains(open);//获取在open表中的位置
            if(position == -1){//如果也不在open表中
                this.parent = parent;//指明它的父状态
                this.init(target);//计算它的估计值
                open.add(this);//把它添加进open表
            }else{//如果它在open表中
                if(this.getDepth() < open.get(position).getDepth()){//跟已存在的状态作比较，如果它的步数较少则是较优解
                    open.remove(position);//把已经存在的相同状态替换掉
                    this.parent = parent;
                    this.init(target);
                    open.add(this);
                }
            }
        }
    }

    @SuppressWarnings("unchecked")
    public static void main(String args[]){
        //定义open表
        ArrayList open = new ArrayList();
        ArrayList close = new ArrayList();
        EightPuzzle start = new EightPuzzle();
        EightPuzzle target = new EightPuzzle();

//        int stnum[] = {8,6,7,2,5,4,3,0,1};
//        int tanum[] = {6,4,7,8,5,0,3,2,1};

        Scanner s = new Scanner(System.in);
        int stnum[] = new int[9];
        int tanum[] = new int[9];
        System.out.println("请输入初始状态：");
        for(int i = 0; i< 9; i++){
            stnum[i] = s.nextInt();
        }
        System.out.println("请输入目标状态：");
        for(int j= 0; j< 9; j++){
            tanum[j] = s.nextInt();
        }
        s.close();

        start.setNum(stnum);
        target.setNum(tanum);
        long startTime=System.currentTimeMillis();
        if(start.isSolvable(target)){
            //初始化初始状态
            start.init(target);
            open.add(start);
            while(open.isEmpty() == false){
                Collections.sort(open);            //按照evaluation的值排序
                EightPuzzle best = open.get(0);    //从open表中取出最小估值的状态并移出open表
                open.remove(0);
                close.add(best);

                if(best.isTarget(target)){
                    //输出
                    best.printRoute();
                    long end=System.currentTimeMillis();
                    System.out.println("程序运行 "+ (end-startTime) +" ms");
                    System.exit(0);
                }

                int move;
                //由best状态进行扩展并加入到open表中
                //0的位置上移之后状态不在close和open中设定best为其父状态，并初始化f(n)估值函数
                if(best.isMoveUp()){//可以上移的话
                    move = 0;//上移标记
                    EightPuzzle up = best.moveUp(move);//best的一个子状态
                    up.operation(open, close, best, target);
                }
                //0的位置下移之后状态不在close和open中设定best为其父状态，并初始化f(n)估值函数
                if(best.isMoveDown()){
                    move = 1;
                    EightPuzzle down = best.moveUp(move);
                    down.operation(open, close, best, target);
                }
                //0的位置左移之后状态不在close和open中设定best为其父状态，并初始化f(n)估值函数
                if(best.isMoveLeft()){
                    move = 2;
                    EightPuzzle left = best.moveUp(move);
                    left.operation(open, close, best, target);
                }
                //0的位置右移之后状态不在close和open中设定best为其父状态，并初始化f(n)估值函数
                if(best.isMoveRight()){
                    move = 3;
                    EightPuzzle right = best.moveUp(move);
                    right.operation(open, close, best, target);
                }

            }
        }else{
            System.out.println("目标状态不可达");
        }
    }
}