多重网格法（multigrid）求解1d泊松方程--python

教程参考
http://bender.astro.sunysb.edu/classes/numerical_methods/lectures/elliptic-multigrid.pdf
http://staff.ustc.edu.cn/~humaobin/course/cht/ppt/8.7.pdf
直接上代码

import math
import numpy as np  
import matplotlib.pyplot as plt

def coarsen(grid_fine,x_fine):# Lagrange type interpolation, two order

    n_grid_coarsen  =  int(grid_fine.size/2)
    grid_coarsen  =  np.zeros(n_grid_coarsen,  dtype   =   float)
    x_coarsen = np.linspace(x_fine[0],x_fine[-1],n_grid_coarsen)

    for i in range(1, grid_coarsen.size):
        # print(grid_coarsen.size, i)
        i2  = np.count_nonzero(x_fine<x_coarsen[i])-1# find the index in x_fine
        
        l0  =  (x_coarsen[i]-x_fine[i2])*(x_coarsen[i]-x_fine[i2+1])/(x_fine[i2-1]-x_fine[i2])/(x_fine[i2-1]-x_fine[i2+1])
        l1  =  (x_coarsen[i]-x_fine[i2-1])*(x_coarsen[i]-x_fine[i2+1])/(x_fine[i2]-x_fine[i2-1])/(x_fine[i2]-x_fine[i2+1])
        l2  =  (x_coarsen[i]-x_fine[i2-1])*(x_coarsen[i]-x_fine[i2])/(x_fine[i2+1]-x_fine[i2-1])/(x_fine[i2+1]-x_fine[i2])
        
        grid_coarsen[i]  =  l0*grid_fine[i2-1] + l1*grid_fine[i2] +l2*grid_fine[i2 + 1]#Lagrange type interpolation

    grid_coarsen[0]  =  grid_fine[0]#left_boundary
    grid_coarsen[-1]  =  grid_fine[-1]#right_boundary
    return grid_coarsen, x_coarsen
def fine(grid_coarsen,x_coarsen): #

    n_grid_fine  =  int(grid_coarsen.size*2)
    grid_fine  =  np.zeros(n_grid_fine,  dtype   =   float)
    x_fine  =  np.linspace(x_coarsen[0], x_coarsen[-1],n_grid_fine)
    for i in range(1, grid_fine.size):

        if x_fine[i] > x_coarsen[1]:
            i2 = np.count_nonzero(x_coarsen<x_fine[i])-1#find the index 

            l0  =  (x_fine[i]-x_coarsen[i2])*(x_fine[i]-x_coarsen[i2+1])/(x_coarsen[i2-1]-x_coarsen[i2])/(x_coarsen[i2-1]-x_coarsen[i2+1])
            l1  =  (x_fine[i]-x_coarsen[i2-1])*(x_fine[i]-x_coarsen[i2+1])/(x_coarsen[i2]-x_coarsen[i2-1])/(x_coarsen[i2]-x_coarsen[i2+1])
            l2  =  (x_fine[i]-x_coarsen[i2-1])*(x_fine[i]-x_coarsen[i2])/(x_coarsen[i2+1]-x_coarsen[i2-1])/(x_coarsen[i2+1]-x_coarsen[i2])
        
            grid_fine[i]  =  l0*grid_coarsen[i2-1] + l1*grid_coarsen[i2] +l2*grid_coarsen[i2 + 1]#Lagrange type interpolation
        else:
            l0  =  (x_fine[i]-x_coarsen[1])/(x_coarsen[0]-x_coarsen[1])
            l1  =  (x_fine[i]-x_coarsen[0])/(x_coarsen[1]-x_coarsen[0])
            grid_fine[i]  =  l0*grid_coarsen[0]+l1*grid_coarsen[1]
    grid_fine[0]  =  grid_coarsen[0]#left_boundary
    grid_fine[-1]  =  grid_coarsen[-1]#right_boundary

    return grid_fine, x_fine
    
def Relax2( b,  phi,  h,leveli):
    om  =  1.95
    ite  =  3**leveli    # the iteration increase with the level to get higher precision
    j   =   0
 
    while(j <ite): #控制迭代次数
        i   =   1                    # when the boundary is known,  set i   =   1
        while( i < phi.size-1):  
            phi_i  =  np.copy(phi[i])
            phi[i]  =  (1.-om)*phi_i+om*0.5*(phi[i + 1] + phi[i-1]-(h*h)*b[i])
            i   =   i + 1
        j   =   j + 1
    return phi

def residual(f, u, h):
    r  =  np.zeros(f.size,  dtype   =   float)
    for i in range(1, u.size-1):
        r[i]  =  f[i]*(h*h)-(u[i + 1]-2.*u[i] + u[i-1])
    return r

def fbh(x):
    b = -64*np.sin(8*x) 
    return b
def MG2(phi, x, b):

    h0  =  x[1]-x[0]               
    vh0  =  Relax2(b, phi, h0,1)
    rh  =  residual(b, vh0, h0)# residual
    eh0 = np.zeros(rh.size,dtype = float)
    eh =  Relax2(rh, eh0,  h0,1)
    vh = vh0+eh
    rh  =  residual(b, vh, h0)

    t = 0

    while ((np.max(rh) > 1e-2) and (t < 10)): 
        for i in range(1,5): 
            k = i
            r2h,x2 =  coarsen(rh,x)   # residual to fine grid
            e2h0 = np.zeros(r2h.size,dtype = float)
            h2  =  x2[2]-x2[1]
            e2h  =  Relax2(r2h, e2h0,  h2,k)
            print(vh.size,x.size)
            v2h,x2 = coarsen(vh,x)
            phi = v2h+e2h
            b = fbh(x2)
            vh =  Relax2(b, phi, h2,k)
            rh = residual(b, vh, h2)
            x = x2
        for i in range(1,5): 
            k = 6-i

            r2h,x2 =  fine(rh,x)   # residual to fine grid
            e2h0 = np.zeros(r2h.size,dtype = float)# initiate the err
            h2  =  x2[2]-x2[1]
            e2h  =  Relax2(r2h, e2h0,  h2,k)     #calculate err
            print(vh.size,x.size)
            v2h,x2 = fine(vh,x)                  #to fine grid
            phi = v2h+e2h                        # update phi
            b = fbh(x2)                          # calculate b on this level
            vh =  Relax2(b, phi, h2,k)           # calculate  vh again with updated phi
            rh = residual(b, vh, h2)             #calculate residual
            x = x2
        t = t+1
        print(t)
    return vh,x2

n_grid  =  128#should be 2**n
xs  =  0.0
xe  =  math.pi
x = np.linspace(xs,xe,n_grid)
h = x[1]-x[0]
phi   =   np.ones(x.size,  dtype   =   float)*0.1
phi[0]  =  0.
phi[-1]  =  0.

b  =  -64*np.sin(8*x)#泊松方程，b是二阶导数的值。泊松方程形式phi''=b
  #precise solution
result,x2  =  MG2(phi, x, b)
result2  =  np.sin(8*x2) 

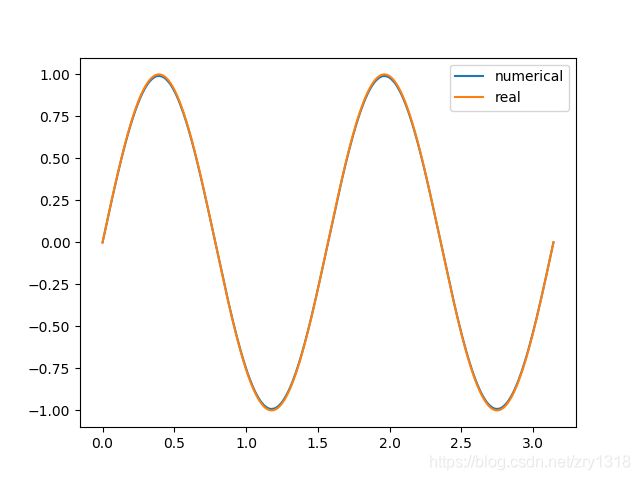
plt.figure(1)
plt.plot(x2, result2, label  =  'original')
plt.scatter(x2, result, label  =  'simulation')
plt.legend()
plt.show()
plt.close()

结果如图