matlab中用simulink仿真六足机器人

1.开篇之言

因为六足机器人在simulink中仿真目前告一段落，所以记录一下这个过程，有的介绍并不详细，只是大概记录过程，方便以后回忆使用，仿真还是因为疫情期间无法回校，在家只能进行仿真喽，我想开学，我想开学，我想开学，我想回校，我想回校，我想回校！！！哎，人生苦短，多多熬夜！！！

2.simulink中导入.urdf文件

1.安装插件Simscape
下载地址：https://ww2.mathworks.cn/products/simmechanics/download_smlink_confirmation.html?elqsid=1482376811915&potential_use=Education

（1）下载对应版本，下载好后如下图所示：

（2）打开MATLAB，选择当前文件夹为下载的安装包路径，在命令行窗口输入如下命令：
install_addon(‘smlink.r2018b.win64.zip’)

（3）导入.urdf格式文件
这个文件由于是队友弄的，在此不介绍了，只知道是在Solidwork中搞的，导出这个格式需要在Solidwork中安装一个插件

选择当前文件夹为包含此格式路径，在命令行窗口输入如下命令： smimport(‘xxxxx.urdf’)

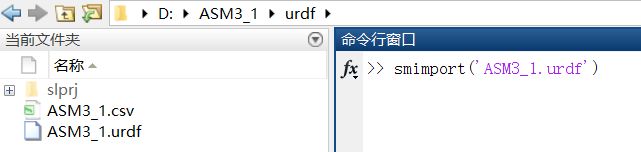
导入过程挺慢的，应该大概一分多钟吧，成功导入显示如下：

3.给模型添加模块

导入后的模型需要添加 “地面”，“六自由度”，“足尖与地面接触”
添加后的图片如下：

其中“足尖与地面接触”这个模块需要安装一个功能包才能找到：（模块专业名字：Sphere to Plane Force）
如何安装这个功能包呢？如下：
（1）在matlab主页中点附加功能–获取附加功能

（2）在simulink中一列中找到如下功能包：

（3）Simscape-Multibody-Contact-Forces-Library功能包可以直接下载安装，我这出了点问题，我是先下载好（选择相应的版 本），然后设置matlab默认搜索路径，方法如下：
点击 设置路径

再点击 添加并包含子文件夹找到Simscape-Multibody-Contact-Forces-Library的放置路径（最好把下载好的文件放在matlab安装目录下的toolbox文件夹下）
这样就可以再Simulink Library Browser（就是那个四个正方形的图标）里找到Simscape-Multibody-Contact-Forces-Library了
不过要调节Sphere to Plane Force里的参数，可以参考这个模块的帮助文档，这个调参挺悬乎，搞了好久
（4）点击仿真，效果如下：

4.正/逆运动学的研究

（1）我们是现在matlab中简单建立一个三自由度的机械臂来研究逆运动学，这前提需要安装机器人工具箱：

下载地址：http://petercorke.com/wordpress/toolboxes/robotics-toolbox#Downloading_the_Toolbox

下载解压，剪切到matlab安装目录下的toolbox文件夹，打开matlab的设置路径，点击添加子文件夹（同上）

（2）建立机器人模型
下面分享三段代码，队友搞的：
第一段代码（niyundongxue）：逆运动学代码，由于我们求逆解是用的几何法，所以只要长度参数改变，都需要改动代码：

function Theta = niyundongxue(A)
L1 = 0.66;     % 六足退第一段长度   
L2 = 0.94;     % 六足退第二段长度 
L3 = 1.43;     % 六足退第三段长度 

x = A(1,4);    % 变换矩阵中取x坐标
y = A(2,4);    % 变换矩阵中取y坐标
z = A(3,4);    % 变换矩阵中取z坐标

if (y==0)
    q1 = 0 ;
else 
    q1 =atan(y/(x-1.16)) ;                                          % q1是第一个舵机转动角度
end

X=x-1.16-L1*cos(q1);
Y= y-L1*sin(q1);
L = ( X^2 + Y^2  + z^2 )^0.5 ;
    
q2 = acos((L2^2+L^2-L3^2)/(2*L2*L)) +  atan(z/(X^2+Y^2)^0.5) ;      % q2是第二个舵机转动角度

q3 = -pi+acos((L2^2+L3^2-L^2)/(2*L2*L3));                           % q3是第三个舵机转动角度

第二段代码（demo）：建立简单模型代码，并验证逆运动学代码的正确性：

L(1)=Link([0 0 1.16 0],'modified');     % D-H参数 建立连杆
L(2)=Link([0 0 0.66 pi/2],'modified');  % D-H参数 建立连杆
L(3)=Link([0 0 0.94 0],'modified');     % D-H参数 建立连杆
L(4)=Link([0 0 1.43 0],'modified');     % D-H参数 建立连杆
Six_Food=SerialLink([L(1),L(2),L(3),L(4)]);   % 建立机器人
SixFood.name='Six_Food';
T5=[pi/3 pi/10 -pi/1.5 0];    % 给定角度，先用正运动学
ts = T5*180/pi;

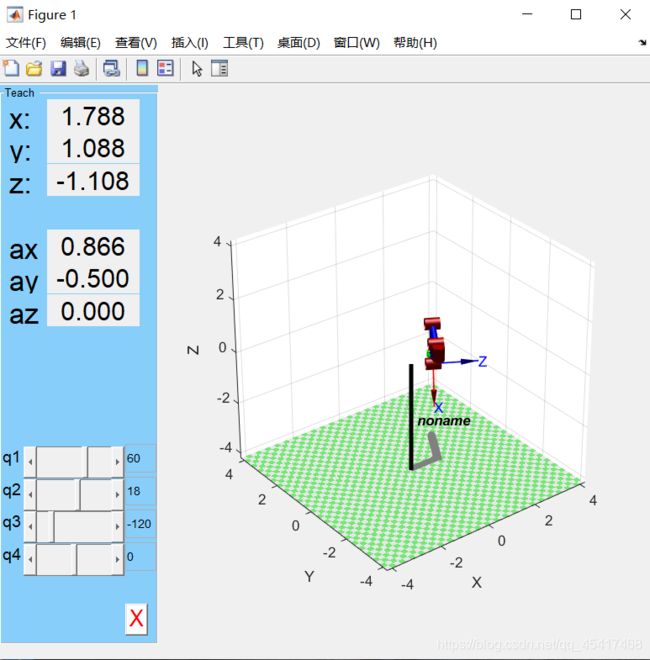
Six_Food.plot(T5);       % 画出图像
Six_Food.teach;          % 调出控制选型

T6 = Six_Food.fkine(T5); % 正运动学求齐次变换矩阵
T7 = niyundongxue(T6);   % 逆运动学求各个关节角度

disp(T6);                % 显示齐次变换矩阵
disp(ts);                % 显示给定角度的角度制
disp(T5);                % 显示给定角度
disp(T7);                % 显示逆运动学求出的角度

demo代码运行结果如下：

demo代码运行图如下：

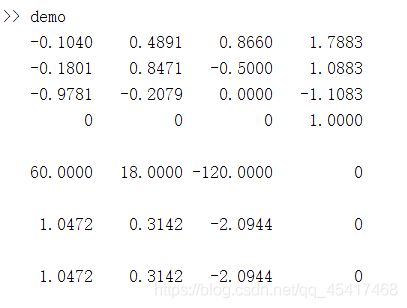
然后令A= [-0.1040 0.4891 0.8660 1.7883
-------------- -0.1801 0.8471 -0.5000 1.0883
-------------- -0.9781 -0.2079 0.0000 -1.1083
----------------------- 0 --------- 0 ------- 0 1.0000] （ A等于上面求出来的齐次变换矩阵）
然后运行niyundongxue代码，结果如下：

可以证明队友写的逆运动学的正确性！！

第三段代码（Hexapod_Food）：可以显示运动轨迹，速度，加速度等等

L(1)=Link([0 0 1.16 0],'modified');
L(2)=Link([0 0 0.66 pi/2],'modified');
L(3)=Link([0 0 0.94 0],'modified');
L(4)=Link([0 0 1.43 0],'modified');
Six_Food=SerialLink([L(1),L(2),L(3),L(4)]);
SixFood.name='Six_Food';
% Six_Food.plot([0 0 -pi/2 0;0 0 0 0]);       %画出图像
% Six_Food.teach;                     %调出控制选型
Six_Food.display();


First_Theta = [pi/3 pi/6  -pi/1.8 0 ];
Final_Theta = [-pi/3 pi/6 -pi/1.8 0] ;              %   [pi/4 pi/8 -pi/4 0];
step = 666;
[q,qd,qdd] = jtraj(First_Theta,Final_Theta,step);
 
subplot(2,4,1);
i = 1:4;
plot(q(:,i));
grid on;
title('位置');  
 
subplot(2,4,2);
i = 1:4;
plot(qd(:,i));grid on;
title('速度');
    
subplot(2,4,5);
i = 1:4;
plot(qdd(:,i));grid on;
title('加速度');
    
T0 = Six_Food.fkine(First_Theta);
Tf = Six_Food.fkine(Final_Theta);
    
Tc = ctraj(T0,Tf,step);   
     
Tjtraj = transl(Tc);
       
subplot(2,4,6);
plot2(Tjtraj,'r');grid on;
title('TO到Tf直线轨迹');
    
subplot(2,4,[3,4,7,8]);
   
qq = zeros(4,100);
for Var = 1:666

    qq(:,Var) = niyundongxue(Tc(:,:,Var));
 
end
B = qq';

Six_Food.plot(B);

此代码运行结果如下：（其中运行过程中模型会一点点移动）

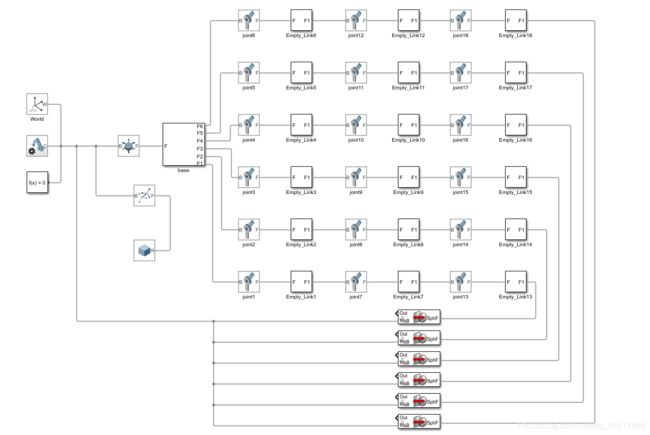
5.移植实体模型

最后就是再逆运动学的基础上加一些其他代码来实现每个功能：
下面是大致simulink图：

具体怎么来，各位探索吧，在这不说了！！！！！！

6.结尾

最后以一张图结尾吧

7.彩蛋

由于能力有限，下面写一些自己看的链接：

机器人工具箱：常用函数

链接：https://blog.csdn.net/xuehuafeiwu123/article/details/52787080

机器人工具箱：建立简单机器人模型

链接：https://blog.csdn.net/xuehuafeiwu123/article/details/52549878

机器人工具箱：正/逆运动学

链接：https://blog.csdn.net/xuehuafeiwu123/article/details/52668916

机器人工具箱：轨迹的规划

链接：https://blog.csdn.net/xuehuafeiwu123/article/details/52672892