A*算法简介

A*算法是一种启发式的搜索算法， A*算法在某种程度上和广度优先搜索（ BFS）、 深度优先搜索（ DFS） 类似， 都是按照一定的原则确定如何展开搜索的节点树状结构。 A*可以认为是一种基于“ 优点” 的搜索算法。

搜索区域(The Search Area)：

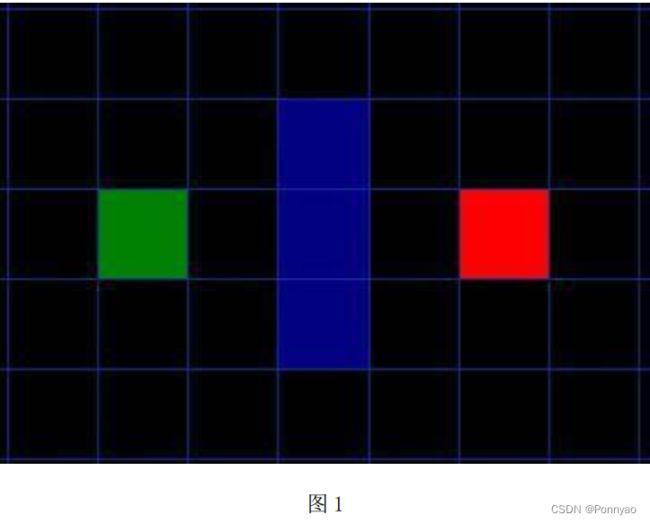
我们假设某人要从 A 点移动到 B 点， 但是这两点之间被一堵墙隔开。 如图 1 ，绿色是 A ， 红色是 B ， 中间蓝色是墙。

你应该注意到了， 我们把要搜寻的区域划分成了正方形的格子。 这是寻路的第一步， 简化搜索区域。 这个特殊的方法把我们的搜索区域简化为了 2 维数组。数 组 的 每 一 项 代 表 一 个 格 子 ， 它 的 状 态 就 是 可 走 (walkalbe) 和 不 可 走(unwalkable)两种。 通过计算出从 A 到 B 需要走过哪些方格， 就找到了路径。 一旦路径找到了， 人物便从一个方格的中心移动到另一个方格的中心， 直至到达目的地。

方格的中心点我们称为“ 节点 (nodes)”。 如果你读过其他关于 A*寻路算法的文章， 你会发现人们常常都在讨论节点。 为什么不直接描述为方格呢？ 因为我们有可能把搜索区域划为其他多变形而不是正方形， 例如可以是六边形， 矩形，甚至可以是任意多变形。 而节点可以放在任意多边形里面， 可以放在多变形的中心， 也可以放在多边形的边上。 我们使用这个系统， 因为它最简单。

开始搜索(Starting the Search)

一旦我们把搜寻区域简化为一组可以量化的节点后， 就像上面做的一样， 我们下一步要做的便是查找最短路径。 在 A*中， 我们从起点开始， 检查其相邻的方格， 然后向四周扩展， 直至找到目标。

我们这样开始我们的寻路旅途：

1.从起点 A 开始， 并把它就加入到一个由方格组成的 open list(开放列表)中。 这个 open list 有点像是一个购物单。 当然现在 open list 里只有一项，它就是起点 A ， 后面会慢慢加入更多的项。 Open list 里的格子是路径可能会是沿途经过的， 也有可能不经过。 基本上 open list 是一个待检查的方格列表。

2.查看与起点 A 相邻的方格 (忽略其中墙壁所占领的方格， 河流所占领的方格及其他非法地形占领的方格) ， 把其中可走的或可到达的方格也加入到open list 中。 把起点 A 设置为这些方格的父亲 (parent node 或 parentsquare) 。 当我们在追踪路径时， 这些父节点的内容是很重要的。 稍后会进行解释。

3.把 A 从 open list 中移除， 加入到 close list(封闭列表) 中， closelist 中的每个方格都是现在不需要再关注的。我们看这张图中， 深绿色的方格为起点， 它的外框是亮蓝色， 表示该方格被加入到了 close list。 与它相邻的黑色方格是需要被检查的， 他们的外框是亮绿色。 每个黑方格都有一个灰色的指针指向他们的父节点， 也就是起点 A。

下一步， 我们需要从 open list 中选一个与起点 A 相邻的方格， 按下面描述的一样或多或少的重复前面的步骤。 但是到底选择哪个方格好呢？ 具有最小 F值的那个。

路径排序(Path Sorting)

计算出组成路径的方格的关键是下面这个等式：

F = G + H

这里， G 表示从起点 A 移动到指定方格的移动代价， 沿着到达该方格而生成的路径。

H 表示从指定的方格移动到终点 B 的估算成本。

这个通常被称为试探法， 有点让人混淆。 为什么这么叫呢， 因为这是个猜测。直到我们找到了路径我们才会知道真正的距离， 因为途中有各种各样的东西 (比如墙壁， 水等)。 这里将教你一种计算 H 的方法。

我们的路径是这么产生的： 反复遍历 open list， 选择 F 值最小的方格。 这个过程稍后详细描述。 我们还是先看看怎么去计算上面的等式。

就像上面所说的， G 是从起点 A 移动到指定方格的移动代价。 在本例中， 横向和纵向的移动代价为 10， 对角线的移动代价为 14。 之所以使用这些数据， 是因为实际的对角移动距离是 2 的平方根， 或者是近似的 1.414 倍的横向或纵向移动代价。 使用 10 和 14 就是为了简单起见。 比例是对的， 我们避免了开方和小数的计算。 这并不是我们没有这个能力或是不喜欢数学。 使用这些数字也可以使计算机更快。 稍后你便会发现， 如果不使用这些技巧， 寻路算法将很慢。

既然我们是沿着到达指定方格的路径来计算 G 值， 那么计算出该方格的 G值的方法就是找出其父亲的 G 值， 然后按父亲是直线方向还是斜线方向加上 10或 14。 随着我们离开起点而得到更多的方格， 这个方法会变得更加明朗。

有很多方法可以估算 H 值。 这里我们使用 Manhattan 方法， 计算从当前方格横向或纵向移动到达目标所经过的方格数， 忽略对角移动， 然后把总数乘以10 。 之所以叫做 Manhattan 方法， 是因为这很像统计从一个地点到另一个地点所穿过的街区数， 而你不能斜向穿过街区。 重要的是， 计算 H 时， 要忽略路径中的障碍物。 这是对剩余距离的估算值， 而不是实际值， 因此才称为试探法。

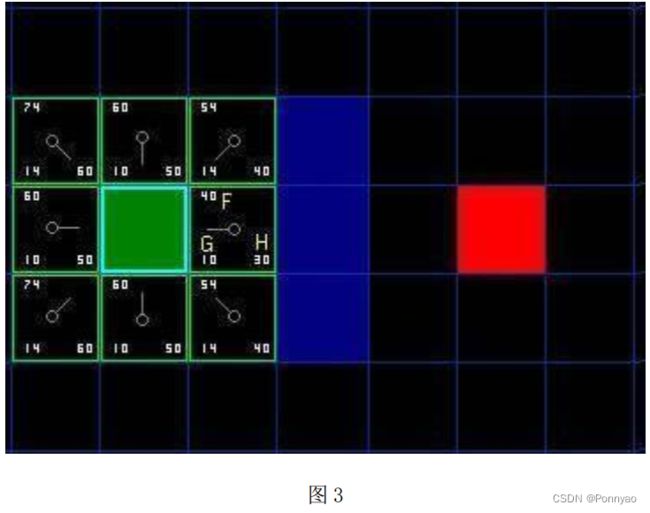
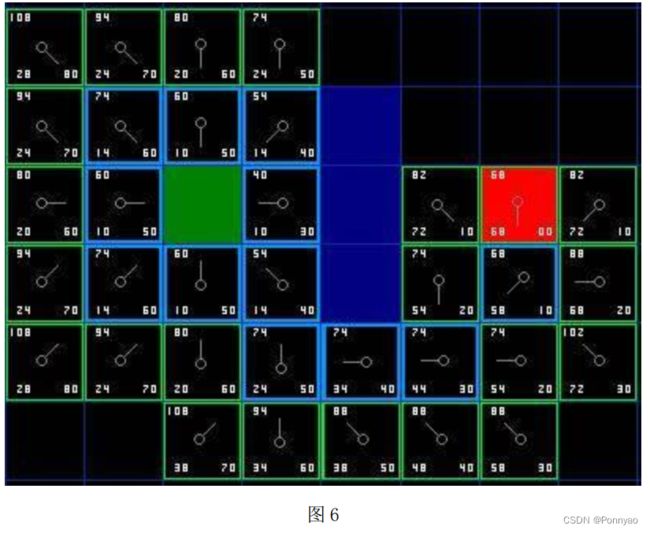
把 G 和 H 相加便得到 F 。 我们第一步的结果就是图片上所示的。 每个方格都标上了 F,G,H 的值， 就像起点右边的方格那样， 左上角是 F ， 左下角是 G ，右下角是 H 。

好， 现在让我们看看其中的一些方格。 在标有字母的方格， G = 10 。 这是因为水平方向从起点到那里只有一个方格的距离。 与起点直接相邻的上方， 下方，左方的方格的 G 值都是 10 ， 对角线的方格 G 值都是 14 。

H 值通过估算起点于终点 ( 红色方格 ) 的 Manhattan 距离得到， 仅作横向和纵向移动， 并且忽略沿途的墙壁。 使用这种方式， 起点右边的方格到终点有3 个方格的距离， 因此 H = 30。 这个方格上方的方格到终点有 4 个方格的距离( 注意只计算横向和纵向距离 ) ， 因此 H = 40。 对于其他的方格， 你可以用同样的方法知道 H 值是如何得来的。

每个方格的 F 值， 再说一次， 直接把 G 值和 H 值相加就可以了。

继续搜索(Continuing the Search)

为了继续搜索， 我们从 open list 中选择 F 值最小的 ( 方格 ) 节点， 然后对所选择的方格这样操作：

1.把它从 open list 里取出， 放到 close list 中。

2. 检 查 所 有 与 它 相 邻 的 方 格 ， 忽 略 其 中 close list 中 或 是 不 可 走(unwalkable) 的方格 (比如墙， 水， 或是其他非法地形)， 如果方格不在 open lsit 中， 则把它们加入到 open list 中。把我们选定的方格设置为这些新加入的方格的父亲。

3.如果某个相邻的方格已经在 open list 中， 则检查这条路径是否更优， 也就是说经由当前方格(我们选中的方格)到达那个方格是否具有更小的 G 值。 如果没有， 不做任何操作。相反， 如果 G 值更小， 则把那个方格的父亲设为当前方格 ( 我们选中的方格 ) ， 然后重新计算那个方格的 F 值和 G 值。 如果你还是很混淆， 请参考下图。

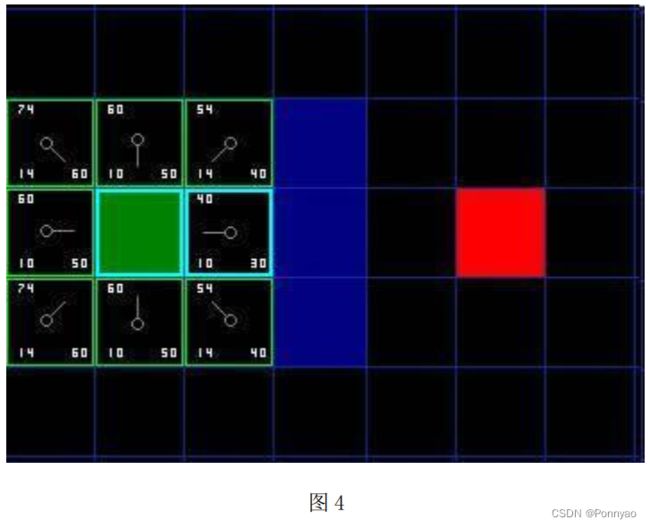
让我们看看它是怎么工作的。 在我们最初的 9 个方格中， 还有 8 个在 open list 中， 起点被放入了 close list 中。 在这些方格中， 起点右边的格子的 F 值40 最小， 因此我们选择这个方格作为下一个要处理的方格。 它的外框用蓝线打亮。

首先， 我们把它从 open list 移到 close list 中 (这也就是为什么用蓝线打亮的原因)。 然后我们检查与它相邻的方格。 它右边的方格是墙壁， 我们忽略。它左边的方格是起点， 在 close list 中， 我们也忽略。 其他 4 个相邻的方格均在 open list 中， 我们需要检查经由这个方格到达那里的路径是否更好， 使用 G值来判定。 让我们看看上面的方格。 它现在的 G 值为 14。 如果我们经由当前方格到达那里， G 值将会为 20(其中 10 为到达当前方格的 G 值， 此外还要加上从当前方格纵向移动到上面方格的 G 值10)。 显然 20 比 14 大， 因此这不是最优的路径。 如果你看图你就会明白。 直接从起点沿对角线移动到那个方格比先横向移动再纵向移动要好。

当把 4 个已经在 open list 中的相邻方格都检查后， 没有发现经由当前方格更好的路径， 因此我们不做任何改变。 现在我们已经检查了当前方格的所有相邻的方格， 并也对他们作了处理， 是时候选择下一个待处理的方格了。

因此再次遍历我们的 open list， 现在它只有 7 个方格了， 我们需要选择 F值最小的那个。 有趣的是， 这次有两个方格的 F 值都是 54， 选哪个呢？ 。 从速度上考虑， 选择最后加入 open list 的方格更快。 这导致了在寻路过程中， 当靠近目标时， 优先使用新找到的方格的偏好。 但是这并不重要。 (对相同数据的不同对待， 导致两中版本的 A*找到等长的不同路径 )。

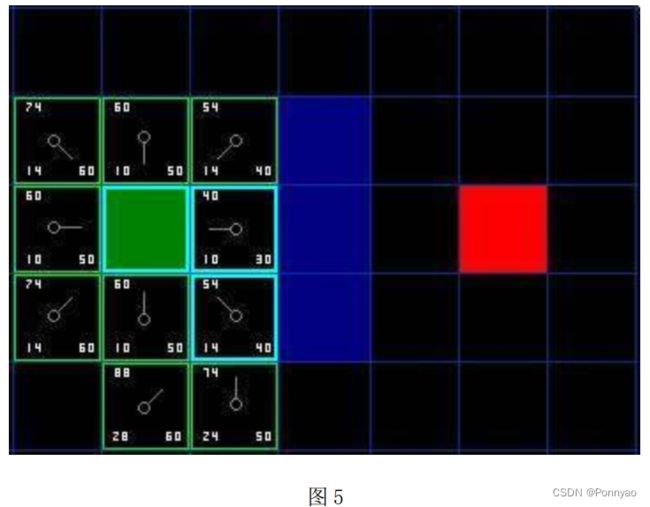
我们选择起点右下方的方格， 如下图所示。

这次， 当我们检查相邻的方格时， 我们发现它右边的方格是墙， 忽略它。 上面的也一样。

我们把墙下面的一格也忽略掉。 为什么？ 因为如果不穿越墙角， 你不能直接从当前方格移动到那个方格。 你需要先往下走， 然后再移动到那个方格， 这样来绕过墙角。 (注意： 穿越墙角的规则是可以选择的， 依赖于你的节点是怎么放置的)

这样还剩下 5 个相邻的方格。当前方格下面的 2 个方格还没有加入 open list，所以把它们加入， 同时把当前方格设为他们的父亲。 在剩下的 3 个方格中， 有 2个已经在 close list 中 (其中一个是起点， 一个是当前方格上面的方格， 外框被加亮的)， 我们忽略它们。 最后一个方格， 也就是当前方格左边的方格， 我们检查经由当前方格到达那里是否具有更小的 G 值， 结果是没有， 因此我们准备从open list 中选择下一个待处理的方格。

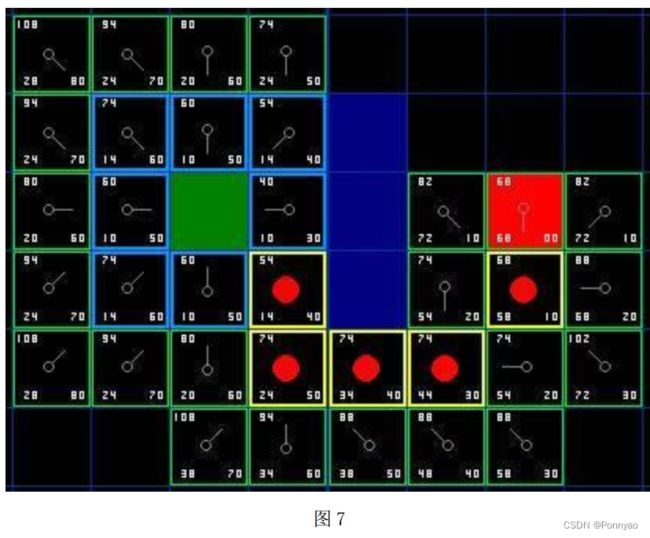
不断重复这个过程， 直到把终点也加入到了 open list 中， 此时如下图所示。

注意， 在起点下面 2 格的方格的父亲已经与前面不同了。 之前它的 G 值是28， 并且指向它右上方的方格。 现在它的 G 值为 20， 并且指向它正上方的方格。这在寻路过程中的某处发生， 使用新路径时 G 值经过检查并且变得更低， 因此父节点被重新设置， G 值和 F 值被重新计算。 尽管这一变化在本例中并不重要， 但是在很多场合中， 这种变化会导致寻路结果的巨大变化。

那么我们怎么样去确定实际路径呢？ 很简单， 从终点开始， 按着箭头向父节点移动， 这样你就被带回到了起点， 这就是你的路径。 就像这张图里， 从起点 A移动到终点 B 就是简单从路径上的一个方格的中心移动到另一个方格的中心， 直至目标。 就是这么简单！