【智能优化算法】猫群优化算法 (Cat Swarm Optimization, CSO),2006
前言
- 猫群优化 (Cat Swarm Optimization, CSO) 算法。由 Chu 和 Tsai 等于 2006 年提出。
- 主要模仿了猫捕捉猎物的行为。

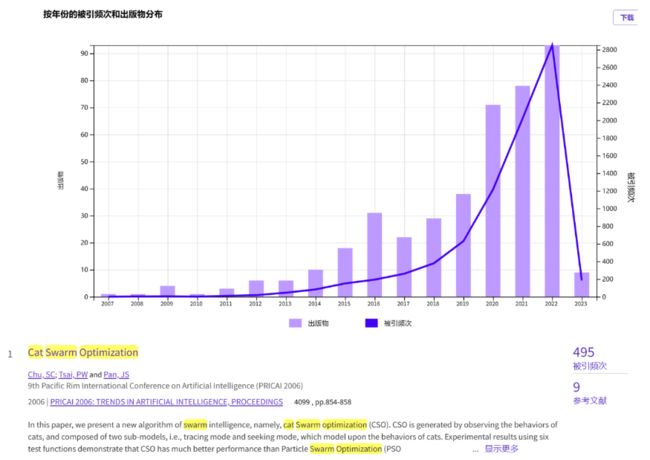
截止到 2023 年,算法引用趋势
1. 猫相关的生物群行为
猫的生活习性?
猫大部分时间都处于休息状态,很少去搜寻和捕捉猎物。但是猫的警觉性非常高,即使在休息的时候也处于一种高度的警惕状态,时刻保持对周围环境的警戒搜寻;它们对于活动的目标具有强烈的好奇心,一旦发现目标便进行跟踪,并且能够迅速地捕获到猎物。
猫的行为模式概括?
- 搜寻模式: 猫在慵懒、环顾四周状态时的模式。
- 跟踪模式: 猫在跟踪猎物目标时的状态。
大致过程如下:
- 根据一定的分组率将猫群分为两个子群,少一部分猫处于跟踪模式,大部分猫处于搜寻模式。
- 搜寻模式 – 全局搜索: 每只猫处于无目的搜寻状态
- 跟踪模式 – 局部搜索: 向全局最优点移动
- 计算所有猫的适应度(捕猎位置优劣)并保留最优值。
- 对猫群重新分配两种模式,进行迭代寻优。
2. 算法仿生设计
搜寻模式用来模拟猫的当前状态,分别为休息、四处查看、搜寻下一个移动位置。在搜寻模式中,定义了 4 个基本要素:记忆池(SMP)、变化域(SRD)、变化数(CDC)、自身位置判断(SPC)。SMP 定义了每一只猫的搜寻记忆大小,表示猫所搜寻到的位置点,猫将根据适应度大小从记忆池中选择一个最好的位置点。SRD 表示选择域的变异率,搜寻模式中,每一维的改变范围由变化域决定,根据经验一般取值为 0.2。CDC 指每一只猫将要变异的维数的个数,其值是一个从 0 到总维数之间的随机值。SPC 是一个布尔值,表示猫是否将已经过的位置作为将要移动到的候选位置之一,其值不影响 SMP 的取值。
2.1 搜寻模式
-
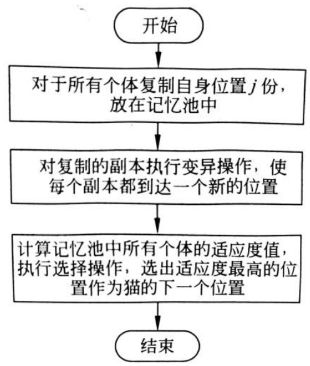
(1) 将当前位置复制 j 份副本放在记忆池中,j = SMP,即记忆池的大小为 j; 如果 SPC 的值为真,令 j = (SMP-1),将当前位置保留为候选解。
-
(2) 对记忆池中的每个个体副本,根据 CDC 的大小,随机地对当前值加上或者减去 SRD (变化域由百分率表示),并用更新后的值来代替原来的值。
-
(3) 分别计算记忆池中所有候选解的适应度值。
-
(4) 从记忆池中选择适应度值最高的候选点来代替当前猫的位置,完成猫的位置更新。
2.2 跟踪模式
跟踪模式用来模拟猫跟踪目标时的情况。通过改变猫的每一维的速度(即特征值)来更新猫的位置,速度的改变是通过增加一个随机的扰动来实现的。
(1) 速度更新。 整个猫群经历过的最好位置,即目前搜索到的最优解,记做 X best \text{X}_\text{best} Xbest. 每只猫的速度记做 v i = v i,1 , v i,2 , . . . , v i,d \text{v}_\text{i} = \text{v}_\text{i,1}, \text{v}_\text{i,2}, ..., \text{v}_\text{i,d} vi=vi,1,vi,2,...,vi,d, 每只猫根据公式 (1) 来更新自己的速度:
v i,d ( t + 1 ) = v i,d ( t ) + r ∗ c ∗ ( X best,d ( t ) − x i,d ( t ) ) , d = 1 , 2 , . . . , M \text{v}_\text{i,d}(t + 1) = \text{v}_\text{i,d}(t) + r * c * (\text{X}_\text{best,d}(t) - \text{x}_\text{i,d}(t)), \text{d} = 1, 2, ..., \text{M} vi,d(t+1)=vi,d(t)+r∗c∗(Xbest,d(t)−xi,d(t)),d=1,2,...,M
式中, v i,d ( t + 1 ) \text{v}_\text{i,d}(t + 1) vi,d(t+1) 表示更新后第 i 只猫在第 d 维的速度值,M 为维度大小; X best,d ( t ) \text{X}_\text{best,d}(t) Xbest,d(t) 表示猫群中当前具有最好适应度值的猫的位置; x i,d \text{x}_\text{i,d} xi,d 指当前第 i 只猫在第 d 维的位置,c 是个常量,其值需要根据不同的问题而定。 r \text{r} r 是一个 [0,1] 之间的随机数。
(2) 判断每一维的速度变化是否都在 SRD 内。 给每一维的变异加一个限制范围,是为了防止其变化过大,造成算法在解空间的盲目随机搜索。SRD 在算法执行之前给定,如果每一维改变后的值超出了 SRD 的限制范围,则将其设定为给定的边界值。
(3) 位置更新。 根据公式 (2) 利用更新后的速度来更新猫的位置。
x i,d ( t + 1 ) = x i,d ( t ) + v i,d ( t + 1 ) , d = 1 , 2 , . . . , M \text{x}_\text{i,d}(t + 1) = \text{x}_\text{i,d}(t) + \text{v}_\text{i,d}(t + 1), \text{d} = 1, 2, ..., \text{M} xi,d(t+1)=xi,d(t)+vi,d(t+1),d=1,2,...,M
式中, x i,d ( t + 1 ) \text{x}_\text{i,d}(t + 1) xi,d(t+1) 表示第 i 只猫更新后的位置。
3. 算法流程
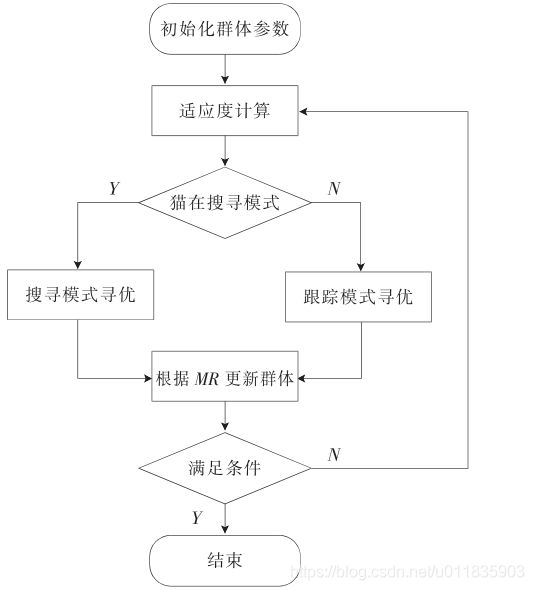
4. 算法特点
- 可以同时进行局部搜索和全局搜索。
- 分组率、搜寻的猫能复制的个体数由人工设置,对算法性能影响较大。
- 搜寻模式中没有使用群体信息,每只猫完全自由变异找寻最佳位置,随机性太大。
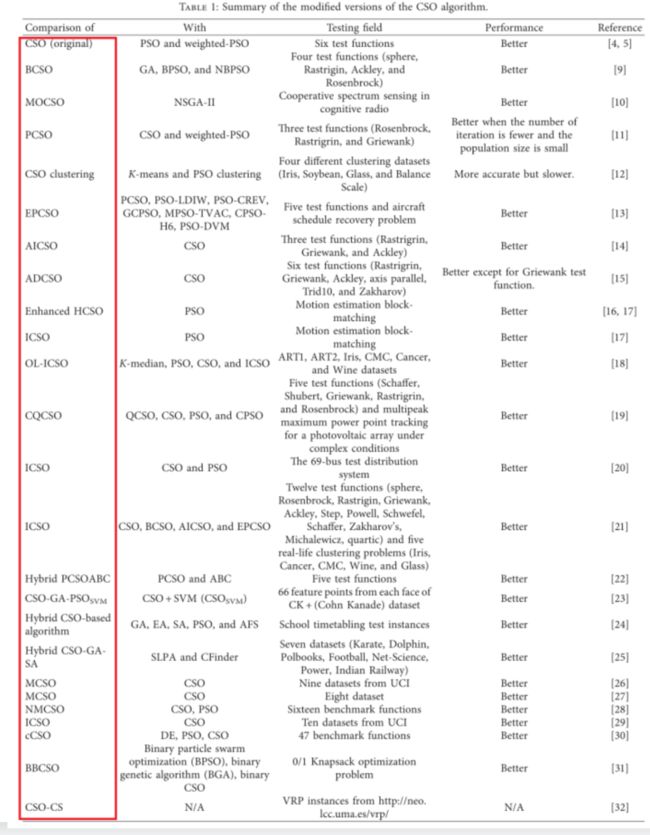
5. 算法相关改进
- 算法的二进制或多目标版本
- 改变参数
- 改变步骤
- 修改算法的结构
- 并行算法研究
- 与其他算法杂交
- 对于算法本身的思想、原理、参数设置以及种群多样性的研究,仍停留在实验探索阶段,并未有更深入的分析与讨论。关于算法收敛性的分析与证明的研究还未出现。对猫群算法的改进技术主要集中于常态的增加参数、加入部分操作算子等方面,对于算法框架、迭代进化方式等的改进的研究较少。
A. M. Ahmed, T. A. Rashid, and S. A. M. Saeed, “Cat Swarm Optimization Algorithm: A Survey and Performance Evaluation,” Computational Intelligence and Neuroscience, vol. 2020, Jan. 2020.
References
[2] 智能优化算法:猫群优化算法-附代码