代码随想录算法训练营第五十六天|583.两个字符串的删除操作、72.编辑距离
day56 2023/03/28
一、两个字符串的删除操作
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
示例:
- 输入: "sea", "eat"
- 输出: 2
- 解释: 第一步将"sea"变为"ea",第二步将"eat"变为"ea"
分析如下:
这次是两个字符串可以相互删了,这种题目也知道用动态规划的思路来解,动规五部曲,分析如下:
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
这里dp数组的定义有点点绕,大家要撸清思路。
2.确定递推公式
- 当word1[i - 1] 与 word2[j - 1]相同的时候
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
这里可能不少录友有点迷糊,从字面上理解 就是 当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么我在删 word1[i - 1],是不是就达到两个元素都删除的效果,即 dp[i][j-1] + 1。
3.dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
4.确定遍历顺序
从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
5.举例推导dp数组
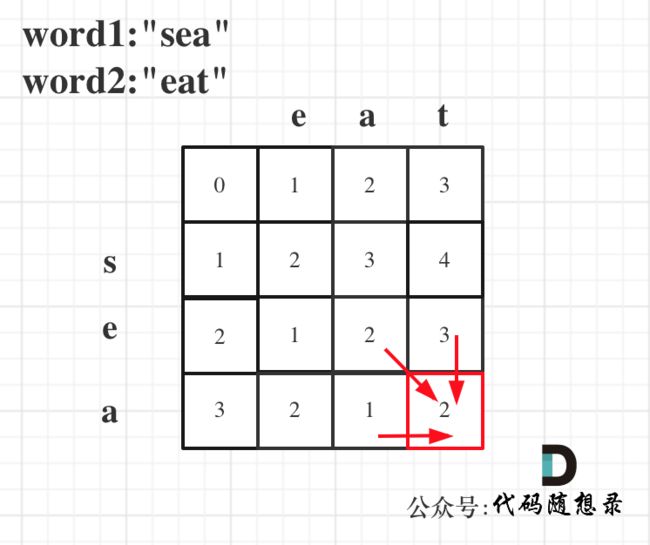
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
代码如下:
class Solution {
public:
int minDistance(string word1, string word2) {
vector> dp(word1.size() + 1, vector(word2.size() + 1));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
}
}
}
return dp[word1.size()][word2.size()];
}
}; 二、编辑距离
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
-
插入一个字符
-
删除一个字符
-
替换一个字符
-
示例 1:
-
输入:word1 = "horse", word2 = "ros"
-
输出:3
-
解释: horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
-
示例 2:
-
输入:word1 = "intention", word2 = "execution"
-
输出:5
-
解释: intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')
分析如下:
1.确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
2. 确定递推公式
if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
此时可能有同学有点不明白,为啥要即dp[i][j] = dp[i - 1][j - 1]呢?
那么就在回顾上面讲过的dp[i][j]的定义,word1[i - 1] 与 word2[j - 1]相等了,那么就不用编辑了,以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是 dp[i][j]了。
在下面的讲解中,如果哪里看不懂,就回想一下dp[i][j]的定义,就明白了。
在整个动规的过程中,最为关键就是正确理解dp[i][j]的定义!
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
- 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
- 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
可以回顾一下,if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
3. dp数组如何初始化
再回顾一下dp[i][j]的定义:
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
那么dp[i][0] 和 dp[0][j] 表示什么呢?
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;
同理dp[0][j] = j;
4. 确定遍历顺序
从如下四个递推公式:
dp[i][j] = dp[i - 1][j - 1]dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j] = dp[i][j - 1] + 1dp[i][j] = dp[i - 1][j] + 1
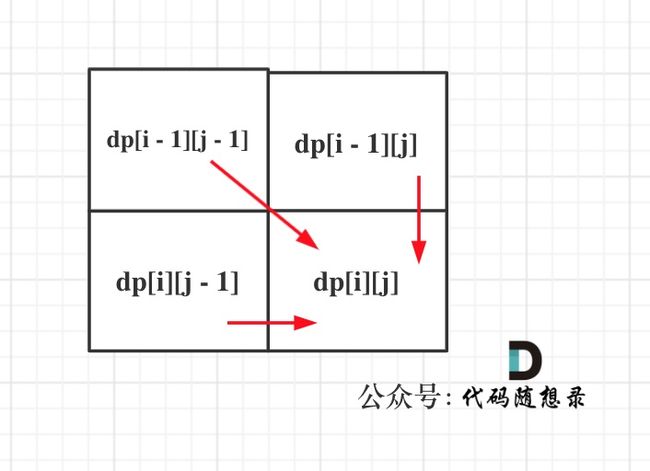
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:
所以在dp矩阵中一定是从左到右从上到下去遍历。
5.举例推导dp数组
代码如下:
class Solution {
public:
int minDistance(string word1, string word2) {
vector> dp(word1.size() + 1, vector(word2.size() + 1, 0));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
}
else {
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
}
}
return dp[word1.size()][word2.size()];
}
}; 复习一下之前的dp(温故而知新嘛)
组合总和Ⅳ:
注意:求组合数就是外层for遍历物品,内层for遍历背包
求排列数就是外层for遍历背包,内层for遍历物品
代码如下:
#include
using namespace std;
int target;
vector nums;
int main()
{
scanf("%d",&target);
int x;
while(scanf("%d",&x)!=EOF) nums.push_back(x);
vector dp(target+1,0);//初始化dp数组
dp[0]=1;
for(int i=0;i<=target;i++)
{
for(int j=0;j=nums[j])
dp[i]+=dp[i-nums[j]];
}
printf("%d\n",dp[target]);
return 0;
} 爬楼梯相当于完全背包问题呢(将m赋值为2即可得到爬楼梯题目可以AC的题解)
//爬楼梯问题进阶
#include
using namespace std;
int n,m;
int main()
{
scanf("%d%d",&n,&m);
//n表示要爬的楼梯数(相当于背包)
//m表示每次最多可以爬的楼梯数(相当于物品)
vector dp(n+1,0);
dp[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
if(i-j>=0)
dp[i]+=dp[i-j];
}
printf("%d\n",dp[n]);
return 0;
} 零钱兑换
#include
using namespace std;
int amount;
vector coins;
int main()
{
scanf("%d",&amount);
int x;
while(scanf("%d",&x)!=EOF) coins.push_back(x);
vector dp(amount+1,INT_MAX);
dp[0]=0;//初始化dp数组
for(int i=0;i 完全平方数代码如下:(完全背包)
#include
using namespace std;
int n;
int main()
{
scanf("%d",&n);
int x;
//dp[i]表示和为i的完全平方数的最少数量
//n代表背包
//每个完全平方数代表物品
vector dp(n+1,INT_MAX);
dp[0]=0;
for(int i=1;i*i<=n;i++)//遍历物品
{
for(int j=1;j<=n;j++)//遍历背包
{
if(j>=i*i)
dp[j]=min(dp[j],dp[j-i*i]+1);
}
}
if(dp[n]!=INT_MAX)
printf("%d\n",dp[n]);
else printf("-1\n");
return 0;
} 单词拆分(完全背包)
#include
using namespace std;
string s;
set wordSet;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>s;
string str;
while(cin>>str) wordSet.insert(str);
//字符串s代表背包,单词代表物品
vectordp(s.size()+1,false);
dp[0]=true;
//初始化dp数组
for(int i=1;i<=s.size();i++)//遍历背包
{
for(int j=0;j 打家劫舍系列问题
Ⅰ代码如下:
//打家劫舍
#include
using namespace std;
vector nums;
int main()
{
int x;
while(scanf("%d",&x)!=EOF) nums.push_back(x);
if(nums.size()==0) printf("0\n");
if(nums.size()==1) printf("%d\n",nums[0]);
vectordp(nums.size()+1,0);
dp[0]=nums[0];
dp[1]=max(nums[0],nums[1]);
for(int i=2;i<=nums.size();i++)
dp[i]=max(dp[i-2]+nums[i],dp[i-1]);
printf("%d\n",dp[nums.size()]);
return 0;
}