神经网络之反向传播算法（均方根反向传播算法RMSProp）

均方根反向传播算法（RMSProp）

自适应梯度算法（Adaptive gradient algorithm，Adagrad）让每个参数在迭代过程中按照不同的学习率进行自适应调整，但其本身仍存在问题，由于该算法对梯度值进行不断的累积平方，因此无论数据特征如何，在达到一定的迭代次数后，累积平方会累加到一个较大值，此时计算得到的学习率将会变得极小，并会导致每次参数的更新量变得极小，最后更新速度停滞，训练也会随之结束。
为解决上述问题，研究者们在该算法的基础上提出了均方根反向传播算法（Root mean square BackPropagation，RMSProp）。
自适应梯度算法（Adagrad）原理参考：
神经网络之反向传播算法（自适应梯度算法Adagrad）

1、算法原理

均方根反向传播相较于自适应梯度算法的主要改进点为对累积梯度的计算方式进行了调整，具体的计算公式如下：

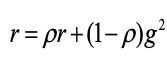
其中ρ为衰减系数。
梯度g的计算原理参考：
神经网络之反向传播算法（梯度、误差反向传播算法BP）

在对梯度平方进行累积时，主要目的在于对过去历史梯度信息的获取，而上述计算公式中衰减系数的加入则可以控制历史梯度信息获取量的多少，它相当于采用了一个变量均方根来记录历史更新次数里的梯度平方的平均值，并以此作为对学习率进行调整的主要依据。采用此方法最大的一个优点在于无论迭代多少次，参数的调整量是以历史梯度信息的平均值作为参考依据，因此其参数的更新量相对来说更加缓和，也不会出现更新速度停滞、训练提前结束的情况。
综上所述，均方根反向传播算法的算法核心思想可以视作给每一个参数设置一个均方值来计算历史梯度平方的平均值，之后再以全局学习率除以该均方值来获得此迭代次数下学习率，最后以此学习率与当下梯度值相乘获得参数的更新量。
将均方根反向传播算法应用于神经网络反向传播过程时的算法步骤如下：

1. 随机初始化神经网络中所有的参数；
2. 设置全局学习率μ、参数δ及衰减系数ρ，初始化梯度的累积平方；
3. 输入数据，按照前向传播过程计算网络的输出；
4. 使用损失函数计算误差值；
5. 根据误差值计算出隐含层、输出层每个参数的均方值；
6. 根据每个参数对应均方值、全局学习率计算其更新量；
7. 利用更新量对参数进行更新；
8. 重复步骤3到步骤7，当满足停止迭代条件时输出训练后的参数。

参数初始化方法参考：
神经网络基础知识之参数初始化

2、算法实现

以数据预测为例，下面介绍均方根反向传播算法的实现过程，将均方根反向传播算法应用于普通的三层神经网络（输入层、隐含层、输出层）的反向传播过程。
选用某省市的表层土壤重金属元素数据集作为实验数据，该数据集总共96组，随机选择其中的24组作为测试数据集，72组作为训练数据集。选取重金属Ti的含量作为待预测的输出特征，选取重金属Co、Cr、Mg、Pb作为模型的输入特征。

2.1 训练过程

#库的导入
import numpy as np
import pandas as pd

#激活函数tanh
def tanh(x):
    return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
#激活函数偏导数
def de_tanh(x):
    return (1-x**2)

#梯度累积平方计算函数，0.9为衰减系数，0.1为1-衰减系数的计算结果，输入参数r为累积梯度平方，delta为当前梯度
def accumulation(r,delta):
    r = 0.9 * r + 0.1 * (delta**2)
    return  r
#参数更新函数，w为待更新参数，r为累积梯度平方，delta为当前梯度，另外0.01为学习率
def adjust(w,r,delta):
    change1 =(0.000001+r) ** (0.5)
    change2 =delta/change1
    change = (-0.01)*change2
    w = w + change
    return w

maxepochs = 1000  #迭代训练次数
errorfinal = 0.65*10**(-3)  #停止训练误差阈值
samnum = 72  #输入数据数量
indim = 4  #输入层节点数
outdim = 1  #输出层节点数
hiddenunitnum = 8  #隐含层节点数

#输入数据的导入
df = pd.read_csv("train.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
samplein = np.mat([Co,Cr,Mg,Pb])
sampleout = np.mat([Ti])
#数据归一化，将输入数据压缩至0到1之间，便于计算，后续通过反归一化恢复原始值
sampleinminmax = np.array([samplein.min(axis=1).T.tolist()[0],samplein.max(axis=1).T.tolist()[0]]).transpose()
sampleoutminmax = np.array([sampleout.min(axis=1).T.tolist()[0],sampleout.max(axis=1).T.tolist()[0]]).transpose()
sampleinnorm = (2*(np.array(samplein.T)-sampleinminmax.transpose()[0])/(sampleinminmax.transpose()[1]-sampleinminmax.transpose()[0])-1).transpose()
sampleoutnorm = (2*(np.array(sampleout.T)-sampleoutminmax.transpose()[0])/(sampleoutminmax.transpose()[1]-sampleoutminmax.transpose()[0])-1).transpose()

sampleinmax = np.array([sampleinnorm.max(axis=1).T.tolist()]).transpose()
sampleinmin = np.array([sampleinnorm.min(axis=1).T.tolist()]).transpose()
#为归一化后的数据添加噪声
noise = 0.03*np.random.rand(sampleoutnorm.shape[0],sampleoutnorm.shape[1])
sampleoutnorm += noise
sampleinnorm = np.mat(sampleinnorm)

#利用归一化后的输入数据初始化参数w1、b1、w2、b2
dvalue = sampleinmax-sampleinmin
valuemid=(sampleinmin+sampleinmax)/2
wmag=0.7*(hiddenunitnum**(1/indim))
rand1=np.random.rand(hiddenunitnum,outdim)
rand2=np.random.randn(hiddenunitnum,indim)
rand1=rand1*wmag
rand2=rand2*wmag
b1=rand1-np.dot(rand2,valuemid)
for i in range(hiddenunitnum):
    for j in range(indim):
        rand2[i][j]=(2*rand2[i][j])/dvalue[j]
w1=rand2
w2 = np.random.uniform(low=-1, high=1, size=[outdim,hiddenunitnum])
b2 = np.random.uniform(low=-1, high=1, size=[outdim,1])

#参数w1、b1、w2、b2均为矩阵形式参与计算，其形状依次为8*4，8*1，1*8，1*1
w1 = np.mat(w1)
b1 = np.mat(b1)
w2 = np.mat(w2)
b2 = np.mat(b2)

#errhistory存储每次训练后的预测值与真实值的误差
errhistory = []

#rw1、rb1，rw2，rb2分别保存参数w1、b1、w2、b2的累积梯度，其形状与w1、b1、w2、b2一一对应
rw1 = np.zeros((8,4))
rb1 = np.zeros((8,1))
rw2 = np.zeros((1,8))
rb2 = np.zeros((1,1))

for i in range(maxepochs):
    #前向传播
    #计算隐含层输出hiddenout，输出层输出networkout
    hiddenout = tanh((np.dot(w1,sampleinnorm).transpose()+b1.transpose())).transpose()
    networkout = np.dot(w2,hiddenout).transpose()+b2.transpose()
    for j in range(samnum):
        networkout[j,:] = tanh(networkout[j,:])
    networkout = networkout.transpose()
    #计算损失函数
    err = sampleoutnorm - networkout
    loss = np.sum(np.abs(err))/samnum
    sse = np.sum(np.square(err))
    #判断是否满足停止训练条件
    errhistory.append(sse)
    if sse < errorfinal:
        break
    #反向传播
    #利用损失函数计算结果和激活函数偏导数，来计算参数w1、b1、w2、b2的梯度值
    delta2 = np.zeros((outdim,samnum))
    for n in range(samnum):
        delta2[:,n] = (-1) * err[:,n] * de_tanh(networkout[:,n])
    delta1 = np.zeros((hiddenunitnum,samnum))
    for e in range(samnum):
        for f in range(hiddenunitnum):
            delta1[f,e] = w2[:,f] * delta2[:,e] * de_tanh(hiddenout[f,e])
    dw2now = np.dot(delta2,hiddenout.transpose()) #1*8
    db2now = np.dot(delta2,np.ones((samnum,1))) #1*1
    dw1now = np.dot(delta1,sampleinnorm.transpose()) #8*4
    db1now = np.dot(delta1,np.ones((samnum,1))) #8*1

    #先更新输出层参数
    #w2更新，依次更新w2的梯度累积平方、w2
    for m in range(hiddenunitnum):
        rw2[:,m] = accumulation(rw2[:,m],dw2now[:,m])
        w2[:,m]= adjust(w2[:,m],rw2[:,m],dw2now[:,m])

    #b2更新，依次更新b2的梯度累积平方、b2
    rb2 = accumulation(rb2,db2now)
    b2 = adjust(b2,rb2,db2now)

    #更新隐含层参数
    #w1更新，依次更新w1的梯度累积平方、w1
    for a in range(hiddenunitnum):
        for b in range(indim):
            rw1[a,b] = accumulation(rw1[a,b],dw1now[a,b])
            w1[a,b] = adjust(w1[a,b],rw1[a,b],dw1now[a,b])

    #b1更新，依次更新b1的梯度累积平方、b1
    for n in range(hiddenunitnum):
        rb1[n,:] = accumulation(rb1[n,:],db1now[n,:])
        b1[n,:] = adjust(b1[n,:],rb1[n,:],db1now[n,:])
    print("the generation is:",i,",the loss is:",loss)

#达到最大训练次数，保存此时的参数w1、b1、w2、b2
np.save("w1.npy",w1)
np.save("b1.npy",b1)
np.save("w2.npy",w2)
np.save("b2.npy",b2)

2.2 测试过程及结果

测试过程只需要利用训练过程生成的相关参数，对测试数据执行一次前向传播过程来获得预测值，之后可使用相关的误差指标对预测值进行评价，详细的测试过程源码见参考源码及数据集。

注：由于每次初始化生成的参数不同，因此对参数设置相同的神经网络进行多次训练和预测，测试结果不会完全一致，此外测试结果的好坏也会受到隐含层节点数、学习率、训练次数等参数的影响。

3、参考源码及数据集

参考源码及数据集