《Unity Shader入门精要》自学笔记（二）矩阵、空间以及获取变换矩阵思路的总结

学习目标
了解空间变换时获得新坐标的思路，尽量不深究矩阵的运算

矩阵的基础知识

矩阵是什么

线性代数的本质 - 03 - 矩阵与线性变换（真的没有偷懒）
 

正交矩阵

作用

这是个很有诱惑力的矩阵，因为如果一个矩阵被证明是正交矩阵，那就等价于：
$M^T$$M$ = $I$，$M$$M^T$ = $I$，$M^{-1}$ = $M^T$

 

判断

主要有两种方法判断：

1. 构成矩阵的向量是一组标准正交基（即组成某个坐标系的三个轴的归一化向量）
2. 矩阵只进行了旋转操作

条件太苛刻了，妥协一下：若矩阵是只进行了旋转、统一缩放，那么它需要在等式中乘上$k$或$\frac{1}{k}$

 

 

变换矩阵

基本变换矩阵

平移矩阵

$T_{}$ = $\left[\begin{array}{cccc}1& 0& 0& Tx\\ 0& 1& 0& Ty\\ 0& 0& 1& Tz\\ 0& 0& 0& 1\end{array}\right]$
 

缩放矩阵

$S_{}$ = $\left[\begin{array}{cccc}Sx& 0& 0& 0\\ 0& Sy& 0& 0\\ 0& 0& Sz& 0\\ 0& 0& 0& 1\end{array}\right]$
 

旋转矩阵

绕某一轴旋转 = 在其他两轴所组成的平面进行旋转
 
$R_{x(yoz)}$ = $\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\theta & -sin\theta & 0\\ 0& sin\theta & cos\theta & 0\\ 0& 0& 0& 1\end{array}\right]$
 
$R_{y(zox)}$ = $\left[\begin{array}{cccc}cos\theta & 0& sin\theta & 0\\ 0& 1& 0& 0\\ -sin\theta & 0& cos\theta & 0\\ 0& 0& 0& 1\end{array}\right]$
 
$R_{z(xoy)}$ = $\left[\begin{array}{cccc}cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$
 
$R_x$和$R_z$直接在二维旋转矩阵的基础上插入所绕轴，并用0和1替代
 
$R_y$表现出来的$sin\theta$的正负和$R_x$和$R_z$相反，可以理解为：
在$zox$平面中，并没有按照$xyz$的顺序相乘（如$xoy$、$xoz$、$yoz$），所以要在$\theta$前加一个负号，化简后得到了$sin\theta$与$R_x$、$R_z$相反的$R_y$
 
至于为啥$R_y$是$zox$不是$xoz$，可以画一个右手系的坐标系，然后用向量叉乘的右手定则比划一下就了解啦

 

Unity中的内置变换矩阵

进行下一步前先看一下Unity提供的内置变换矩阵：

既然这里又有MVP变换矩阵，还有各自分开的其他变换矩阵，就说明在Shader它们肯定是比较常用的，也就是说还需要对每一个变换之前和之后的状态有一个基本的理解，而不是把整个过程在脑中打包成一个MVP变换小黑盒。如此才能在之后的学习实践中如鱼得水

 

空间变换与空间变换矩阵

获取父坐标系或子坐标系

书中先提出了一个获取父坐标系或子坐标系的思路，这个思路线性代数的本质 - 03 - 矩阵与线性变换不谋而合，如果哪天又转不过弯了，记得回去看看

经常会看到说：将点A从一个空间变换到空间
但是看过上面的视频后肯定会更想把这句话替换为：将点A所在的空间变换成另一个空间

 

从坐标轴到$M_{c\to p}$

当一个坐标系的三个坐标轴$x$，$y$，$z$以及原点$O$已知时，就可以得到将它变换到父坐标系的变换矩阵$M_{c\to p}$：$\left[\begin{array}{cccc}{x}_x& y_x& z_x& o_x\\ x_y& y_y& z_y& o_y\\ x_z& y_z& z_z& o_z\\ 0& 0& 0& 1\end{array}\right]$

一列一列看就会发现这个矩阵其实完完全全就是一个从左至右摆放着3个坐标轴向量、一个原点坐标的透明小盒子罢了

 

更简化的$M_{c\to p}$

因为对于没有“位置”概念的向量（即平移向量不会做出任何改变）来说，原点$O$的坐标（平移变换）知不知道无所谓，所以上面的变换矩阵可以简化为：

$M_{c\to p}$ = $\left[\begin{array}{ccc}{x}_x& y_x& z_x\\ x_y& y_y& z_y\\ x_z& y_z& z_z\end{array}\right]$

这也是为什么Shader中会有很多截取变换矩阵的前3行前3列来对法线方向、光照方向来进行空间变换的操作

 

从$M_{c\to p}$到$M_{p\to c}$

根据逆矩阵的定义以及$M_{}$$M_{}^{-1}$ = $I_{}$，$M_{p\to c}$已经可以求出了
这里再看$M_{c\to p}$其实符合正交矩阵判断中的由标准正交基组成一条，因此可以直接使用$M_{p\to c}$ = $M_{c\to p}^T$轻松得到$M_{p\to c}$ = $\left[\begin{array}{ccc}{x}_x& x_y& x_z\\ y_x& y_y& y_z\\ z_x& z_y& z_z\end{array}\right]$

 

从$M_{p\to c}$到坐标轴

根据第一步的原理，可由$M_{p\to c}$获得父坐标系在子坐标系中的表示：$x$ = $\left[\begin{array}{c}{x}_x\\ y_x\\ z_x\end{array}\right]$，$y$ = $\left[\begin{array}{c}{x}_y\\ y_y\\ z_y\end{array}\right]$，$z$ = $\left[\begin{array}{c}{x}_z\\ y_z\\ z_z\end{array}\right]$

 

模型变换：模型空间 → 世界空间

任务：将经过旋转、缩放、平移等变换的模型的顶点坐标转换到世界坐标系

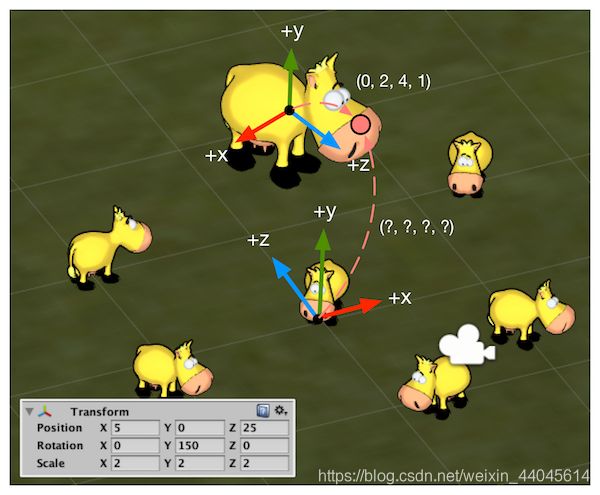
根据先缩放，再旋转，后平移的原则以及矩阵乘法的结合性，可以轻松获得模型变换矩阵
$M_{model}$ = $M_{translate}$$M_{rotate}$$M_{scale}$

 

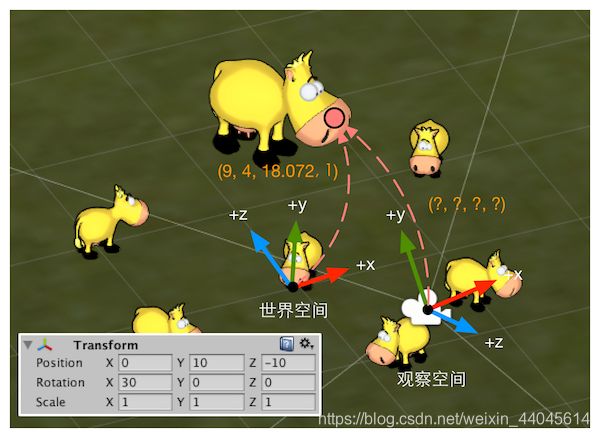
观察变换：世界空间 → 观察空间（相机的模型空间）

任务：从世界空间变换到观察空间

首先需要注意一点：Unity在观察空间中使用的是右手系，在其他空间（模型、世界、裁剪、屏幕）使用的是左手系，这也是摄像机的观察方向是-z的原因

这个从左手系到右手系的变换在一般情况下不会对Unity中的shader变成造成影响，因为Unity会做很多渲染的底层工作，其中就包括了很多坐标空间的转换

但是，如果需要调用类似Camera.cameraToWorldMatrix、Camera.worldToCameraMatrix等接口自行计算某模型在观察空间中的位置，就要注意这个差异

计算观察变换矩阵有两种思路：

1. 由相机的Transform属性得到它3个坐标轴在世界空间中的表示，然后根据前面的方法得出观察变换矩阵
2. 将相机的坐标原点移动到世界坐标系原点，再将相机的坐标轴旋转到与世界坐标系坐标轴一一重合，即通过$M_{view}$ = $M_{rotate}$$M_{translate}$得到观察变换矩阵

最后要记得乘个$S_z$ = -1的矩阵缩放矩阵来给$z$分量取个反

 

投影变换：观察空间 → 齐次裁剪空间

投影变换这个名字非常有迷惑属性，它并没有真正意义上进行投影，而是通过缩放xyz并改变w的值来到齐次裁剪空间，为投影做准备

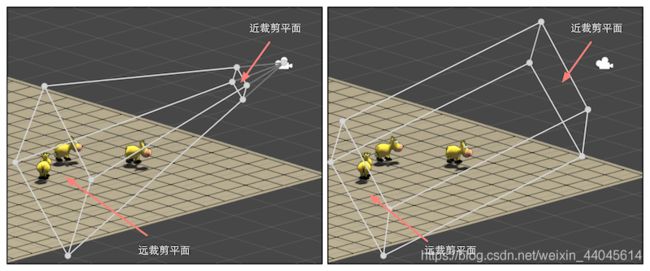
投影分为两种：透视投影（左图）和正交投影（右图）

1. 透视投影

由上图可知，决定透视投影变换矩阵的有4个变量：Near，Far，Field of View，Aspect（相机宽高比，与FOV联动间接决定了左右视角范围）

经过一系列的推导（具体可回顾GAMES101-现代计算机图形学入门-闫令琪-Lecture 04 Transformation Cont.）得到：

$M_{persp}$：$\left[\begin{array}{cccc}\frac{cot\frac{FOV}{2}}{Aspect}& 0& 0& 0\\ 0& cot\frac{FOV}{2}& 0& 0\\ 0& 0& -\frac{Far+Near}{Far-Near}& -\frac{2\cdot Far\cdot Near}{Far-Near}\\ 0& 0& -1& 0\end{array}\right]$

注意：该矩阵仅针对Unity（右手系的观察空间，矩阵左乘，变换后z分量范围在[-w，w]之间）

从变换矩阵可以看出，透视投影矩阵本质上是对$x$，$y$，$z$分量做了不同程度的缩放，并且给$z$分量做了平移

同时也可以看出，变换后的顶点$w$分量变成了-$z$

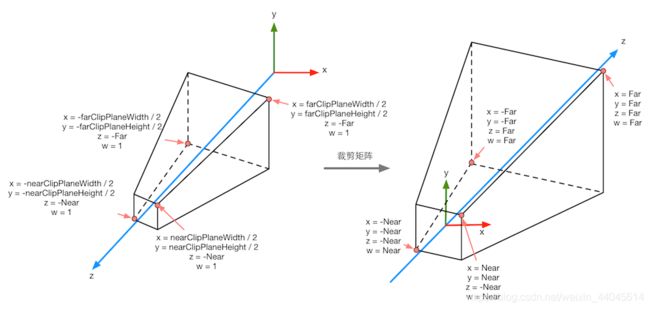
接下来就可以判断变换后的顶点是否在视锥体内了：
若在，则必须同时满足：-$w$≤-$x$≤$w$，-$w$≤-$y$≤$w$，-$w$≤-$z$≤$w$
 

 

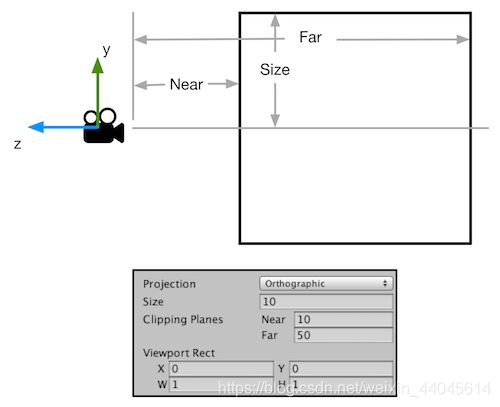
2. 正交投影

由上图可知，决定正交投影矩阵的有3个变量：Near，Far，Size，Aspect（与Size联动，间接决定横向视野范围）

经过一系列的推导（具体可回顾GAMES101-现代计算机图形学入门-闫令琪-Lecture 04 Transformation Cont.）得到：

$M_{ortho}$：$\left[\begin{array}{cccc}\frac{1}{Aspect\cdot Size}& 0& 0& 0\\ 0& \frac{1}{Size}& 0& 0\\ 0& 0& -\frac{2}{Far-Near}& -\frac{Far+Near}{Far-Near}\\ 0& 0& 0& 1\end{array}\right]$

从变换矩阵可以看出，正交矩阵本质上也是对$x$，$y$，$z$分量做了不同程度的缩放，给$z$分量做了平移

不同的是，正交投影矩阵没有改变$w$的值，依然为1

接下来就可以判断变换后的顶点是否在长方体的视锥体内了：
若在，则必须同时满足：-$w$≤-$x$≤$w$，-$w$≤-$y$≤$w$，-$w$≤-$z$≤$w$

 

屏幕映射：齐次裁剪空间 → 屏幕空间

任务：从裁剪空间变换到屏幕空间（这一步其实是Unity来做的）

第一步：齐次除法（homogeneous division，也被称为透视除法）

简单来讲就是用齐次坐标的$w$分量除以$x$，$y$，$z$分量
这一步的处理会将坐标变换到归一化的设备坐标（Normalized Device Coordinate），空间会变成一个立方体

经过透视投影和齐次除法后进入NDC：

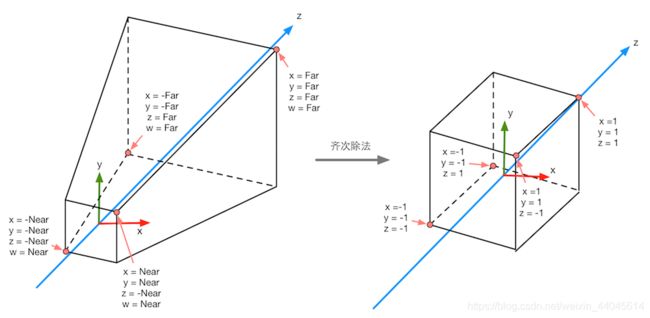
齐次除法将透视投影得到的空间再次缩放，在这里只有近平面上的点和远平面上的中心点的$x$，$y$，$z$不会被影响

经过正交投影和齐次除法后进入NDC：

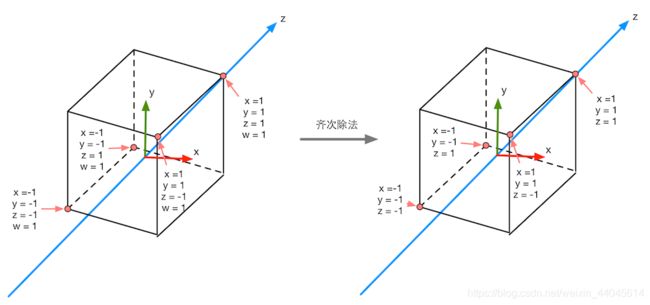
由于进行齐次除法前，正交投影产生的空间已经是一个立方体空间了，所以齐次除法并不会对顶点的$x$，$y$，$z$坐标产生影响

Unity在这里采用的是OPenGL的方式，将$x$，$y$，$z$分量的范围限定在[-1，1]
在DirectX中，$z$分量的范围是[0，1]，如果用到需要注意

 

第二步：获取屏幕空间坐标

这一步就是真正的“投影”了：将三维空间中的顶点转换到二维屏幕窗口中

Unity的屏幕坐标采用左边的标准，左下角坐标为（0，0），右上角坐标为（pixelWidth，pixelHeight）
接下来就是将当前的2 × 2方形平面缩放成pixelWidth × pixelHeight屏幕大小的矩形空间

PS：关于像素Pixel

“像素”像素可以理解为组成图像的基本元素，是一个“不可细分”方形的区域（颜色上不可细分，在反走样的采样上可以细分），它需要与“图素”区分开

一个像素的坐标就是这个像素的中点所在位置

 

最终的屏幕坐标

将上面两步总结一下，就可以得出经过齐次除法和屏幕映射得到的屏幕坐标:

$scree{n}_x$ = $\frac{cli{p}_x\cdot pixelWidth}{2\cdot cli{p}_w}$ + $\frac{pixelWidth}{2}$
$scree{n}_y$ = $\frac{cli{p}_y\cdot pixelHeight}{2\cdot cli{p}_w}$ + $\frac{pixelHeight}{2}$

上面的式子对xy分量做了缩放平移处理，z和w分量也会被以其他方式存储起来，以便将来使用

如z分量将会被用于深度缓冲，w分量将会被用于透视矫正插值等

一个传统的做法（非必须，还有其他方法）是将它们使用$\frac{cli{p}_z}{cli{p}_w}$存储起来

空间变换总结

看着图写一遍还记着的要点咯，看看还记得多少

 

法线变换与切线空间

法线与切线

法线Normal是垂直于当前点、线、面的向量，它可以在片元着色器中帮助计算光照等操作
切线Tangent是两顶点坐标相减获得的向量，它可以和BiTangent、Normal一起构成切线空间
切线空间中，Tangent轴和BiTangent轴分别于纹理空间中的u、v对齐，Normal轴垂直于它们组成的平面

 

与变换矩阵相乘后的法线与切线

由于切线本身就是两顶点相减得到的，可以直接将切线与变换矩阵相乘，来得到变换后的切线
但法线是由垂直约束得到的，直接将法线与变换矩阵相乘就有可能无法得到正确的变换后的法线，如下图

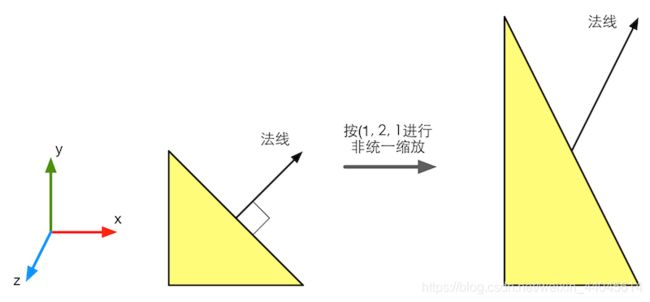
这个可以在线性代数的本质 - 03 - 矩阵与线性变换这系列视频中清楚的理解，在一些非统一缩放（视频中的两坐标轴不同比例拉伸）中，相互垂直的网格线全部变成了非垂直

 

法线变换矩阵的获取

切线的变换矩阵$M_{A\to B}$已知，可以得到：① 变换后的切线$T_B$ = $M_{A\to B}$$T_A$

设法线变换矩阵为$G_{A\to B}$，则有： ② $N_B$ = $G_{A\to B}$$N_A$

变换后的切线和法线依然满足互相垂直：③ $T_B$·$N_B$ = $0$

下面的推导理解上可能有点绕，需要记得 $T_B$和$N_B$既可以当做向量，又可以当做列矩阵

将③从向量点积转换成矩阵乘法，这就需要通过转置来让两个矩阵的行列数符合矩阵乘法的前提条件：将$T_B$进行转置后得到行矩阵$T_B^T$，再用它乘以列矩阵$N_B$，得到：

④ $T_B^T$$N_B$ = $0$

接着将①②代入④中，得到：

⑤ $($$M_{A\to B}$ $T_A$)${}^T$ ($G_{A\to B}$$N_A$) = $0$

将括号打开，得到：

⑥ $T_A^T$$M_{A\to B}^T$ $G_{A\to B}$$N_A$ = $0$

这时想起来还有一个⑦：$T_A$·$N_A$ = $0$，同样转换成矩阵乘法后获得⑧ $T_A^T$·$N_A$ = $0$

于是⑧和⑥相视一笑，⑥终于找到了藏在自家内部伪装成$M_{A\to B}^T$$G_{A\to B}$的单位矩阵$I$：

⑩ $M_{A\to B}^T$ $G_{A\to B}$ = $I$

要想等式成立，让$M_{A\to B}^T$和$G_{A\to B}$互为逆矩阵就好了

即：$G_{A\to B}$ = ($M_{A\to B}^T{)}^{-1}$ = ($M_{A\to B}^{-1}{)}^T$，也就是原变换矩阵的逆转置矩阵

 

如果…$M_{A\to B}$是一个正交矩阵？

那么$M_{A\to B}^{-1}$ = $M_{A\to B}^T$，直接 ($M_{A\to B}^T{)}^{-1}$ = $M_{A\to B}$

也就是说，如果变换质保函旋转和统一缩放，就可以利用统一缩放系数k来得到变换矩阵$M_{A\to B}$的逆转置矩阵 ($M_{A\to B}^T{)}^{-1}$ = $\frac{1}{k}$$M_{A\to B}$
否则，就要老老实实去求解逆转置矩阵了

 

 

参考资料
Unity Shader入门精要-冯乐乐
GAMES101-现代计算机图形学入门-闫令琪
切线空间（Tangent Space）完全解析