蓝桥杯第一次训练赛题解

蓝桥杯第一次训练赛题解

A+B for Input-Output Practice (I)

题目描述

Description
计算A+B
程序设计任务中常常会包含多组输入输出。
Input
第一行一个正整数n，代表输入数据的组数。
以下n行，每行两个正整数
Output
计算这n组数的和，每组答案占一行
Sample Input
2
1 5
10 20
Sample Output
6
30

代码

#include 
using namespace std;
int n, a, b;

int main() {
	scanf("%d", &n);
	while (n--) { //for(int i=1;i<=n;++i)
		scanf("%d%d", &a, &b);
		printf("%d\n", a + b);
	}
	return 0;
}

复读机 for Input-Output Practice (V)

题目描述

Description
所谓复读机，那就是复读，就是复读，就是复读，就是复读…
Input
第一行包括一个正整数T，表示输入数据组数。(1 < T < 10)

每一组输入数据为长度不超过20的一句话。

Output
对于每组输入，原样输出输入的内容。
Sample Input

3
Hello World!
I love NCST!
I love ACM!

Sample Output

Hello World!
I love NCST!
I love ACM!

题目讲解

scanf语句在接收字符串的时候遇到空格和回车会自动结束并且空格和回车还遗留在缓冲区内。但是使用%[]可以用来进行多个字符的输入,并对结束符进行自定义。例如

scanf("%[^\n]",src);//直到输入回车键，读取才结束，当然不能超过a定义的大小，否则会出错。

当然这种方法并不常用。
gets()语句遇到空格不停止，遇到回车停止。
也可以使用getline(cin,s)这样的方式接收字符串。

代码

#include 
using namespace std;
int T;
char s[200];
string ss;

int main() {
	scanf("%d", &T);
	getchar();
	while (T--) { //for(int i=1;i<=n;++i)
		//	cin.getline(s, 20);
//		cout << s << endl;
		getline(cin, ss);
		cout << ss << endl;
	}
	return 0;
}/*
cin>>s;//scanf("%s",s);
X
*/

[蓝桥杯][算法提高]删除数组中的0元素

题目描述

Description
编写函数CompactIntegers，删除数组中所有值为0的元素，其后元素向数组首端移动。

注意，CompactIntegers函数需要接收数组及其元素个数作为参数，函数返回值应为删除操作执行后数组的新元素个数。

输入时首先读入数组长度，再依次读入每个元素。
将调用此函数后得到的数组和函数返回值输出。
Input
Output
Sample Input
7
2 0 4 3 0 0 5
Sample Output
2 4 3 5
4

题目讲解

题目要求删除那些值为0的数，最简单的方法就是这样接收字符串边判断是否满足输出条件。并使用一个变量记录有效的输出个数。

代码

#include 
using namespace std;
int n, a[100], p;

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
		scanf("%d", &a[i]);
	for (int i = 1; i <= n; ++i) {
		if (a[i] != 0) {
			printf("%d ", a[i]);
			p++;
		}
	}
	cout << endl;
	printf("%d", p);
	return 0;
}/*

*/

[蓝桥杯][算法训练]斜率计算

题目描述

Description
输入两个点的坐标，即p1 = (x1, y1)和p2=(x2, y2)，求过这两个点的直线的斜率。如果斜率为无穷大输出“INF”。
Input
输入包含多组数据，每组数据之间用空行分开

每组数据有两行

第一行为 x1 y1

第二行为 x2 y2

Output
按顺序输出每组数据的结果，以空行做分隔，结果保留两位小数

Sample Input
1 2
2 4

1 2
1 4

1 2
3 2

Sample Output
2.00

INF

0.00

题目讲解

这个题目并没有指明有多少组输入。所以我们使用while循环，循环的截止条件就使用scanf的返回值判断有无输入。有以下几种形式。

while(~scanf("%lf%lf\n%lf%lf",&x1,&y1,&x2,&y2))
while(scanf("%lf %lf %lf %lf",&x_1,&y_1,&x_2,&y_2)!=EOF)

代码

#include 
using namespace std;
double X1, X2, Y1, Y2;

int main() {
	while (scanf("%lf%lf%lf%lf", &X1, &Y1, &X2, &Y2) != EOF) {
		if (fabs(X1 - X2) == 0)
			printf("INF\n\n");
		else
			printf("%.2lf\n\n", (Y2 - Y1) / (X2 - X1));
	}
	return 0;
}/*

*/

[PAT乙级]害死人不偿命的(3n+1)猜想

题目描述

Description

卡拉兹(Callatz)猜想：
对任何一个自然数n，如果它是偶数，那么把它砍掉一半（n=n/2）；如果它是奇数，那么把3n+1砍掉一半(n=(3*n+1)/2)。这样一直反复砍下去，最后一定在某一步得到n=1。卡拉兹在1950年的世界数学家大会上公布了这个猜想，传说当时耶鲁大学师生齐动员，拼命想证明这个貌似很傻很天真的命题，结果闹得学生们无心学业，一心只证(3n+1)，以至于有人说这是一个阴谋，卡拉兹是在蓄意延缓美国数学界教学与科研的进展……
我们今天的题目不是证明卡拉兹猜想，而是对给定的任一不超过1000的正整数n，简单地数一下，需要多少步（砍几下）才能得到n=1？

Input

每个测试输入包含1个测试用例，即给出自然数n的值。

Output

输出从n计算到1需要的步数。

Sample Input
3
Sample Output
5

题目讲解

这道题十分的简单直接模拟就好。

代码

#include 
using namespace std;
int n, ans;

int main() {
	scanf("%d", &n);
	while (n != 1) {
		if (n % 2 == 0)
			n = n / 2;
		else
			n = (3 * n + 1) / 2;
		ans++;
	}
	printf("%d", ans);
	return 0;
}/*

*/

D进制的A+B

题目描述

Description

输入两个非负10进制整数A和B(≤2^30-1)，输出A+B的D (1 < D <= 10)进制数。

Input

A B D

Output

输出A+B的D (1 < D <= 10)进制数。

Sample Input
2 4 2
Sample Output
110

题目讲解

本题一知两个十进制的数A，B并且这两个数都小于2³⁰-1大家都知道通常int的范围是负2³⁰-1道2³⁰-1但是保险起见我们可以使用long long 存储这次的数据。根据十进制转化为D进制的方法：

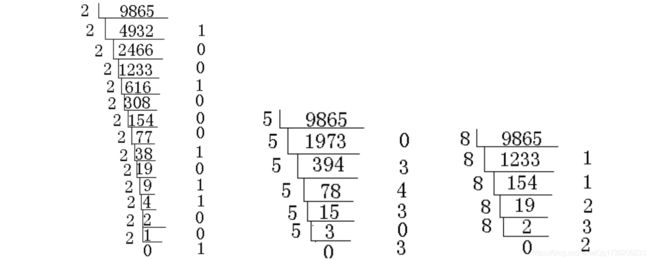
上图为对9865求2进制，5进制和8进制
二进制：10011010001001
五进制：303430
八进制：23211
通过这个图片相信大家已经明白如何计算，就是9865对D取余，余数构成D进制各位数值，之后再用9865除D取整一直计算道除D后为零。以下是代码

代码

#include 
using namespace std;
int A, B, D;
int a[100], n;

int main() {
	scanf("%d%d%d", &A, &B, &D);
	A = A + B;
	while (A) {
		n++;
		a[n] = A % D;
		A = A / D;
	}
	for (int i = n; i >= 1; --i)
		printf("%d", a[i]);
	return 0;
}/*

*/

[算法竞赛进阶指南]A^B

题目描述

Description

求a的b次方对p取模的值，其中 0 ≤ a,b,p ≤ 109

Input

a,b,p

Output

输出a的b次方对p取模的值

Sample Input
123478623 0 1000000000
Sample Output
1

题目讲解

正常来说，计算机每秒可运算10⁷-10⁸次（以c++语言来说）
所以这题如果用循环一个个的来乘，最大有10^9的运算量，有可能超时。所以这道题应采用快速幂算法
以上面提供的数据来说明 快速幂：

7转化为二进制为111
2^0=1
2^1=2
2^2=4
2^3=8
……

3⁷=3¹¹¹(111为二进制状态)
3⁷=3¹*3²*3⁴(7=1+2+4)

每一项是上一项的平方……

代码

#include 
using namespace std;
typedef long long ll;

ll quick_pow(ll a, ll n, ll z) { //a^n %z
	ll re = 1;
	while (n != 0) {
		if (n & 1) //判断n的最后一位是1还是0
			re = re  * a % z;
		a = (a * a) % z; //将a平方，即把a^(2^i)变为a^(2^(i + 1))
		n >>= 1;//n右移一位，舍去n的最后一位
	}
	return re % z;
}
ll a, b, p;

int main() {
	scanf("%lld%lld%lld", &a, &b, &p);
	cout << quick_pow(a, b, p);
	return 0;
}/*

*/