python高斯滤波器高通锐化_SciPyTutorial-图像的高斯滤波

23. Scipy Tutorial-图像的高斯滤波

高斯滤波器是一种线性滤波器，能够有效的抑制噪声，平滑图像。其作用原理和均值滤波器类似，都是取滤波器窗口内的像素的均值作为输出。其窗口模板的系数和均值滤波器不同，均值滤波器的模板系数都是相同的为1；而高斯滤波器的模板系数，则随着距离模板中心的增大而系数减小。所以，高斯滤波器相比于均值滤波器对图像个模糊程度较小。利用高斯核对一个2维图像数据进行卷积可以使得图像$blur$模糊化(去除细节和噪声)。高斯滤波后图像被平滑的程度取决于标准差$\sigma$。它的输出是领域像素的加权平均，同时离中心越近的像素权重越高。因此，相对于均值滤波（mean filter）它的平滑效果更柔和，而且边缘保留的也更好。

23.1 高斯函数

Gaussina Function的数学公式在二维空间定义为：

$$

G(x,y) =a e^{ -\frac{(x - x_0)^2}{2\sigma_1^2 } - \frac{(y - y_0)^2}{2\sigma_2^2 } }

$$

其中$(x,y)$为点坐标，在图像处理中为是整数；$\sigma$是正态分布的标准偏差, $a = \frac{1}{\sqrt{2\pi} \sigma}$。如果$x_0 = 0, y_0 = 0， \sigma_x = \sigma_y$则有：

$$

G(x,y) = ae^{ -\frac{x^2 + y ^2}{2\sigma^2 } }

$$

在实际图像处理中得到了工程人员的有效使用．高斯函数具有五个十分重要的性质，它们是：

（1）二维高斯函数具有旋转对称性，即滤波器在各个方向上的平滑程度是相同的．一般来说，一幅图像的边缘方向是事先不知道的，因此，在滤波前是无法确定一个方向上比另一方向上需要更多的平滑．旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向．

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d.axes3d import Axes3D

def g(v, std):

x = v[0]

y = v[1]

return np.exp(-((x ** 2) + (y ** 2)) / (2 * std ** 2))# * (1.0 / (2 * np.pi * std ** 2))

x = np.linspace(-25, 25, 241)

xy = np.meshgrid(x, x)

plt.figure()

ax1 = plt.subplot2grid((1,1), (0,0), projection='3d')

ax1.plot_surface(xy[0], xy[1], g(xy, 11), color = "c")

plt.show()

k = g(xy, 11)[::60, ::60]

print k, k.shape

程序执行结果：

[[0.00571141 0.03962457 0.07557387 0.03962457 0.00571141]

[0.03962457 0.27490703 0.52431577 0.27490703 0.03962457]

[0.07557387 0.52431577 1. 0.52431577 0.07557387]

[0.03962457 0.27490703 0.52431577 0.27490703 0.03962457]

[0.00571141 0.03962457 0.07557387 0.03962457 0.00571141]] (5, 5)

数据以k[2][2] = 1为中心旋转对称。有两个特点需要注意：第一就是结果里的中心位置数据最大，第二是计算结果都是小数，小数进行卷积计算有些慢，故实际图像卷积过程中常按照高斯函数的旋转对称特点设计一个$n\times n$的全整数(运算速度较小数来说快些)的方形窗口(模板)，n常为奇数，中心数值最大向四周不断地减小。所以有高斯滤波器模板一说法。

（2） 高斯函数是单值函数．这表明，高斯滤波器用像素邻域的加权均值来代替该点的像素值，而每一邻域像素点权值是随该点与中心点的距离单调增减的．这一性质是很 重要的，因为边缘是一种图像局部特征，如果平滑运算对离算子中心很远的像素点仍然有很大作用，则平滑运算会使图像失真．

（3）高斯函数的付立叶变换频谱是单瓣的．这一性质是高斯函数傅里叶变换等于高斯函数本身这一事实的直接推论．图像常被不希望的高频信号所污染(噪声和细纹理)．而所希望的图像特征（如边缘），既含有低频分量，又含有高频分量．高斯函数付立叶变换的单瓣意味着平滑图像不会被不需要的高频信号所污染，同时保留了大部分所需信号．

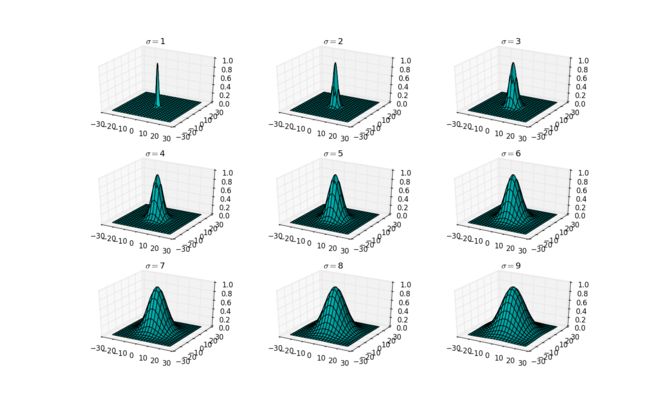
（4）高斯滤波器宽度(决定着平滑程度)是由参数σ表征的，而且σ和平滑程度的关系是非常简单的．σ越大，高斯滤波器的频带就越宽，平滑程度就越好(参考下面的程序及结果图)．通过调节平滑程度参数σ，可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(欠平滑)之间取得折衷．

#coding:utf-8

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d.axes3d import Axes3D

def g(v, std):

x = v[0]

y = v[1]

return np.exp(-((x ** 2) + (y ** 2)) / (2 * std ** 2))# * (1.0 / (2 * np.pi * std ** 2))

x = np.linspace(-25, 25, 200)

xy = np.meshgrid(x, x)

plt.figure()

for i in range(9):

print i / 3, i % 3

ax1 = plt.subplot2grid((3,3), (i / 3, i % 3), projection='3d')

ax1.plot_surface(xy[0], xy[1], g(xy, i + 1), color = "c")

s = str(i + 1)

ax1.set_title("$\sigma =$" + s)

plt.show()

$\sigma$越大，分布越分散，各部分比重差别不大，于是生成的模板各元素值差别不大，类似于平均模板；$\sigma$越小，分布越集中，中间部分所占比重远远高于其他部分，反映到高斯模板上就是中心元素值远远大于其他元素值，于是自然而然就相当于中间值得点运算。

（5）由于高斯函数的可分离性，大高斯滤波器可以得以有效地实现．二维高斯函数卷积可以分两步来进行，首先将图像与一维高斯函数进行卷积，然后将卷积结果与方向垂直的相同一维高斯函数卷积．因此，二维高斯滤波的计算量随滤波模板宽度成线性增长而不是成平方增长．

23.2 高斯(核)函数滤波

滤波是将信号中特定波段频率滤除的操作，是抑制和防止干扰的一项重要措施。是根据观察某一随机过程的结果，对另一与之有关的随机过程进行估计的概率理论与方法。图像滤波，即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制，是图像预处理中不可缺少的操作，其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。图像里色彩剧烈变化的地方，就是图像的高频区域；图像里色彩稳定平滑的地方，就是低频区域。故图像的滤波器有分为平滑空间滤波器和锐化空间滤波器。低通滤波，使得图像的高频区域变成低频，即色彩变化剧烈的区域或噪点变得平滑(消除噪点)，也就是出现模糊效果。而高通滤波，过滤了低频，只保留那些变化最快速最剧烈的区域，也就是图像里面的物体边缘，所以常用于边缘识别。

图像滤波是将二维原图像素矩阵和滤波器矩阵的对应元素的乘积求和的值作为新生成(滤波后)图像当前中心像素位置的值，这样就完成了滤波的过程了，而图像的卷积则是要对上边提及的滤波器矩阵先旋转180$^\circ$后做相同的操作。

高斯滤波器是一种线性滤波器，能够有效的抑制噪声，平滑图像。其作用原理和均值滤波器类似，都是取滤波器窗口内的像素的均值作为输出。其窗口模板的系数和均值滤波器不同，均值滤波器的模板系数都是相同的为1；而高斯滤波器的模板系数，则随着距离模板中心的增大而系数减小。所以，高斯滤波器相比于均值滤波器对图像个模糊程度较小。

在scipy里如果图像的滤波函数$w[n,m]$满足：

$$

w[n,m] = w_1[n]w_2[m]

$$

那么可以使用sepfir2d函数来实现高斯函数滤波：

$$

w[n,m] \propto e^{\frac{-(x^2 + y^2)}{2\sigma^2}} = e^{\frac{-x^2 }{2\sigma^2}}e^{\frac{-y^2 }{2\sigma^2}}

$$

在scipy的signal模块里有gaussian窗口函数，可以直接创建：

$$

w[n] = e^{\frac{-n^2 }{2\sigma^2}}

$$

由于高斯核(模板)具有旋转对称性，所以图像用高斯函数滤波处理平滑、去噪可以利用卷积(卷积需要先对核180$^\circ$旋转，但高斯旋转后还是一样)来实现。

#coding:utf-8

import numpy as np

from scipy import misc, ndimage,signal

import matplotlib.pyplot as plt

import scipy

print "scipy version is:", scipy.__version__

def g(v, std):

x = v[0]

y = v[1]

return np.exp(-((x ** 2) + (y ** 2)) / (2 * std ** 2))# * (1.0 / (2 * np.pi * std ** 2))

x = np.linspace(-3, 3, 121)#61

xy = np.meshgrid(x, x)

k = g(xy, 5.0)

k = k[::20, ::20]

img = misc.lena()

img_con = signal.convolve(img, k, mode = "valid")

img_fft = signal.fftconvolve(img, k, mode = "valid")

w = signal.gaussian(7, std = 5.0)

img_sep = signal.sepfir2d(img, w, w)

plt.gray()

plt.subplot(221, title = "orginal")

plt.imshow(img)

plt.subplot(222, title = "fftconvolve")

plt.imshow(img_fft)

plt.subplot(223, title = "sepfir2d")

plt.imshow(img_sep)

plt.subplot(224, title = "convolve")

plt.imshow(img_con)

from mpl_toolkits.mplot3d.axes3d import Axes3D

plt.figure()

ax1 = plt.subplot2grid((2,2), (0,0), projection='3d')

ax1.plot_surface(xy[0], xy[1], g(xy, 5), color = "c")

plt.show()

程序执行结果：

平滑效果请注意头发和帽沿。

解释一下程序：

（1）首先需要定义了一个二维高斯函数$g$，参数是坐标v和标准差std。

def g(v, std):

x = v[0]

y = v[1]

return np.exp(-((x ** 2) + (y ** 2)) / (2 * std ** 2))# * (1.0 / (2 * np.pi * std ** 2))

x = np.linspace(-3, 3, 121)#61

xy = np.meshgrid(x, x)

k = g(xy, 5.0)

k = k[::20, ::20]

程序里的$x$为轴数据121个，变化范围从$-3\sim 3$。meshgrid函数产生三维xoy平面的坐标点集。语句k = g(xy, 5.0)里的$k$记录二维高斯函数值，而对k取切片则是得到整数坐标点的高斯函数的计算值，形成$7\times 7$的高斯模板滤波器矩阵核。

（2）img是读取的scipy自带的内部$lena$图像数据。

img = misc.lena()

img_con = signal.convolve(img, k, mode = "valid")

img_fft = signal.fftconvolve(img, k, mode = "valid")

w = signal.gaussian(7, std = 5.0)

img_sep = signal.sepfir2d(img, w, w)

由于高斯滤波器矩阵具有旋转对称性，旋转$180^{\circ}$后一样，所以对图像的滤波可以借助卷积函数来完成，这里用convolve和fftconvolve来卷积图像数据得到对图像的滤波。

（3）scipy.signal里有gaussian函数可以生成一维的高斯窗口函数，可以借助sepfir2d卷积函数完成对图像的滤波。

w = signal.gaussian(7, std = 5.0)

img_sep = signal.sepfir2d(img, w, w)

（4）图像滤波完成以后可以可视化输出结果。

plt.gray()

plt.subplot(221, title = "orginal")

plt.imshow(img)

plt.subplot(222, title = "fftconvolve")

plt.imshow(img_fft)

plt.subplot(223, title = "sepfir2d")

plt.imshow(img_sep)

plt.subplot(224, title = "convolve")

plt.imshow(img_con)

（5）下面这段代码绘制的是程序里的二维高斯函数可视化图像。

from mpl_toolkits.mplot3d.axes3d import Axes3D

plt.figure()

ax1 = plt.subplot2grid((2,2), (0,0), projection='3d')

ax1.plot_surface(xy[0], xy[1], g(xy, 5), color = "c")

plt.show()