树形DP问题C++详解

树

在学习树形dp之前我们先了解一下什么是树。树简单来说就是连通的无环图。

树的存储

保存边信息的树的模板如下：

a表示加边的起点，b表示加边的终点，c表示加边的权值

const int N = 1e4 + 10;
int end[N], worth[N];
int next[N], head[N];
int indexes = 0;
void add(int a, int b, int c) {//a表示加边的起点，b表示加边的终点，c表示加边的权值
    end[indexes] = b; 
    worth[indexes] = c;
    next[indexes] = h[a];
    head[a] = indexes++;
}

树形DP

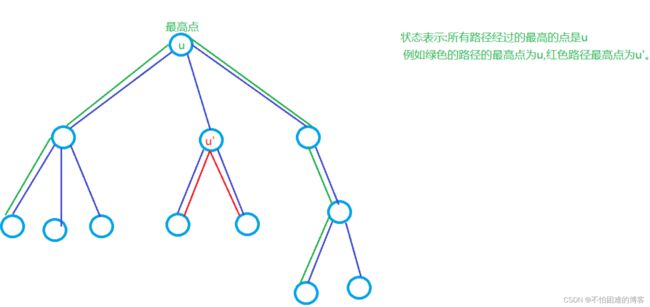
具体来说，在树形动态规划当中，我们一般先算子树再进行合并，在实现上与树的后序遍历相似，都是先遍历子树，遍历完之后将子树的值传给父亲。简单来说我们动态规划的过程大概就是先递归访问所有子树，再在根上合并。

了解了树形动态规划的基本思想后，做一些经典的树形DP题型

经典例题

1072. 树的最长路径

给定一棵树，树中包含 n个结点（编号1~n）和 n−1条无向边，每条边都有一个权值。

现在请你找到树中的一条最长路径。

换句话说，要找到一条路径，使得使得路径两端的点的距离最远。

注意：路径中可以只包含一个点。

输入格式

第一行包含整数 n。

接下来 n−1行，每行包含三个整数 ai,bi,ci，表示点 ai和 bi之间存在一条权值为 ci的边。

输出格式

输出一个整数，表示树的最长路径的长度。

数据范围

1≤n≤10000,
1≤ai,bi≤n,
−105≤ci≤105

输入样例：

6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7

输出样例：

22

思路

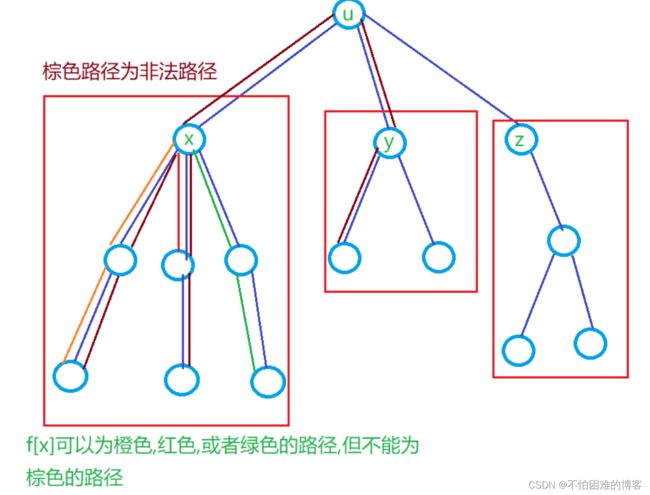
本图中f[x]表示x的子节点到x的最长距离,而非以x为顶点的最长路径.因为本题的路径是两条边,所以f[x]表示其中一条边的最大的值,f[y],f[z]同理,两条边加起来即为以u为顶点最长路径

 

注:本题的答案不一定为以u为顶点的路径,因为u到x,y,z的距离可能均为负数,所以答案可以是以x,y或者z为顶点的路径
本题采用dfs的方法来求解,所以是求解方式自下而上的

AC代码如下：

#include 
using namespace std;
const int N = 10010, M = N * 2;
int n;
int h[N], e[M], w[M], ne[M], idx;
int ans;
void add(int a, int b, int c)
{
	e[idx] = b;
	w[idx] = c;
	ne[idx] = h[a];
	h[a] = idx++;
}
int dfs(int u, int father)
{
	int dist = 0;//表示从当前点往下走的最大长度
	int d1 = 0, d2 = 0;
	for(int i = h[u]; i != -1; i = ne[i])
	{
		int j = e[i];
		if(j == father) continue;
		int d = dfs(j, u) + w[i];
		dist = max(dist, d);
		if(d >= d1) d2 = d1, d1 = d;
		else if(d > d2) d2 = d;
	}
	ans = max(ans, d1 + d2);
	return dist;
}
int main()
{
	cin >> n;
	memset(h, -1, sizeof h);
	for(int i = 0; i < n - 1; i++)
	{
		int a, b, c;
		cin >> a >> b >> c;
		add(a, b, c);
		add(b, a, c);
	}
	dfs(1, -1);
	cout << ans << endl;
	return 0;
}