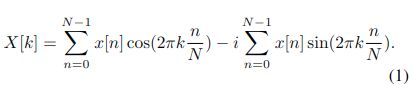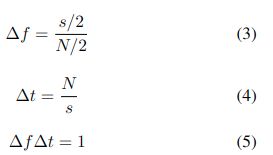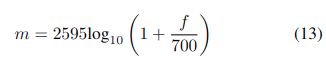nnAudio的简单介绍
官方实现
https://github.com/KinWaiCheuk/nnAudio;
论文实现:
nnAudio: An on-the-Fly GPU Audio to Spectrogram Conversion Toolbox Using 1D Convolutional Neural Networks;
以下先对文章解读:
abstract
在本文中,我们提出了nnAudio,这是一种新的基于神经网络的音频处理框架,具有图形处理单元(GPU)支持,利用1D卷积神经网络执行时域到频域转换。由于速度快,它允许实时提取光谱图,而无需在磁盘上存储任何光谱图。此外,这种方法还允许在波形到谱图转换层上进行反向传播,因此,转换过程可以进行训练,从而进一步优化神经网络所训练的特定任务的波形到谱线图转换。
所有谱线图实现都按输入长度的线性时间的Big-O缩放。然而,nnAudio利用了PyTorch的一维卷积神经网络的计算统一设备架构(CUDA),其短时傅里叶变换(STFT)、梅尔谱图和常数Q变换(CQT)实现比仅使用中央处理单元(CPU)的其他实现快了一个数量级。我们使用NVIDIA GPU在三台不同的机器上测试了我们的框架,考虑到录音长度相同,我们的框架将谱图提取时间从几秒(使用流行的python库librosa)减少到几毫秒。当将nnAudio应用于可变输入音频长度时,使用librosa从MusicNet数据集中提取具有不同参数的34种谱图类型平均需要11.5小时。nnAudio平均需要2.8小时,速度仍然是librosa的四倍。我们提出的框架在处理速度方面也优于现有的GPU处理库,如Kapre和Torchaudio。
1. introduction
自20世纪80年代以来,光谱作为音频信号的时频表示,一直被用作神经网络模型的输入[1-3]。不同类型的光谱图针对不同的应用进行定制。例如,Mel频谱图和Mel频率倒谱系数(MFCC)是为语音相关应用设计的[4,5],而常数Q变换最适合音乐相关应用[6,7]。尽管最近在音频领域的端到端学习方面取得了进展,如WaveNet[8]和SampleCNN[9],这使得对原始音频数据进行模型训练成为可能,但许多最近的出版物仍然使用声谱图作为各种应用的模型的输入[10]。这些应用包括语音识别[11,12]、语音情感检测[13]、语音到语音翻译[14]、语音增强[15]、语音分离[16]、歌声转换[17]、音乐标记[18]、覆盖检测[19]、旋律提取[20]和复调音乐转录[21]。在原始音频数据上训练端到端模型的一个缺点是训练时间较长。
本文的主要贡献是开发了一种基于GPU的音频处理框架,该框架直接集成到神经网络中并利用了神经网络的力量。这提供了以下好处:
1)使用动态时频转换层进行端到端神经网络训练(即,可以直接使用原始波形作为神经网络的输入)。
2) 与ibrosa[23]等传统音频处理方法相比,处理速度明显更快。
3) 基于可以在GPU上运行的神经网络的CQT算法(在撰写本文时,没有可以在GPU中运行的基于神经网络的CQT算法。)
4)可训练的傅立叶、梅尔和CQT内核,可以根据手头的问题自动调整。
比较(A):现有(慢速)方法[32-40]和(b):我们提出的(如图11a所示快得多)基于神经网络的音频处理框架(nnAudio)的流程图。我们提出的神经网络以黄色突出显示。我们现在可以直接将波形前馈到神经网络,而不是对波形进行预处理,并且可以在训练过程中动态生成频谱图。红色箭头表示反向传播ŞL可以走多远,这允许在训练期间对初始化的内核进行微调,从而产生专门定制的新表示。
在下面的小节中,我们将简要总结离散傅立叶变换(DFT)的数学原理。
然后,我们将讨论如何初始化神经网络来执行第II节中的STFT、Mel谱图和常数Q变换(CQT)。
在第四节中,我们比较了nnAudio与流行的python信号处理库librosa的速度和输出。最后,我们介绍了我们库的潜在应用。
2. signal processing:
在本节中,我们将介绍用于将信号从时域转换到频域的基本变换方法(DFT)。欢迎在信号处理方面有扎实背景的读者跳过本节,可以继续阅读第三节。
2.1 DFT
当使用任何计算机或移动设备录制音频时,在存储数据之前,模拟信号会转换为数字信号。因此,音频波形由离散的数据点组成。离散傅立叶变换可以用于将该离散信号从时域转换到频域。
方程(1)显示了离散傅立叶变换[41]的数学表达式,其中X[k]是频域中的输出;并且x[n]是时域中的音频输入的第n个样本。
对于实值输入,频域输出X[k], k ∈[1,N/2];
X[k]的 另一部分,k ∈[N/2, N/2 -1] 和前一部分在数值上相等,但是顺序相反, 体现在坐标轴上,两者便是构成一个对称的波形
为了丢弃该冗余频域信息,只提取频域中的前半个频率轴,即k∈[0,N/2]。我们将DFT定义为实数分量和复数分量的分解和:
其中N是窗口长度(通常是2的幂,如1024和2048)。
当我们使用(1)用一维卷积神经网络计算DFT时,我们可以使用实值算法分别计算实项和复项。
DFT中的频率k以归一化频率(相当于每个窗的周期)给出。
通过下面的公式, 将归一化频率k 转化为以 HZ为单位的频率 f f f,
f = k s N , ( 2 ) f = k \frac{s}{N}, (2) f=kNs, (2)
注: 每个窗口函数,是一个波形,有矩形或者高斯波形.
由于,为了丢弃该冗余频域信息,只提取频域中的前半个频率轴,即k∈[0,N/2]。 将k = N/2 带入上式,可得:
f = N 2 ∗ s N = s 2 f = \frac{N}{2}* \frac{s}{N} = \frac{s}{2} f=2N∗Ns=2s
2.2 任意频率范围的DFT
由于k是一个从零到窗口长度一半的整数,DFT只能分辨有限数量的不同频率。
例如,
如果采样率为44100Hz,
并且窗口长度为2048,
则DFT内核的归一化频率为k=[0,1,2,…,1024],
其对应于频率为f=[0,21.53,43.07,…,22050]Hz的DFT内核(使用(2))。
此设置下的频率分辨率为21.53Hz。通过 s N \frac{s}{N} Ns 得到,频率分辨率。
相比之下,钢琴键盘上最低的两个音符是A0=27.5 Hz和
a#0=29.14 Hz。在它们之间的差小于2Hz的情况下,
1024个频率bin的DFT不足以解析正确的音符。
该分辨率可以通过增加窗口大小N来提高,但是,
增加窗口大小会导致时间分辨率∆t降低,如(4)所示。
因此,我们不得不根据(5)在时间和频率分辨率之间做出妥协.
注意, 这里指出了我们可以不用必须满足, 基向量的正交集合方式。
DFT变换矩阵的向量是长度为N的所有复向量集合的基础。这意味着在应用DFT之后应用逆DFT会导致原始信号的完美重建。
可逆性对于许多信号处理应用来说很重要,
但在语音识别和声音分类等信息检索应用中,并不总是需要使用可逆的时频变换。 在这种情况下,我们可能希望以不再导致基向量的正交集合的方式修改DFT。
修改DFT的一种方法是改变基向量的频率,以增加或减少频谱的某些部分中的仓的数量。
为了实现方程(2)中s/N的非整数倍的线性标度频率,我们可以用σ(k)=Ak+B代替k,其中A和B是两个常数。
为了找到A和B,设fe和fs是我们想要分析的范围的结束和开始频率,并应用(2)得到(6),其中μ∈[0,N/2+1]是选择在频谱图中显示的仓的数量。
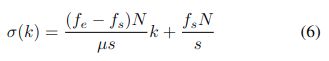
同样,我们可以通过使用 δ ( k ) = B e A k \delta(k) = B e^{Ak} δ(k)=BeAk为对数频谱图生成基向量,
从而得到 A = f s N / s A = f_sN/s A=fsN/s,
B = l n f e f s μ B = \frac{ln\frac{f_e}{f_s} }{\mu} B=μlnfsfe,如下面的(7)所示。
请注意,我们在这里非正式地使用了“basis”一词。
这些公式不能保证向量的线性独立集合,因此我们从这种方法中得到的基实际上可能是秩亏的。当使用(7)或(6)时,(1)变为(8)。这种更通用的时频变换使我们能够将频谱图的分辨率集中在最需要的频率范围内。
例如,
如果我们的起始频率为fs=50Hz,
结束频率为f=6000Hz,
则线性频率DFT核将具有归一化频率σ(k∈[01024])=[2.32,2.59,2.86,…,278.10278.36]的基向量。
这对应于频率f=[50,55.8,61.6,…5988,5994]Hz。在不改变变换窗口大小的情况下,频率分辨率从21.53Hz提高到5.8Hz。
请注意,此方法仅更改相邻频率箱中心之间的间距,而不影响 bin 本身的宽度。
因为每个 bin 代表一个固定宽度区域的一系列频率,以 (2) 中给出的 fa 为中心,如果我们将 bin 空间得太远,我们将丢失信息。
在下一节中,我们将解释(1)中的 DFT 和(8)中的可变分辨率 如何使用卷积神经网络计算短时间傅里叶变换。频率比例因子将集成到我们基于神经网络的框架中的输入特征之一中。
3. 基于神经网络的框架
在本节中,我们将讨论如何使用一维卷积神经网络计算短时傅里叶变换(STFT)、Mel谱图和constantQ变换(CQT)。然后在PyTorch中实现这些库(nnAudio)。
本文假设读者对卷积神经网络有基本的了解。对cnn的详细解释超出了本文的范围。强烈鼓励读者查阅这些论文[42,43],以便快速掌握这一领域的背景知识。我们也非常鼓励读者访问我们的github页面,以获取我们实现的详细信息。
基于神经网络的方法意味着我们将已知的音频处理知识(上面讨论的算法)编码到神经网络的神经元中,使神经网络的行为与原始算法相同。STFT是两者的基本操作,Mel谱图计算和CQT。
为了将STFT谱图转换为梅尔谱图,我们简单地将谱图乘以梅尔滤波器组核。类似地,CQT的计算也从STFT开始,然后是CQT内核的乘法。在本节开始时,我们将解释如何使用卷积神经网络来计算STFT
3.1 stft
短时间傅里叶变换(STFT),也称为滑动窗口DFT,是指在执行变换之前将信号切割成短窗口,而不是对整个信号[44]进行一次大变换的DFT应用。对于音频分析应用程序,这是应用DFT的标准方法。
STFT通常使用Cooley-tukey快速傅里叶变换算法(FFT)计算,这是首选的,因为它在O(N log N)操作中计算DFT,而对于规范的DFT实现则是 O ( n 2 ) O(n^2) O(n2)。
然而,当底层平台支持快速向量乘法时,对于较小的N值,
O ( n 2 ) O(n^2) O(n2) DFT的实现通常优于 O ( N l o g N ) O(N log N) O(NlogN) FFT。
当计算在GPU上并行完成时尤其如此。
由于神经网络库通常包含快速gpu优化的卷积函数,我们可以通过将DFT中的向量乘法表示为一维线性卷积运算,在这些平台上快速计算规范的DFT。
3.1.1 stft
核h与信号x的离散线性卷积定义如下:
( h ∗ x ) [ n ] = ∑ m = 0 M − 1 x [ n − m ] h [ m ] , ( 9 ) (h * x)[n] = \sum_{m=0}^{M-1} x[n-m]h[m] , (9) (h∗x)[n]=m=0∑M−1x[n−m]h[m],(9)
其中M是核h的长度。PyTorch定义了一个带stride参数的卷积函数。x与h的一维卷积,步长设为k,用符号* k表示,
( h ∗ k x ) [ n ] = ∑ m = 0 M − 1 x [ k n − m ] h [ m ] , ( 10 ) (h *^k x)[n] = \sum_{m=0}^{M-1} x[kn-m]h[m] , (10) (h∗kx)[n]=m=0∑M−1x[kn−m]h[m],(10)
我们可以使用卷积和步幅来实现基于GPU的短时间傅立叶变换(STFT)的快速实现。为此,我们将DFT的每个基向量作为滤波器核h,并计算与输入信号x的卷积.
为此,我们将DFT的每个基向量作为滤波器核h,并为每个基向量计算输入信号x的卷积。
我们根据我们想要在每个 DFT 窗口之间拥有的重叠量设置步幅值。
注意, 这里给出了, 当使用时间注意力机制的时候, 可以设置成0重叠,进行实验。
例如,对于零重叠,我们将步幅设置为 N,即 DFT 的长度;对于 1/2 窗口重叠,我们将步幅设置为 N/2。
请注意,由于卷积是在 (9) 中定义的方式和 (10) 计算数组索引的方式,我们需要在创建卷积核时反转 DFT 基向量中的元素顺序。以下表达式是卷积核对 ( h r e [ k , n ] 和 h i [ k , n ] h_{re}[k, n] 和 h_i [k, n] hre[k,n]和hi[k,n])
分别表示第k个DFT基向量的实部和虚部:
DFT通常用一个函数来计算,该函数将每个窗口边缘的样本平滑地淡入零,以避免通过在边缘[45]上突然切割窗口而引入的高频伪影。
DFT 窗函数的典型例子包括 Hann、Hamming 和 Blackman 类型。
在基于 GPU 的 DFT 实现中,使用具有步幅 (10) 的卷积函数,我们可以在进行卷积之前将这些窗口函数elementwise 与滤波器内核 hi 和hr 相乘来有效地实现窗口平滑。
这里表明,在gpu中,我们实现窗函数的功能,是通过, 将原来的窗函数元素 乘上 两个一位的卷积核, h r h_r hr代表实部的一维卷积核, h i h_i hi代表虚部的一维卷积核。
在计算频谱图时,我们通常使用长度为 N = 2048 或 N = 4096 的离散傅里叶变换,但 N 的其他值是可能的。我们经常切割 DFT 窗口,以便它们按一定数量相互重叠以提高时间分辨率。
在具有 T windows 的信号中,我们让 X t X_t Xt 是索引 t ∈ [0, T -1] 处窗口的 DFT。索引 t 处窗口的时间域表示将由 xt 表示。
图 2 显示了基于神经网络的 stft 的示意图。
使用 PyTorch 1D 卷积神经网络实现 短文本有两个主要优点。
- 首先,它支持批量处理。使用神经网络的框架,我们可以使用张量操作将音频剪辑的张量转换为频谱图张量。
- 其次,神经网络权重可以是固定的或可训练的。我们将在第 VB 节讨论可训练 短视滤波内核如何提高频率预测精度。
3.1.2 stft 的nn.Audio接口
STFT在nnAudio中实现为函数Spectrogram。
STFT(),具有默认参数:
n_fft = 2048,freq_bins = None,hop_length = 512,
window = 'hann',freq_scale = 'no',center = True,pad_mode = 'refect', fmin = 50,fmax = 6000,sr = 220,可训练 = False。
该函数有一个可选的参数 freq_scale,允许用户选择线性或对数频率 bin 尺度。
3.2 Mel 语谱图
Stevens 等人在 1937 年提出了 Mel 频率尺度,试图量化音高,使得 Mel 尺度音高的相等差异对应于感知音高的相等差异,而不管赫兹的频率 [46]。除了 Stevens 等人提出的原始 Mel 量表外,还有其他几项尝试获得 Mel 量表的修改版本 [47-49]。因此,Mel 量表没有单一的“正确的”公式,因为文献中存在各种不同的公式 [50]。
传统的 Mel 尺度转换频率是Shaughnessy 的书 [51],它在 HTK 语音识别工具包 [52] 中实现为 (13)),
我们将此形式称为“htk”,如下所示:
等式(14)显示了 MATLAB 53 和 librosa(python 音频处理库)[23] 在 Aducery Toolbox 中使用的另一种形式。这种形式是准对数的,这意味着 Mel 尺度转换的频率在低频区域(通常是断点设置为 1,000Hz)中是线性的,并在高频区域(断点之后)中对数。
注意,这里指明,需要根据自己的任务,选取是否应该在1000Hz 以下使用线性的,
librosa 的默认 Mel 量表采用 (14) 的形式,但可以通过将 htk 参数设置为 True 将其更改为 (13) 中定义的形式。
3.2.1 Mel spec
一旦我们的频率到 Mel 尺度转换,我们可以创建 Mel 滤波器组(有关 Mel 滤波器组计算的详细信息,读者可以参考 [54]),这些滤波器组乘以 STFT 结果的每个时间步以获得 Mel 频谱图 [55]。这种转换的一个例子如图3所示,它描述了从25Hz、75Hz、150Hz、400Hz和450Hz的五个纯音调开始的信号的STFT和Mel尺度谱图(如图A区域所示)。
( 这里,作者可能是笔误了)
0.25 秒后,三个音调停止,仅留下 2 个音调,75Hz 和 450Hz(如 B 区域所示)。经过另外 0.25 秒后,只剩下 75Hz 音调(区域 C),最后,它以单个 450Hz 音调(区域 D)结束。STFT谱图如图3左侧所示。
在本例中,STFT的窗口大小为128个样本,这将生成一个128个频率箱的谱图。由于对称性,完整的频谱图包含冗余信息,因此最终 STFT 结果中只使用了 65 个 bin。STFT 的hop size 为 32 个样本,等于窗口大小的四分之一。
为了获得具有四个 Mel bin 的 Mel 频谱图,我们需要有四个 Mel 滤波器组。Mel滤波器组的基函数形状为三角形,通过将多个STFT bin分组到单个Mel bin,将原始STFT转换为Mel谱图的核。
图 3 中示例的精确映射如表 1 所示。区域 A 中有五个频率分量,对应于 25 Hz、75 Hz 和 150 Hz 的三个频率分量将映射到 Mel bin 0。由于 Mel 滤波器组相互重叠,频率分量 150 Hz 也映射到 Mel bin 1,而两个高频分量 400 Hz 和 450Hz 只会映射到 Mel bin 3。
每个时间步都以相同的方式乘以 Mel 滤波器组矩阵,获取 Mel 频谱图。
nnAudio在PyTorch中从原始波形中提取梅尔谱图的实现相对简单。我们使用第III-A节中描述的PyTorch1D卷积神经网络获得STFT结果,然后使用从librosa获得的Mel滤波器组。
(注意, 这里可以设置htk= False, 用来保证1kHz 以下,使用线性的方式)
默认情况下,librosa 复制了 Slaney []_ 完善的 MATLAB 听觉工具箱的行为。根据此默认实现,从赫兹到梅尔的转换在 1 kHz 以下是线性的,在 1 kHz 以上是对数的。
另一个可用的实现根据以下公式复制隐马尔可夫工具包 []_ (HTK):mel = 2595.0 np.log10(1.0 + f 700.0)。实现的选择由“htk”关键字参数决定:设置“htk=False”会导致听觉工具箱实现,而设置“htk=True”会导致HTK实现。
Mel滤波器组的值用于初始化单层全连接神经网络的权重。
幅度STFT的每个时间步长被前馈到这个用Mel权重初始化的完全连接层中。初始化神经网络时,只需创建一次Mel滤波器组。这些权重可以设置为可训练的或保持固定,非常类似于第III-A节中讨论的STFT的神经网络实现。
上图显示了我们PyTorch实现Mel谱图计算的示意图。
3.2.2 Mel spec 的nn Audio接口
nnAudio将Mel谱图层实现为spectrogram.MelSpectrogram(),
默认参数为:sr=22050,n_fft=2048,n_mels=128,
hop_length=512,window=“hann”,center=True,
pad_mode=“reflect”,htk=False,fmin=0.0,fmax=None,
norm=1,trainable_Mel=False,trainable_STFT=False。
3.3 常数Q 变换;
4. 实验结果
5. 应用实例
5.1探索不同的输入表示
在本节中,我们将讨论这项工作的一个可能应用,即音乐转录 [66, 67]。我们将表明,使用 nnAudio,可以快速探索不同类型的频谱图作为神经网络的输入,并轻松选择产生最佳转录准确度的频谱图。
考虑以下场景:我们想进行复音音乐转录,我们选择了一个特定的模型(完全连接的神经网络)来解决这个任务,但我们想知道哪些输入频谱图表示将为这项任务产生最佳结果 8] 。在我们的实验中,总共探索了四种类型的频谱图:线性频率尺度频谱图 (LinSpec)、对数频率尺度频谱图 (LogSpec)、梅尔频谱图 (MelSpec) 和 CQT。此外,这些表示中的每一个都将具有不同的参数设置,我们需要考虑。对于 LinSpec 和 LogSpec,我们想探索五种不同大小的傅立叶内核。对于 MelSpec,我们将探索四种不同大小的傅立叶内核,对于这些内核中的每一个,Mel 滤波器组的数量都会有所不同。最后,对于 CQT,将检查每个八度八度的十个不同箱。这意味着总共有 34 种不同的输入表示。
5.2 可训练的转换KERNELS
因为我们使用一维卷积神经网络实现STFT和MelSpec,其中神经元权重对应于傅立叶核和梅尔滤波器组,因此可以通过梯度下降进一步微调这些核和滤波器组以及模型。该技术可用于使用神经网络实现的所有转换,但我们将在本小节中只关注讨论 STFT 和 MelSpec 作为一个例子。
考虑以下任务:给定一个纯正弦波,我们需要训练一个能够返回信号频率的模型。为了使这项任务变得不那么繁琐,STFT窗口的大小被故意设置为一个很小的数字(64),这样输出的频谱图的频率分辨率就很差。纯正弦波的频率为200Hz ~ 22,050hz(奈奎斯特频率)之间的整数。换句话说,我们只有33个频率箱来代表从20hz到20khz的整个声音频谱。
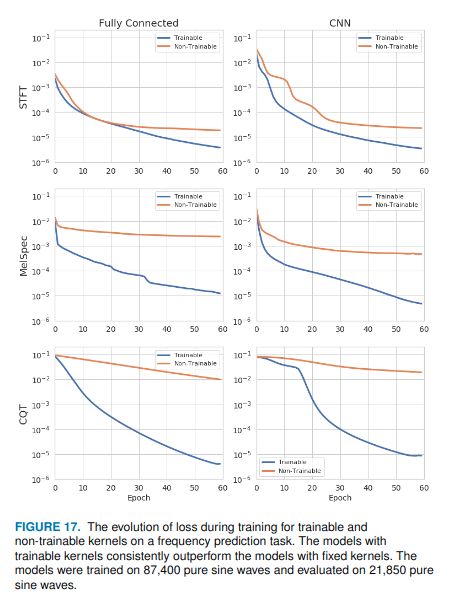
我们的实验中,我们产生了10925个不同频率(200-22050Hz)的纯正弦波。对于每个频率,我们生成10个不同相位的纯正弦波。总共生成了109250个纯正弦波来形成我们的数据集。这些正弦波中的80%用作训练集,其余20%用作测试集。我们探讨了可训练内核是否能够提高模型的准确性。我们专注于预测输入符号波频率的两个模型:全连接网络和2D卷积神经网络(CNN)。对于完全连接的网络,我们使用一层一个神经元和S形激活。频谱图被平坦化为1D向量,并用作模型的输入。对于CNN,使用两个2D卷积层,每层的内核大小(4×4)。CNN的最终特征图被平坦化,并被前馈到具有一个神经元和S形激活的完全连接的网络。nnAudio被用作这些模型的第一层,用于将波形转换为标准频谱图、Mel频谱图或CQT频谱图。我们将第一层设置为可训练的,并将由此产生的损失与该层设置为不可训练的相同模型进行比较。
如图17所示,可训练变换层导致STFT、MelSpec和CQT层以及线性和CNN模型的均方误差(MSE)较低。
为了解释可训练的STFT、MelSpec和CQT层如何提高预测精度,我们需要研究经过训练的傅立叶核和Mel滤波器组。图18中的前两行显示了滤波器组为k=1,2时的傅立叶基。由于完全连接模型的结果与CNN模型非常相似,因此我们在此仅报告CNN模型的结果。左边的列将原始傅立叶核可视化,右边的列将训练后的傅立叶核可视化。尽管经过训练的傅立叶核的总体形状与原始傅立叶核相似,但它在核的基频之上包含一些更高的频率。这些额外的频率可以允许经由STFT提取更多的信息。训练后的STFT频谱图显示在同一图的最后一行。从图中可以清楚地看出,它在基频附近有更多的泛音样信号,而原始STFT对纯正弦波输入显示出非常干净的响应。经由训练的STFT获得的频谱图可以能够向神经网络提供关于输入信号的输入频率的线索。经过训练的Mel滤波器组也是如此CQT内核,
如图19和20所示。通过允许神经网络进一步训练或微调Mel滤波器组和CQT内核,我们可以获得更丰富的频谱图。这为频率预测模型提供了更多的信息,从而达到较低的MSE损失,而与网络架构无关。该小节表明,用nnAudio进一步训练或微调频谱图转换层会导致较低的MSE损失。尽管该分析使用了一个简单的、人工生成的数据集,但它仍然提供了一个很好的例子,说明如何通过可训练的转换层获得更高性能的端到端模型。详细的实验结果可在nnAudiogithub存储库中获得。
6 conclusion
我们提出了一种利用神经网络实时提取不同类型谱图的新框架。这种方法允许人们动态地训练核(包括傅里叶核、Mel滤波器组和CQT核),作为更大的神经网络训练的一部分,专门适应于手头的问题。我们的方法已经实现为基于gpu的库nnAudio。
不同的时域到频域变换算法,如短时傅里叶变换、Mel谱图和常数q变换,已经在开源机器学习库PyTorch中实现。我们利用PyTorch的CUDA集成,实现基于GPU的快速音频处理。在我们的实验中,我们发现GPU音频处理将1770个波形转换为频谱图的时间从10.6秒缩短到短时间傅里叶变换(STFT)的0.001秒;Mel谱图从18.3秒到0.015秒;从103.4秒到0.258秒的常量q变换(CQT)。这些实验是在三台不同的机器上进行的:两台台式机分别使用GTX 1070和RTX 2080 Ti,一台DGX工作站使用Tesla v100 GPU。尽管初始化转换层(将傅里叶内核从RAM传输到GPU内存)需要一些时间(大约5秒),但一旦GPU内存上的一切都准备就绪,单个频谱图的处理时间就以微秒为单位,使得初始化时间在训练神经网络时可以忽略不计。
此外,我们提出的基于神经网络的音频处理框架允许可训练和可细化的傅里叶核,Mel滤波器组,甚至CQT核。V-B节中讨论的一个实验证实,与不可训练的核相比,可训练的核在频率预测任务上产生更好的最终模型。
最后,我们提出了一种神经网络方法来计算不同版本的CQT(直接计算,下采样方法,以及通过去除频域内核)。据我们所知,我们提出的框架是第一个支持CQT的基于神经网络的音频处理工具箱。在比较不同基于神经网络的CQT算法的计算速度时(图11(b)),我们发现(在章节III-C5中),使用时域CQT内核的CQT算法比常用的基于频域内核的CQT算法执行得更快[7,60]。因此,在我们提出的基于GPU神经网络的框架中,将1770个波形转换为频谱图的CQT计算速度从0.258大幅降低到仅0.001。当将nnAudio应用到一个真实的数据集MusicNet时,它显著地将计算时间从983分钟减少到99分钟。
为了使我们提出的GPU音频处理工具便于其他研究人员使用,我们将上面讨论的所有算法组合到一个用户友好的PyPI包中,称为nnAudio