树形DP模型与题目详解acm
树形DP问题
- #写在前面
-
- ##没有上司的舞会
-
- ----c++版
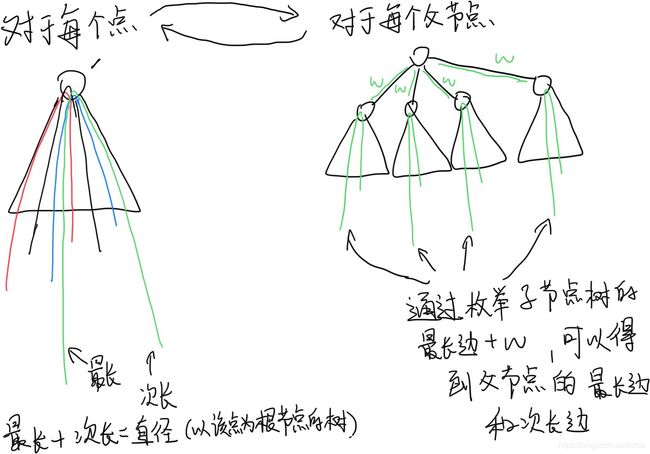
- ##树的最长路径
-
- ----c++版
- ##树的中心
-
- ----c++版
- ##数字转换
-
- ----c++版
- ##二叉苹果树
-
- ----c++版
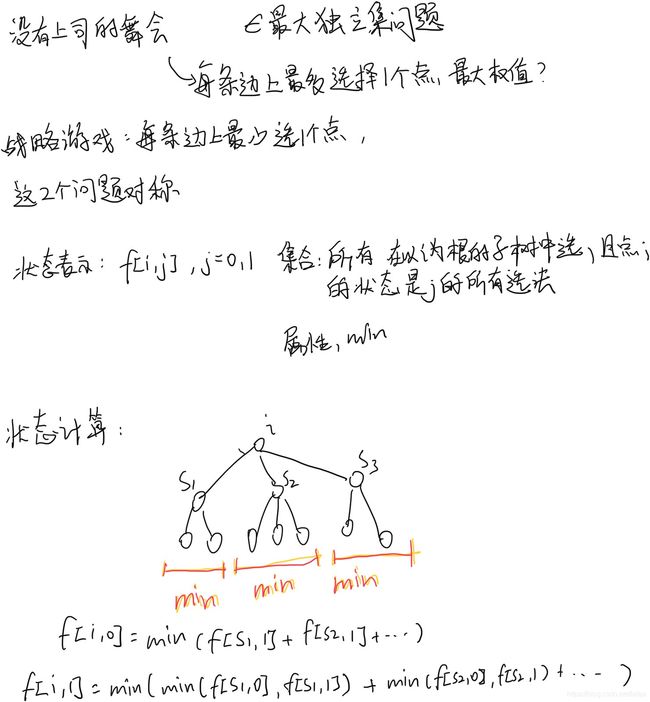
- ##战略游戏
-
- ----c++版
- ##皇宫看守
-
- ----c++版
#写在前面
##没有上司的舞会
https://www.acwing.com/problem/content/287/
这里用了状态机
----c++版
#include##树的最长路径
https://www.acwing.com/problem/content/1074/
经典找树的直径


如果边有负的权值,则需要树形dp
想办法把所有边枚举一遍,选出最大的
----c++版
//树的最长路径也可以称为树的直径
#include##树的中心
https://www.acwing.com/problem/content/1075/
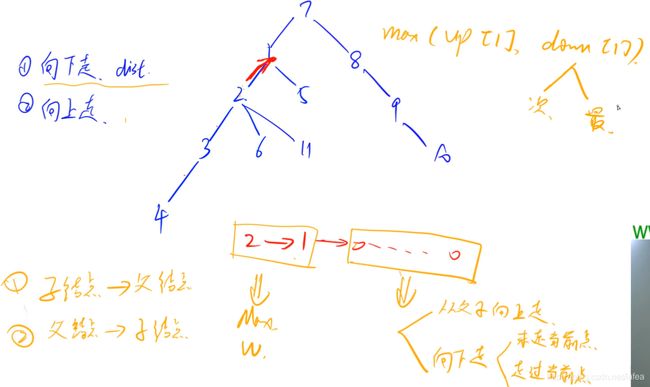
向上走就是求一个点的父节点的不走该节点的最长路径,其实我们知道了每一个节点向下走的长度就可以知道向上的最长路径了,一个子节点 j 的向上最长路径就是 它的父节点 u 的最长向上路径和最长向下路径取最大值,如果向下最长路径经过了 j 就改为第二长的向下路径
----c++版
//直观上看起来有点像中心
#include##数字转换
https://www.acwing.com/problem/content/1077/

----c++版
#include##二叉苹果树
https://www.acwing.com/problem/content/1076/
----c++版
#include##战略游戏
https://www.acwing.com/problem/content/325/
极大独立集及其相关概念:
https://blog.csdn.net/Richard_for_OI/article/details/79520470
----c++版
#include##皇宫看守
https://www.acwing.com/problem/content/1079/
----c++版
#include