回溯算法总结
首先回溯算法本身还是一个纯暴力的算法,只是回溯过程可能比较抽象,导致大家总是感觉看到的相关题目做的不是很顺畅,回溯算法一般来说解决的题目有以下几类:
组合问题:lq77、lq17、lq39、lq40、lq216、
切割问题:lq131、lq93、
子集问题:lq78、lq90、
排列问题:lq46、lq47、
棋盘问题:lq51、lq37、
其他类:lq491、lq332、
在回溯算法中,所有的问题都可以抽象为一个树形结构
回溯算法四部曲:
1、递归函数、参数、返回值
2、确定终止条件
3、单层递归逻辑
4、剪枝操作(一般在for中i的遍历范围做控制)
回溯算法模板:
//回溯算法模板
public class HuiSu {
LinkedList path = new LinkedList<>();
List> result = new ArrayList<>();
//功能函数,调用backtracking()
public List> main(String[] args) {
backtracking(1);
return result;
}
public void backtracking(int startindex){
// if(终止条件){
// 1、收集结果
// return;
// }
// for(int i=startindex;i 下面我们来看具体的题目:
组合问题:
lq77:组合问题
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例
输入:n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
答案:我们按照回溯算法的模板,即可完成这道题目的代码部分。
class Solution {
LinkedList path = new LinkedList<>();
List> result = new ArrayList<>();
public List> combine(int n, int k) {
backtracking(n,k,1);
return result;
}
public void backtracking(int n,int k,int startindex){
if(path.size() == k){
result.add(new ArrayList<>(path));
return;
}
for(int i = startindex; i<=n-(k-path.size())+1; i++){
path.add(i);
backtracking(n,k,i+1);
path.removeLast();
}
}
} lq216:组合总和III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例:
输入:k = 3, n = 7 输出: [[1,2,4]] 解释: 1 + 2 + 4 = 7 没有其他符合的组合了。
答案:
class Solution {
LinkedList path = new LinkedList<>();
List> result = new ArrayList<>();
public List> combinationSum3(int k, int n) {
backtracking(0,k,n,1);
return result;
}
public void backtracking(int targetsum,int k,int n,int startindex){
if(targetsum>n){
return;
}
if(path.size()==k){
if(targetsum==n){
result.add(new ArrayList<>(path));
return;
}
}
for(int i=startindex;i<=9-(k-path.size())+1;i++){
targetsum = targetsum+i;
path.add(i);
backtracking(targetsum,k,n,i+1);
targetsum = targetsum-i;
path.removeLast();
}
}
} lq17:电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例:
输入:digits = "23" 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
注解:这道题目和前面两道题目有区别,前面两道题目是在一个集合中选取字符进行组合,这道题目中是在两个集合中分别选取,所以单层遍历时候不用startindex来控制,而需要转化为每个数字代表的字符个数来控制。
答案:
class Solution {
StringBuilder path = new StringBuilder();
List result = new ArrayList<>();
//初始对应所有的数字,为了直接对应2-9,新增了两个无效的字符串""
String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public List letterCombinations(String digits) {
if (digits == null || digits.length() == 0) {
return result;
}
backtracking(digits,0);
return result;
}
public void backtracking(String digits,int num){
if(num == digits.length()){
result.add(path.toString());
return;
}
String str = numString[digits.charAt(num) - '0'];
for(int i=0;i lq39:组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
分析:此题目要进行剪枝操作,首先在sum+当前值之后大于target时,应该直接剪枝,其次,此题单层遍历时,当前值是可以重复的,但不代表不需要startindex,只是startindex在调用时不需要+1操作,因为如果没有startindex,就会造成重复。
//lq39.组合总和
class Solution {
LinkedList path = new LinkedList<>();
List> result = new ArrayList<>();
public List> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates); // 先进行排序
backtracking(candidates,target,0,0);
return result;
}
public void backtracking(int[] candidates, int target, int sum, int startindex){
if(sum==target){
result.add(new ArrayList<>(path));
return;
}
for(int i = startindex;i target) break;
sum=sum+candidates[i];
path.add(candidates[i]);
backtracking(candidates,target,sum,i);
sum=sum-candidates[i];
path.removeLast();
}
}
} lq40:组合总和II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
分析:此题中和其他题目不同的是需要判断如果两个数字相同的情况如何剪枝,此时需要用一个boolean[] used来标志此位是否遍历过,然后进行剪枝。此时剪枝时要注意used[i-1]==flase而不是true,因为我们此处想剪的是树形结构的一整个分支,如果是true的话是第一个树枝的下一层。
答案:
//lq40.组合总和II
class zuheZHII{
LinkedList path = new LinkedList<>();
List> result = new ArrayList<>();
boolean[] used;
public List> combinationSum2(int[] candidates, int target) {
used = new boolean[candidates.length];
Arrays.fill(used, false);
Arrays.sort(candidates);
backtracking(candidates,target,0,0);
return result;
}
public void backtracking(int[] candidates, int target,int sum, int startindex){
if(sum == target){
result.add(new ArrayList(path));
return;
}
for(int i = startindex;itarget){
break;
}
if(i>0 && (candidates[i]==candidates[i-1]) && (used[i-1]==false)){
continue;
}
used[i] = true;
sum = sum+candidates[i];
path.add(candidates[i]);
backtracking(candidates,target,sum,i+1);
sum = sum-candidates[i];
used[i] = false;
path.removeLast();
}
}
public static void main(String[] args) {
zuheZHII z = new zuheZHII();
int[] candidates = {10,1,2,7,6,1,5};
List> res = z.combinationSum2(candidates,8);
System.out.println(res);
}
} lq131:分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例:
输入:s = "aab" 输出:[["a","a","b"],["aa","b"]]
分析:此题比较重要的是如何确定终止条件?当遍历标志位startindex>s.length()时,说明得到一个分割方案了,此时就可以回收path了,这个点和之前的组合问题不同,需要注意,然后就是判断回文串的时候需要注意一些,其他问题都和模板一致。
答案:
//lq131.分割回文串
class huiwenchaun {
List> lists = new ArrayList<>();
Deque deque = new LinkedList<>();
public List> partition(String s) {
backTracking(s, 0);
return lists;
}
private void backTracking(String s, int startIndex) {
//如果起始位置大于s的大小,说明找到了一组分割方案
if (startIndex >= s.length()) {
lists.add(new ArrayList(deque));
return;
}
for (int i = startIndex; i < s.length(); i++) {
//如果是回文子串,则记录
if (isPalindrome(s, startIndex, i)) {
String str = s.substring(startIndex, i + 1);
deque.addLast(str);
} else {
continue;
}
//起始位置后移,保证不重复
backTracking(s, i + 1);
deque.removeLast();
}
}
//判断是否是回文串
private boolean isPalindrome(String s, int startIndex, int end) {
for (int i = startIndex, j = end; i < j; i++, j--) {
if (s.charAt(i) != s.charAt(j)) {
return false;
}
}
return true;
}
public static void main(String[] args) {
huiwenchaun h = new huiwenchaun();
String s = "aab";
List> str = h.partition(s);
System.out.println(str);
}
} lq93:复原IP地址
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "[email protected]" 是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。
示例:
输入:s = "25525511135" 输出:["255.255.11.135","255.255.111.35"]
分析:此题相对比较难,因为需要这样想,切分IP地址的时候要加".",所以终止条件就是"."的个数,并且需要判断是否符合IP地址的规定。
答案:
class Solution {
List str = new ArrayList<>();
public List restoreIpAddresses(String s) {
if(s.length()>12) return str;
backTracking(s,0,0);
return str;
}
// startIndex: 搜索的起始位置, pointNum:添加逗点的数量
private void backTracking(String s, int startIndex, int pointnum) {
if(pointnum == 3){// 逗点数量为3时,分隔结束
// 判断第四段⼦字符串是否合法,如果合法就放进result中
if(isPalindrome(s,startIndex,s.length()-1)){
str.add(s);
}
return;
}
for(int i = startIndex;i end) {
return false;
}
if (s.charAt(start) == '0' && start != end) { // 0开头的数字不合法
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s.charAt(i) > '9' || s.charAt(i) < '0') { // 遇到⾮数字字符不合法
return false;
}
num = num * 10 + (s.charAt(i) - '0');
if (num > 255) { // 如果⼤于255了不合法
return false;
}
}
return true;
}
} lq78:子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
分析:此题属于子集问题,相对于组合问题不同的是收集结果的时间不同,组合问题收集的是所有的叶子节点,而子集问题是收集所有的节点。
答案:
//lq78.子集
class ZJ {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
public List> subsets(int[] nums) {
backtracking(nums,0);
return result;
}
public void backtracking(int[] nums,int startindex){
result.add(new ArrayList<>(path));
if(startindex>=nums.length){
return;
}
for(int i=startindex;i> res = z.subsets(candidates);
System.out.println(res);
}
} lq90:子集II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例:
输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
分析:此题和lq40.组合总和II比较类似,主要难点在于剪枝,剪枝过程和lq40.组合总完全一致
答案:
//lq90.子集II
class ZJII {
LinkedList path = new LinkedList<>();
List> result = new ArrayList<>();
boolean[] used;
public List> subsetsWithDup(int[] nums) {
used = new boolean[nums.length];
Arrays.fill(used,false);
Arrays.sort(nums);
backtracking(nums,0);
return result;
}
public void backtracking(int[] nums,int startindex){
result.add(new ArrayList<>(path));
if(startindex >= nums.length){
return;
}
for(int i=startindex;i0 && nums[i]==nums[i-1] && used[i-1]==false){
continue;
}
used[i]=true;
path.add(nums[i]);
backtracking(nums,i+1);
used[i]=false;
path.removeLast();
}
}
public static void main(String[] args) {
ZJII z = new ZJII();
int[] candidates = {1,2,2};
List> res = z.subsetsWithDup(candidates);
System.out.println(res);
}
} 【重要】lq491:递增子序列
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例:
输入:nums = [4,6,7,7] 输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
分析:
此题比较重要,同样也比较困难一些,此题的难度在于剪枝和判断递增,此处的剪枝本身还是去重,和前面的题目类似,只是前面的组合或者其他题目可以通过对数组排序,保证相同的数连在一起,所以可以通过boolean[]数组来记录,此题通过简单的数组下标并不能控制,所以需要借助HashMap来控制是否重复的问题。此题在回溯算法中相对比较全面。
还有一个重要的点就是终止条件后的return;并不是每道题目的终止条件后面都要return,因为此题目的终止条件并不是不在遍历,只有当收集的是叶子节点为终止条件时才需要加return,其他时候不需要,因为终止条件只是要收集结果,并不是遍历结束。
//lq491.递增子序列
class DZZXL{
LinkedList path = new LinkedList<>();
List> result = new ArrayList<>();
public List> findSubsequences(int[] nums) {
backtracking(nums,0);
return result;
}
public void backtracking(int[] nums,int startindex){
if(path.size()>=2){
result.add(new ArrayList<>(path));
}
HashMap map = new HashMap<>();
for(int i=startindex;i> res = z.findSubsequences(candidates);
System.out.println(res);
}
} lq46:全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
答案:
class Solution {
LinkedList path = new LinkedList<>();
List> result = new ArrayList<>();
boolean[] used;
public List> permute(int[] nums) {
used = new boolean[nums.length];
Arrays.fill(used,false);
backtracking(nums,used);
return result;
}
public void backtracking(int[] nums,boolean[] used){
if(path.size()==nums.length){
result.add(new ArrayList<>(path));
return;
}
for(int i=0;i lq47.全排列II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例:
输入:nums = [1,1,2] 输出: [[1,1,2], [1,2,1], [2,1,1]]
分析:
此题目主要还是去重,和前面lq40.组合总和的方法基本一致,需要你注意的就是判断,当used[i]==true时,需要跳过此次遍历,否则会造成重复。其他的都是基本操作。
答案:
//lq47.全排列II
class QPLII{
LinkedList path = new LinkedList<>();
List> result = new ArrayList<>();
boolean[] used;
public List> permuteUnique(int[] nums) {
used = new boolean[nums.length];
Arrays.fill(used,false);
Arrays.sort(nums);
backtracking(nums,used);
return result;
}
public void backtracking(int[] nums,boolean[] used){
if(path.size()==nums.length){
result.add(new ArrayList<>(path));
return;
}
for(int i=0;i0 && nums[i]==nums[i-1] && used[i-1]==false){
continue;
}
if(used[i]==true){
continue;
}
used[i] = true;
path.add(nums[i]);
backtracking(nums,used);
used[i] = false;
path.removeLast();
}
}
public static void main(String[] args) {
QPLII q = new QPLII();
int[] candidates = {1,1,2};
List> res = q.permuteUnique(candidates);
System.out.println(res);
}
} lq51:N皇后问题
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例:
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
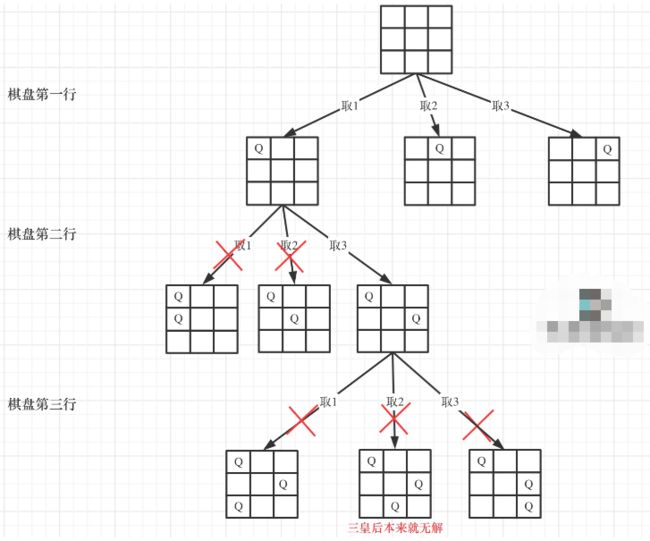
分析:此题目是回溯算法中相对比较难的题目,主要原因是不知如何将问题转化为回溯算法来进行解决,我们可以通过以下树形结构图来分析此题目。
所以此题的树形结构深度就是棋盘的行数是,树形结构的宽度就是棋盘的宽度
在for(int col=0;col 此题目还需要注意的一个点是,我们需要自己构建一个二维数组作为棋盘结构,然后还需要一个函数来判断当前棋盘是否符合条件。最重要的一点是,题目要求的返回值是一个二维数组,所以每一种成功的棋盘布局需要转换成一个一维数组,多个成功的棋盘构成最终答案,所以还需要一个函数将棋盘结构转换成一维数组。 答案://lq51.N皇后问题
class NQueen {
List