【C++】动态规划题解集(更新至数位DP)

数字三角形模型

1015.摘花生

题目链接：1015.摘花生.
*** 题目描述***
一个nxm的矩阵，起点 （0，0） 终点 （n，m），给定（x，y）上物品价值w，只能 向右 or 向下，求经过的 最大价值
题目分析
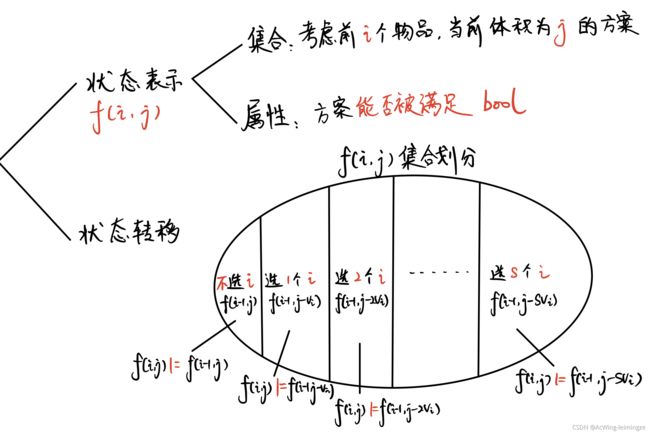
状态表示：f[i][j]
属性：从起点出发，走到第i行第j列的所有方案
集合：MAX
状态转移f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j]
CODE

#include 
using namespace std;
const int N = 110;
int T;
int n, m;
int w[N][N];
int f[N][N];
int main()
{
	cin >> T;
	while (T--)
	{
		memset(w, 0, sizeof w);
		memset(f, 0, sizeof f);
		cin >> n >> m;
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= m; j++)
				cin >> w[i][j];
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= m; j++)
				f[i][j] = max(f[i][j - 1], f[i - 1][j])+w[i][j];
		cout << f[n][m] << endl;
	}
	return 0;
}

1018. 最低通行费

题目链接: 最低通行费.
题目描述
给定nxn的矩阵，从 （1，1） 出发，最终走到 （n,n）
走过的方块书不超过2*n-1，求走过所有方块价值的最少路线
题目分析
本题用到的是哈密顿距离，d=abs(x1-x2)+abs(y1-y2)
由此可知在2*n-1的步数内走到终点，必须向右 or 向下
状态表示：f[i][j]
属性：从起点出发，走到第i行第j列的所有方案
集合：MAX
状态转移f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j]
CODE

#include 
using namespace std;
const int N = 110;
int n;
int w[N][N];
int f[N][N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			cin >> w[i][j];
	memset(f, 0x3f, sizeof f);//init，由于需要求min，所以初始化为正无穷
	f[1][1] = w[1][1];//特判起点
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
		{
			if (i > 1)f[i][j] = min(f[i][j], f[i - 1][j]+w[i][j]);
			if (j > 1)f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);
			//等价于
			//if(i==1&&j==1)f[i][j]=w[i][j];
			//f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j];
			//这里需要特判（1，1），如果不特判（1，1）分别可以从（1，0）or（0，1）过来，这两点的值为正无穷，且f[i][j]的属性是min，f[1][1]是从这两个无穷大的数更新过来的，摘花生不用特判的原因是求得max，（1，1）无论从（1，0）or（0，1）来都是0，所以不影响结果不需要特判。
		}
	cout << f[n][n] << endl;
	return 0;
}

1027. 方格取数

题目链接: 方格取数
题目描述
给定NxN的矩阵，每个格子有价值为w的物品，从起点（1，1）到终点（n，n）从起点出发两次，如果同一个各自经过两次，则只会累加一次
求最大价值
题目分析
f[x1][y1][x2][y2][1<<(n*n)]
由此可见无论时间复杂度还是空间复杂度非常高
至此我们可对其采取优化
我们可以假设其为同时走，所以就有
x1 + y1 = x2 + y2 = k
f[k][i][j]
属性：表示路径长度为k，第一条路x1=i，第二条路x2=j的所有方案
集合:物品最大价值MAX
状态转移 f[k][i][j]=max(f[k-1][i][j],f[k-1][i-1][j],f[k-1][i][j-1],f[k-1],[i-1][j-1])+w
CODE

#include 
using namespace std;
const int N = 15;
int n;
int w[N][N];
int f[N * 2][N][N];
int main()
{
	cin >> n;
	int a, b, c;
	while (cin >> a >> b >> c, a || b || c)w[a][b] = c;
	for (int k = 2; k <= 2 * n; k++)
	{
		for (int i1 = 1; i1 <= n; i1++)
		{
			for (int i2 = 1; i2 <= n; i2++)
			{
				int j1 = k - i1, j2 = k - i2;
				if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
				{
					int& x = f[k][i1][i2];
					int t = w[i1][j1];
					if (i1 != i2)t += w[i2][j2];
					x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
					x = max(x, f[k - 1][i1][i2 - 1] + t);
					x = max(x, f[k - 1][i1 - 1][i2] + t);
					x = max(x, f[k - 1][i1][i2] + t);
				}
			}
		}
	}
	cout << f[2 * n][n][n] << endl;
	return 0;
}

275. 传纸条

题目链接: 传纸条.
题目描述
给定NxM的矩阵，A从 （1，1） 位置开始，B从 （n,m） 位置开始，A给B传纸条只能向下 or 向右 ，每个格子都有其
价值，求所经过格子的价值最大
题目分析
我们可以转换为，从（1，1）出发的两条路
线求价值最大

图片摘自：彩色铅笔%%%%
链接: 图片参考.
我们可以将交叉的路线上下交换以下，

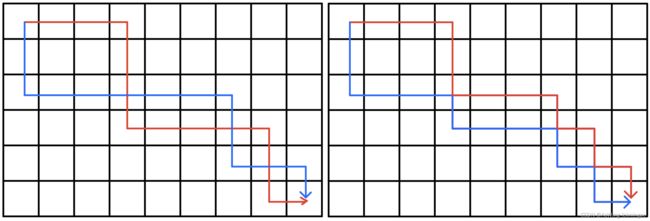
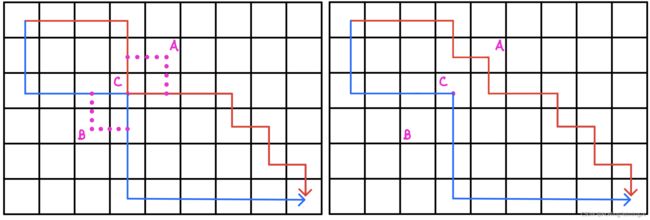
方格取数中，走到相同格子时，只会累加一次格子的价值，由于原路线是最优解，则必然wA=wB=0,否则会改变总价值.
此题中，如果走相同的点，格子只能算一次，因此就需要绕一下点，因为所有点权值非负，这样的权值和比有交点的权值大，所以有交点的路线一定不是最优解

CODE

#include 
using namespace std;
const int N = 55;
int n, m;
int w[N][N];
int f[2 * N][N][N];
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			cin >> w[i][j];
	for (int k = 2; k <= m + n; k++)
	{
		for (int i1 = 1; i1 <= n; i1++)
		{
			for (int i2 = 1; i2 <= n; i2++)
			{
				int j1 = k - i1, j2 = k - i2;
				if (j1 >= 1 && j1 <= m && j2 >= 1 && j2 <= m)
				{
					int& t = f[k][i1][i2];
					int v = w[i1][j1];
					//没有交点则权值相加，如果有交点，则取一次即可
					if (i1 != i2)v += w[i2][j2];
					t = max(t, f[k - 1][i1][i2] );
					t = max(t, f[k - 1][i1 - 1][i2]);
					t = max(t, f[k - 1][i1 - 1][i2 - 1]);
					t = max(t, f[k - 1][i1][i2 - 1]);
					t+=v;
				}
			}
		}
	}
	cout << f[n + m][n][n] << endl;
	return 0;
}

最长上升子序列模型

1017. 怪盗基德的滑翔翼

题目链接：怪盗基德的滑翔翼
题目描述
给定长度为n的一维数组w[n]，表示每个楼房的高度，怪盗基德可以选定任意一个楼房，作为他的起点位置，它可以选择向左 or 向右出发直到边界，中途不可改变方向，现在需要求出一条路径经过的高度递减长度最大
题目分析
本题是正向最长上升子序列和反向最长上升子序列的模板题，直接上code
CODE

#include 
using namespace std;
const int N = 110;
int k, n;
int w[N];
int up[N], down[N];
int main()
{
	cin >> k;
	while (k--)
	{
		memset(up, 0, sizeof up);
		memset(down, 0, sizeof down);
		cin >> n;
		for (int i = 1; i <= n; i++)cin >> w[i];
		//最长上升子序列
		for (int i = 1; i <= n; i++)
		{
			up[i] = 1;
			for (int j = 1; j < i; j++)
				if (w[i] > w[j])up[i] = max(up[i], up[j] + 1);
		}
		//反向最长上升子序列
		for (int i = n; i >= 1; i--)
		{
			down[i] = 1;
			for (int j = n ; j > i; j--)
				if (w[i] > w[j])down[i] = max(down[i], down[j] + 1);
		}
		int res = 0;
    	for (int i = 1; i <= n; i++)
    	{
	    	res = max(res, up[i]);
		    res = max(res, down[i]);
     	}
	    cout << res << endl;
	}
	return 0;
}

1014. 登山

题目连接：登山
题目描述
给定一个长度为n的数组a[n]，表示某个景点的海拔，初始海拔为0，先上山后下山，队员一旦下山，就不再往上走。
题目分析
分别求出每个点向左和向右的最长下降子序列求和，找出最长的一个。
CODE

#include 
using namespace std;
const int N = 1010;
int n;
int h[N];
int f[N], g[N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> h[i];
	for (int i = 1; i <= n; i++)
	{
		f[i] = 1;
		for (int j = 1; j < i; j++)
			if (h[i] > h[j])f[i] = max(f[i], f[j] + 1);
	}
	for (int i = n; i >= 1; i--)
	{
		g[i] = 1;
		for (int j = n; j > i; j--)
			if (h[i] > h[j])g[i] = max(g[i], g[j] + 1);
	}
	int res = 0;
	for (int i = 1; i <= n; i++)
		res = max(res, f[i] + g[i] - 1);
	cout << res << endl;
	return 0;
}

482. 合唱队行

题目链接：合唱队行
题目描述
给定长度为n的数组a[n]，存同学的身高
要求我们删除一些小朋友，最终使得身高顺序先递增后递减,求最少删除多少小朋友
题目分析
删除最少的小朋友==求最长的先上升后下降的子序列，转换后和上题完全一直
CODE

#include 
using namespace std;
const int N = 1010;
int n;
int h[N];
int f[N], g[N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> h[i];
	for (int i = 1; i <= n; i++)
	{
		f[i] = 1;
		for (int j = 1; j < i; j++)
			if (h[i] > h[j])f[i] = max(f[i], f[j] + 1);
	}
	for (int i = n; i >= 1; i--)
	{
		g[i] = 1;
		for (int j = n; j > i; j--)
			if (h[i] > h[j])g[i] = max(g[i], g[j] + 1);
	}
	int res = 0;
	for (int i = 1; i <= n; i++)
		res = max(res, f[i] + g[i] - 1);
	cout << n-res << endl;
	return 0;
}

1012. 友好城市

题目链接友好城市
题目描述
每个桥有x1和x2，桥的上岸的一头x1，下岸的一头x2，求在不相交的前提下，尽可能造出更多的桥,求出最大的造桥数量
题目分析
图片参考：彩色铅笔%%

https://www.acwing.com/solution/content/51858/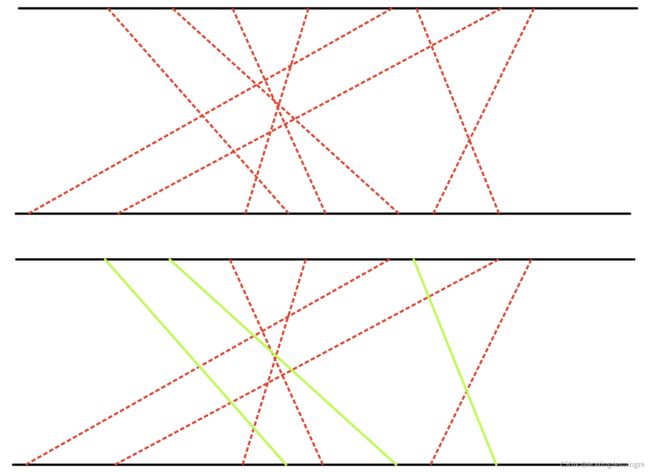
1 先将上坐标排序
2 找出下坐标的最长上升子序列

CODE

#include 
#define x first
#define y second
using namespace std;
typedef pair<int, int>PII;
const int N = 50010;
int n;
int f[N];
PII p[N];//存x1,x2
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> p[i].x >> p[i].y;
	sort(p + 1, p + n + 1);
	for (int i = 1; i <= n; i++)
	{
		f[i] = 1;
		for (int j = 1; j < i; j++)
			if (p[i].y > p[j].y)f[i] = max(f[i], f[j] + 1);
	}
	int res = 0;
	for (int i = 1; i <= n; i++)
		res = max(res, f[i]);
	cout << res << endl;
	return 0;
}

1016. 最大上升子序列和

题目链接最大上升子序列和
题目描述
满足从左到右数字递增的次序的子序列的和
求最大上升子序列和
题目分析
此题只需将最长上升子序列的个数换为元素和即可
CODE

#include 
using namespace std;
const int N = 1010;
int a[N], f[N], n;
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> a[i], f[i] = a[i];
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j < i; j++)
			if (a[i] > a[j])f[i] = max(f[i], f[j] + a[i]);
	}
	int res = 0;
	for (int i = 1; i <= n; i++)
		res = max(res, f[i]);
	cout << res << endl;
	return 0;
}

1010. 拦截导弹

题目链接拦截导弹
题目描述
导弹拦截系统只能拦截发射第一枚拦截导弹之下且不能再上升的导弹，求导弹系统数
题目分析
第一问求最长不上升子序列即可
第二问
贪心流程：
1 如果现有的子序列的结尾都小于当前数，则创建新子序列
2 将当前数梵高结尾大于等于它的最小的子序列后面
CODE

#include 
using namespace std;
const int N = 1010;
int a[N], g[N], f[N];
int res, cnt, n=1;
int main()
{
	while(cin>>a[n])n++;
	n--;
	for (int i = 1; i <= n; i++)
	{
		f[i] = 1;
		for (int j = 1; j < i; j++)
		{
			if (a[i] <= a[j])
				f[i] = max(f[i], f[j] + 1);
			res = max(res, f[i]);
		}
	}
	cout << res << endl;
	for (int i = 1; i <= n; i++)
	{
		int k = 0;
		while (k < cnt && g[k] < a[i])k++;
		g[k] = a[i];
		if (k >= cnt)cnt++;
	}
	cout << cnt << endl;
	return 0;
}

187. 导弹防御系统

题目链接：导弹防御系统
题目描述
给定元素w[i]应该被加到上升子序列还是下降子序列
题目分析
暴力dfs+剪枝
CODE

#include 
using namespace std;
const int N = 55;
int a[N], ans, up[N], down[N], n;
void dfs(int u,int d,int t)//上升系统个数，下降系统个数，当前第t个数
{
	if (u + d >= ans)return;//如果超过最有答案直接剪枝
	if (t == n)
	{
		if (u + d < ans)ans = u + d;
		return;
	}
	int i;
	//贪心
	for ( i = 1; i <= u; i++)
		if (up[i] < a[t])break;
	int temp = up[i];
	up[i] = a[t];
	dfs(max(u, i), d, t + 1);//新增系统or直接加入
	up[i] = temp;//恢复现场
	//同理
	for ( i = 1; i <= d; i++)
		if (down[i] > a[t])break;
	temp = down[i];
	down[i] = a[t];
	dfs(u, max(d, i), t + 1);
	down[i] = temp;
}
int main()
{
	while(scanf("%d", &n) != EOF && n != 0)
	{
		ans = 100;
		for (int i = 0; i < n; i++)
			cin >> a[i];
		dfs(0, 0, 0);
		printf("%d\n",ans);
	}
	return 0;
}

272. 最长公共上升子序列

题目链接：最长公共上升子序列
题目描述
给定两个长度为n的数组a[n],b[n]
求两个数组的最长公共上升子序列
题目分析
集合：f[i][j]：考虑a中的前i个数字，b中前j个数字，且当前一b[j]结尾的方案
属性：该方案的子序列最大长度max
状态转移：

1. 考虑a数组前i-1个数字，b数组中前j个数字，且以b[j]结尾的子序列的方案转移过来
2. 考虑a数组中前i个数字，b数组中前k个数字，且当前以b[k]结尾的子序列的方案中转移：
   
   
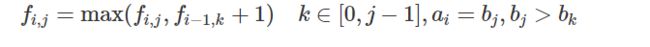
   朴素版会TLE 时间复杂度O(n^3)
   因此需采用优化
   CODE（朴素版本）

#include 
using namespace std;
const int N = 3010;
int n;
int a[N], b[N];
int f[N][N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> a[i];
	for (int i = 1; i <= n; i++)cin >> b[i];
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			f[i][j] = f[i - 1][j];
			if (a[i] == b[j])
			{
				for (int k = 0; k < j; k++)
				{
					if (b[j] > b[k])
						f[i][j] = max(f[i][j], f[i - 1][k] + 1);
				}
			}
		}
	}
	int res = 0;
	for (int i = 0; i <= n; i++)
		res = max(res, f[n][i]);
	cout << res << endl;
	return 0;
}

CODE（优化版）

#include 
using namespace std;
const int N = 3010;
int n;
int a[N], b[N];
int f[N][N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> a[i];
	for (int i = 1; i <= n; i++)cin >> b[i];
	for (int i = 1; i <= n; i++)
	{
		int maxv = 1;
		for (int j = 1; j <= n; j++)
		{
			f[i][j] = f[i - 1][j];
			if (a[i] == b[j])f[i][j] = max(f[i][j], maxv);
			if (b[j] < a[i])maxv = max(maxv, f[i - 1][j]+1);
		}
	}
	int res = 0;
	for (int i = 0; i <= n; i++)
		res = max(res, f[n][i]);
	cout << res << endl;
	return 0;
}

背包问题

423. 采药

题目链接：采药
题目描述
给定n株药和m个单位时间
给定每株药采集需要的时间v，以及价值w
求出一种方案在时间m内采药的最大价值
题目分析
时间—>体积
价值—>物品价值
背包问题
每株草药只有一个，因此是01背包问题
此题是模板题直接写代码即可
状态表示：f[i][j]，前 i 个物品，体积不超过 j
属性：最大价值max
不选第 i 个物品 f[i-1][j]
选第 i 个物品 f[i-1][j-v[i]]+w[i]
CODE（朴素版）

#include 
using namespace std;
const int N = 110, M = 1010;
int n, m;
int w[N], v[N];
int f[N][M];
int main()
{
	cin >> m >> n;
	for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			f[i][j] = f[i - 1][j];//初始化全部不选
			if (j >= v[i])f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
		}
	}
	cout << f[n][m] << endl;
	return 0;
}

CODE（一维优化）

因为每次更新f[i]，都用到了上一层f[i-1]，所以在一维状态时，必须使用逆序，画个图理解以下

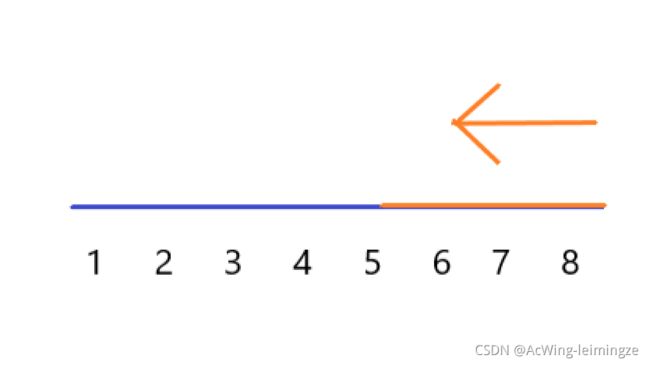
黄色是第 i 层更新的，蓝色是 i-1层更新的，如果正向更新，则 i-1 层会被 “污染”

#include 
using namespace std;
const int N = 110, M = 1010;
int n, m;
int w[N], v[N];
int f[M];
int main()
{
	cin >> m >> n;
	for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
	for (int i = 1; i <= n; i++)
		for (int j = m; j >= v[i]; j--)
			f[j] = max(f[j], f[j - v[i]] + w[i]);
	cout << f[m] << endl;
	return 0;
}

1024. 装箱问题

题目链接：装箱问题
题目描述
给定一个容量为 m 的箱子，以及 n 个物品
每个物品 i 有一个体积 vi要求我们找出一个装箱方案，使得箱子的剩余空间最少
题目分析
典型的01 背包的题目问题，没有给出物品的价值，在体积不超过容量的情况最大
物品的价值就是物品的体积
CODE

#include 
using namespace std;
const int N = 35, M = 20010;
int n, m;
int v[N];
int f[M];
int main()
{
	cin >> m >> n;
	for (int i = 1; i <= n; i++)cin >> v[i];
	for (int i = 1; i <= n; i++)
		for (int j = m; j >= v[i]; j--)
			f[j] = max(f[j], f[j - v[i]] + v[i]);
	cout << m - f[m] << endl;
	return 0;
}

1022. 宠物小精灵之收复

题目链接：宠物小精灵之收复
题目描述
大聪明和皮卡丘抓宝可梦
一共会遇到n个野生宝可梦，大聪明有 m 个 精灵球，皮卡丘有 t 滴血， 对于每个野生宝可梦来说，需要v1i个精灵球，皮卡丘会掉v2i滴血
皮卡丘血量小于等于 0 时，校址停止狩猎，小智对每个野生包可能妖魔收服要么逃跑
收复尽可能多的野生宝可梦，如果收服数量一样，要皮卡丘血量最多
请输出野生宝可梦收服数量，以及皮卡丘战斗结束后的剩余血量
题目分析
本题是一道二维费用 01 背包问题
把野生宝可梦看做物品，需要的精灵球个数就是第一维费用，战斗皮神要掉的血就是第二维费用

CODE

#include 
using namespace std;
const int N = 110, M = 1010, K = 510;
int n, m, t;
int v1[N], v2[N];
int f[M][K];
int main()
{
	cin >> m >> t >> n;
	for (int i = 1; i <= n; i++)cin >> v1[i] >> v2[i];
	for (int i = 1; i <= n; i++)
	{
		for (int j = m; j >= v1[i]; j--)
		{
			for (int k = t - 1; k >= v2[i]; k--)
				f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + 1);
		}
	}
	cout << f[m][t - 1] <<" ";
	int cost_health = t;
	for (int k = 0; k <= t - 1; k++)
	{
		if (f[m][k] == f[m][t - 1])
			cost_health = min(cost_health, k);
	}
	cout << t - cost_health << endl;
	return 0;
}

278. 数字组合

题目链接：数字组合
题目描述
给定n个整数：a1,a2,a3…an
求他们的方案数
题目分析
状态表示：f[i][j]在前 i 个中选，和恰好是 j 的方案数
属性：求方案数
CODE

#include 
using namespace std;
const int N = 110, M = 10010;
int n, m;
int v[N];
int f[M];
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> v[i];
	f[0] = 1;//j=0也是一种方案
	for (int i = 1; i <= n; i++)
		for (int j = m; j >= v[i]; j--)
			f[j] += f[j - v[i]];
	cout << f[m] << endl;
	return 0;
}

1023. 买书

题目链接：买书
题目描述
给定小明 n 元全部买书，书的价格为10，20，50，100
求小明有多少种买书方案，每一种书可以买多本
题目分析
由题意可知这是一道完全背包求方案数
状态表示：f[i][j]，前 i 个物品，价值为 j 的方案
属性：求方案数

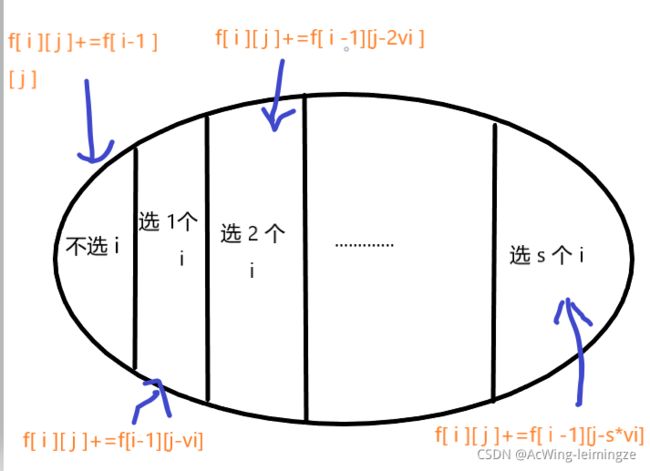
CODE（朴素版）

#include
using namespace std;
const int N = 5, M = 1010;
int n = 4, m;
int v[N] = { 0,10,20,50,100 };
int f[N][M];
int main()
{
	cin >> m;
	f[0][0] = 1;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j <= m; j++)
		{
			for (int k = 0; v[i] * k <= j; k++)
				f[i][j] += f[i - 1][j - k * v[i]];
		}
	}
	cout << f[n][m] << endl;
	return 0;
}

完全背包优化
f[i][j]=f[i-1][j]+f[i-1][j-vi]+f[i-1][j-2*vi]+......+f[i-1][j-s*vi]
f[i][j-vi]= f[i-1][j-vi]+f[i-1][j-2*vi]+......+f[i-1][j-s*vi]
因此 f[i][j]=f[i-1][j]+f[i][j-vi] 与k无关
CODE(二维优化)

#include 
using namespace std;
const int N = 5, M = 1010;
int n = 4, m;
int v[N] = { 0,10,20,50,100 };
int f[N][M];
int main()
{
	cin >> m;
	f[0][0] = 1;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j <= m; j++)
		{
		    f[i][j]+=f[i-1][j];
		    if(j>=v[i])
			f[i][j]+=f[i][j-v[i]];
		}
	}
	cout << f[n][m] << endl;
}

CODE(一维优化)

#include 
using namespace std;
const int N = 5, M = 1010;
int n = 4, m;
int v[N] = { 0,10,20,50,100 };
int f[M];
int main()
{
	cin >> m;
	f[0] = 1;
	for (int i = 1; i <= n; i++)
		for (int j = v[i]; j <= m; j++)
			f[j] += f[j - v[i]];
	cout << f[m] << endl;
}

1021. 货币系统(Ⅰ)
题目链接：货币系统
题目描述
给定一个 n 种面值的货币系统，求组成面值为 m 的货币系统有多少种方案。
题目分析
完全背包求方案数，与上题思路一致
此题需要开long long ，否则会爆 int
CODE

#include 
using namespace std;
typedef long long LL;
const int N = 20, M = 3010;
int n, m;
int v[N];
LL f[M];
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> v[i];
	f[0] = 1;
	for (int i = 1; i <= n; i++)
		for (int j = v[i]; j <= m; j++)
			f[j] += f[j - v[i]];
	cout << f[m] << endl;
	return 0;
}

货币系统（Ⅱ）

题目链接：货币系统
题目分析
此处参考彩色铅笔巨巨：https://www.acwing.com/solution/content/53198/
膜拜膜拜！！
定义一个货币系统（n , a）n种货币，面值为ai
k=x1a1+x2a2+…+xn*an
k为货币系统（n,a）能够线性表出的数值
(n , a)和(m , b)等价：k如果能被a线性表出，则也能被b表出，反之也成立
如果 aj 能被其他 a 中其他向量线性表出，则 aj 是无效的，因此我们需要求出最大无关向量组，即 ai 不能被其他向量表示
无效的 ai 总能被比他小的元素线性组合表出，因此我们需要先排序
由题意可知这是一道完全背包，需要稍作改动

CODE(二维)

#include 
using namespace std;
const int N = 110, M = 25010;
int a[N], f[N][M];
int t, n;
int main()
{
	cin >> t;
	while (t--)
	{
		cin >> n;
		for (int i = 1; i <= n; i++)cin >> a[i];
		sort(a + 1, a +n + 1);
		memset(f, 0, sizeof f);
		int ans = 0;
		for (int i = 1; i <= n; i++)
		{
			if (!f[i - 1][a[i]])ans++;
			for (int j = 1; j < M; j++)
			{
				f[i][j] = f[i - 1][j];
				if (j > a[i])f[i][j] |= f[i][j - a[i]];
				else if (j == a[i])f[i][j] = 1;
			}
		}
		cout << ans << endl;
	}
	return 0;
}

CODE(一维)

#include 
using namespace std;
const int N = 110, M = 25010;
int v[N], f[M];
int t, n;
int main()
{
	cin >> t;
	while (t--)
	{
		cin >> n;
		for (int i = 0; i < n; i++)cin >> v[i];
		sort(v , v + n);
		int res = 0;
		memset(f, 0, sizeof f);
		f[0] = true;
		for (int i = 0; i < n; i++)
		{
			if (!f[v[i]])res++;
			for (int j = v[i]; j <= v[n - 1]; j++)
			{
				f[j] += f[j - v[i]];
			}
		}
		cout << res << endl;
	}
	return 0;
}

1019. 庆功宴

题目链接：庆功宴
题目描述
n种奖品，m元现金，对于第 i 种奖品，价格为 vi 价值为wi ，数量为 si
指定一个购买方案，使得该方案的总价值最大
题目分析
初步判断此题为 多重背包问题
状态表示：f[i][j]在前 i 个物品中选，体积不超过j的方案的价值
属性：MAX
状态转移方程：f[i][j]=max(f[i][j],f[i-1][j-k*v]+k*w)

CODE(朴素写法)

#include 
using namespace std;
const int N = 510, M = 6010;
int n, m;
int v[N], w[N], s[N];
int f[N][M];
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> v[i] >> w[i]>> s[i];
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j <= m; j++)
		{
			for (int k = 0; k <= s[i]; k++)
			{
				if (j >= k * v[i])f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
			}
		}
	}
	cout << f[n][m] << endl;
	return 0;
}

CODE(一维优化)

#include 
using namespace std;
const int N = 510, M = 6010;
int n, m;
int v[N], w[N], s[N];
int f[M];
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> v[i] >> w[i] >> s[i];
	for (int i = 1; i <= n; i++)
		for (int j = m; j >= v[i]; j--)
			for (int k = 0; k <= s[i]; k++)
				if (k * v[i] <= j)f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
	cout<<f[m]<<endl;
	return 0;

}

7. 混合背包问题

题目链接：混合背包问题
题目描述
n 种物品和容量为** m **的背包
物品分为三类：

1. 第一类物品只能用** 1 次（01背包）**
2. 第二类物品可以用无限次**（完全背包）**
3. 第三类物品最多只能用si 次**(多重背包)**
   每种体积是 vi ,价值是 wi
   求体积不超过背包的容量且总价值最大
   题目分析
   这里主要说一下多重背包的二进制转化成01背包
   举个例子：
   我们将11拆成1，2，4，4，二进制分别为001，010，100，100，其中1，2，4可以组合成11内任何一个数。，我们只需要枚举四次
   01优化代码：

for (int k = 1; k <= s; k *= 2)
{
	s -= k;
	goods.push({ v * k,w * k });
}
if (s > 0)goods > push_bakc({ v * s,w * s });

完整版本二进制优化多重背包
题目链接：多重背包Ⅱ

#include 
using namespace std;
const int N=2010;
int f[N];
int v[N],w[N],s[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i]>>s[i];
    for(int i=1;i<=n;i++)
    {
        for(int k=1;k<=s[i];k*=2)
        {
            s[i]-=k;
            for(int j=m;j>=k*v[i];j--)
            f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);   
        }
        if(s[i])
        for(int j=m;j>=s[i]*v[i];j--)
        f[j]=max(f[j],f[j-s[i]*v[i]]+w[i]*s[i]);
    }
    cout<<f[m]<<endl;
    return 0;
    
}

CODE（一维优化）

#include 
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N], s[N];
int f[N];
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> v[i] >> w[i] >> s[i];
	for (int i = 1; i <= n; i++)
	{
		if (!s[i])//完全背包
		{
			for (int j = v[i]; j <= m; j++)
				f[j] = max(f[j], f[j - v[i]] + w[i]);
		}
		else
		{
			if (s[i] == -1)s[i] = 1;
			for (int k = 1; k <= s[i]; k *= 2)
			{
				s[i] -= k;
				for (int j = m; j >= k * v[i]; j--)
					f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
			}
			if (s[i])
			{
				for (int j = m; j >= s[i] * v[i]; j--)
					f[j] = max(f[j], f[j - s[i] * v[i]] + s[i] * w[i]);
			}
		}
	}
	cout << f[m] << endl;
	return 0;
}

8. 二维费用背包问题

题目链接：二维费用背包问题
题目描述

给 n 件物品 和一个容量 为 v 的背包，背包最大承重是M
每件物品只能用一次，第 i件物品的体积是vi，重量mi,价值是wi
求解一个选物品的 方案，使得 总体积 不超过** V**，总重量 不超过** M** 的，且 总价值 最大
题目分析

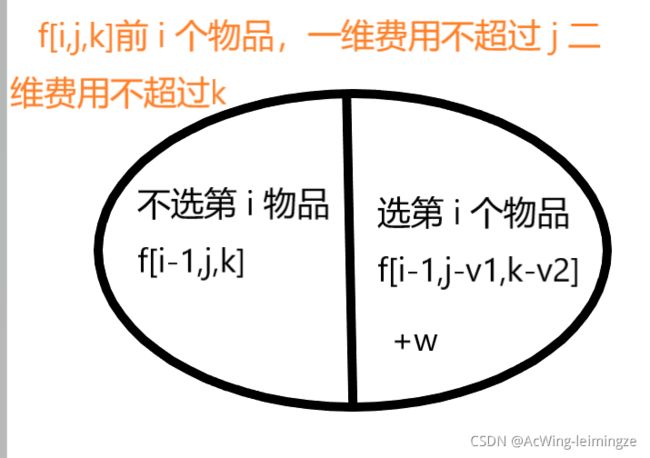
CODE(二维优化)

#include 
using namespace std;
const int N = 1010, K = 110;
int n, V, M;
int v1[N], v2[N], w[N];
int f[K][K];
int main()
{
	cin >> n >> V >> M;
	for (int i = 1; i <= n; i++)cin >> v1[i] >> v2[i] >> w[i];
	for (int i = 1; i <= n; i++)
		for (int j = V; j >= v1[i]; j--)
			for (int k = M; k >= v2[i]; k--)
				f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]]+w[i]);
	cout << f[V][M] << endl;
	return 0;
}

1020. 潜水员

题目链接：潜水员
题目描述
一共有 k 种物品，对于第 i 种物品，第一维费用是 v1i，第二维是费用是v2i，价值是wi
求一个选择方案，使得第一维费用不少于 n，第二维费用不少于 m,且总价值 最小。
题目分析
01背包二位费用不少于问题，
参考：https://www.acwing.com/solution/content/7438/

CODE

#include 
using namespace std;
const int N = 1010, M = 85;
int n, m, t;
int v1[N], v2[N], w[N];
int f[M][M];
int main()
{
	cin >> n >> m >> t;
	for (int i = 1; i <= t; i++)cin >> v1[i] >> v2[i] >> w[i];
	memset(f, 0x3f, sizeof f);
	f[0][0] = 0;
	for (int i = 1; i <= t; i++)
		for (int j = n; j >= 0; j--)
			for (int k = m; k >= 0; k--)
				f[j][k] = min(f[j][k], f[max(j - v1[i], 0)][max(k - v2[i], 0)]+w[i]);
	cout << f[n][m] << endl;
	return 0;
}

为什么这里需要枚举到0?

1013. 机器分配（分组背包）

题目链接：机器分配
题目描述
有M台机器，分配给N个公司，求最大利益
给定一个NxM的矩阵，第 i 行第 j 列表示第 i 个公司分配 j 台机器的盈利
题目分析
我们可以把每个公司堪称一个物品组，因此，对于分给第 i 个公司的不同机器数量可以看作是一个物品组里的物品
CODE（分组背包）

#include 
using namespace std;
const int N = 20;
int n, m;
int w[N][N];
int f[N][N];
int path[N];
int cnt;
void dfs(int i, int j)
{
	if (!i)return;
	for (int a = 0; a <= j; a++)
	{
		if (f[i - 1][j - a] + w[i][a] == f[i][j])
		{
			path[cnt++] = a;
			dfs(i - 1, j - a);
			return;
		}
	}
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			cin >> w[i][j];
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			for (int k = 0; k <= j; k++)
				f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
	cout << f[n][m] << endl;
	dfs(n, m);
	for (int i = cnt - 1, id = 1; i >= 0; i--, id++)
		cout << id << " " << path[i] << endl;
	return 0;
}

426. 开心的金明

题目链接：开心的金明
题目描述
给定N元，M件物品。
第 j 件物品的价格为 v[j]，重要度为 w[j]，共选中了 k 件物品，编号依次为 j1，j2，…，jk，则所求的总和为： 
v[j1]×w[j1]+v[j2]×w[j2]+…+v[jk]×w[jk]
题目分析
01背包问题
CODE

#include 
using namespace std;
const int N = 30, M = 30010;
int n, m;
int v[N], w[N];
int f[M];
int main()
{
	cin >> m >> n;
	for (int i = 1; i <= n; i++)cin >> v[i] >> w[i], w[i] *= v[i];
	for (int i = 1; i <= n; i++)
		for (int j = m; j >= v[i]; j--)
			f[j] = max(f[j], f[j - v[i]] + w[i]);
	cout << f[m] << endl;
	return 0;
}

10. 有依赖的背包问题

题目链接：有依赖的背包问题
题目描述

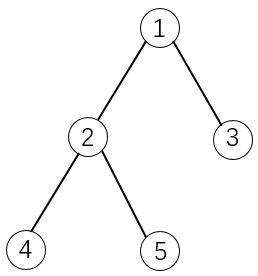
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
先枚举状态子节点，从下往上获得做大价值
CODE

#include 
using namespace std;
const int N = 110;
int n, m, root;
int h[N], e[N], ne[N], idx;
int v[N], w[N];
int f[N][N];
void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
void dfs(int u)
{
	for (int i = h[u]; ~i; i = ne[i])
	{
		int son = e[i];
		dfs(son);
		for (int j = m - v[u]; j >= 0; j--)
			for (int k = 0; k <= j; k++)
				f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
	}
	for (int j = m; j >= v[u]; j--)f[u][j] = f[u][j - v[u]] + w[u];
	for (int j = 0; j < v[u]; j++)f[u][j] = 0;
}
int main()
{
	memset(h, -1, sizeof h);
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		int p;
		cin >> v[i] >> w[i] >> p;
		if (p == -1)root = i;
		else add(p, i);
	}
	dfs(root);
	cout << f[root][m] << endl;
}

11. 背包问题求方案数

题目链接：背包问题求方案数
题目描述
01背包求方案数，模1e9+7
题目分析
模板
CODE

#include 
using namespace std;
const int N = 1010;
const int MOD = 1e9 + 7;
int n, m;
int w[N], v[N];
int f[N][N], g[N][N];
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j <= m; j++)
		{
			f[i][j] = f[i - 1][j];
			if (j >= v[i])f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
		}
	}
	g[0][0] = 1;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j <= m; j++)
		{
			if (f[i][j] == f[i - 1][j])
				g[i][j] = g[i - 1][j] % MOD;
			if (j >= v[i] && f[i][j] == f[i - 1][j - v[i]] + w[i])
				g[i][j] = (g[i][j] + g[i - 1][j - v[i]]) % MOD;
		}
	}
	int res = 0;
	for (int j = 0; j <= m; j++)
		if (f[n][j] == f[n][m])
			res = (res + g[n][j]) % MOD;
	cout << res << endl;
	return 0;
}

12. 背包问题求具体方案

题目链接：背包问题求具体方案

参考：https://www.acwing.com/solution/content/7456/
CODE

#include 
using namespace std;
const int N = 1010;
int n, m;
int w[N], v[N];
int f[N][N];
int path[N], cnt;
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
	for (int i = n; i >= 1; i--)
	{
		for (int j = 0; j <= m; j++)
		{
			f[i][j] = f[i + 1][j];
			if (j >= v[i])f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
		}
	}
	for (int i = 1, j = m; i <= n; i++)
	{
		if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
		{
			path[cnt++] = i;
			j -= v[i];
		}
	}
	for (int i = 0; i < cnt; i++)cout << path[i] << " ";
	return 0;
}

734. 能量石

题目链接：能量石
题目描述
有N个石头，
对于每个石头，吃掉的时间是si，价值是wi，每单位时间的损耗是li
规定该石头刚开始吃时，该石头能量就不会损失了，求一种方案，总价值最大
题目分析
此题 贪心+01背包（恰好）
对于第 i块和第 i + 1石头，
先吃 i的能吃到能力为 e(i)+e(i+1)-s(i) x l(i+1)
后吃 i + 1 e(i)+e(i+1)s(i+1)xl(i)
当s(i)xl(i+1)i+1
前i个能量石中取，经过了恰好 j 时刻的解，所以只要找出 j 最大可能是多少就可以了，就是所有能量石时间总和sum
令f[i][j]为从前i个能量石中取，经过了恰好 j 时刻的解
f[i][j] = max(f[i][j],f[i-1][j-s]+max(0,e-l*(j - s)));

CODE

#include 
using namespace std;
const int N = 110, M = 1e5 + 10;
int n, m;
struct node
{
	int s, e, l;
	bool operator<(const node& t)const
	{
		return s * t.l < t.s* l;
	}
}a[N];
int f[M];
void solve()
{
	memset(f, -0x3f, sizeof f);
	f[0] = m = 0;
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> a[i].s >> a[i].e >> a[i].l, m += a[i].s;
	sort(a + 1, a + 1 + n);
	for (int i = 1; i <= n; i++)
	{
		for (int j = m; j >= a[i].s; j--)
		{
			int pre = j - a[i].s;
			f[j] = max(f[j], f[pre] + a[i].e - pre * a[i].l);
		}
	}
	int res = 0;
	for (int j = 0; j <= m; j++)res = max(res, f[j]);
	cout << res << endl;
}
int main()
{
	int t;
	cin >> t;
	int T = 1;
	while (t--)
	{
		cout << "Case #" << T++ << ": ";
		solve();
	}
	return 0;
}

487. 金明的预算方案

题目链接：金明的预算方案
题目描述
一共有N个物品和M元钱，物品之间可能存在依赖关系，对于第i 个物品，价格为vi，价值为wi，依赖的父物品为pi；
每个物品只能被购买一次
依赖关系：只有购买了父物品后，才能购买子物品（若pi = 0 表示该物品的主件）
求一种购买方案，使得总花费不超过M，其总价值最大
题目分析

有依赖的背包DP

参考：https://www.acwing.com/solution/content/3803/

#include 
#define v first
#define w second
using namespace std;
const int N = 60, M = 32010;
typedef pair<int, int>PII;
int n, m;
PII master[N];
vector<PII>servent[N];
int f[M];
int main()
{
	cin >> m >> n;
	for (int i = 1; i <= n; i++)
	{
		int v, p, q;
		cin >> v >> p >> q;
		p *= v;
		if (!q)master[i] = { v,p };//主件
		else servent[q].push_back({ v,p });
	}
	for (int i = 1; i <= n; i++)
	{
		for (int u = m; u >= 0; u--)
		{
			for (int j = 0; j < 1 << servent[i].size(); j++)
			{
				int v = master[i].v, w = master[i].w;
				for (int k = 0; k < servent[i].size(); k++)
				{
					if (j >> k & 1)
					{
						v += servent[i][k].v;
						w += servent[i][k].w;
					}
				}
				if (u >= v)f[u] = max(f[u], f[u - v] + w);
			}
		}
	}
	cout << f[m] << endl;
	return 0;
}

状态机模型

1049. 大盗阿福

题目链接：大盗阿福
题目描述
阿福打算洗劫一条街的店铺，不能同时洗劫两家相邻的，求可获取最大价值
题目分析
这是一道状态机模板题
状态表示 f[i][j] ：
考虑前 i 家店铺，第 i 家店铺偷 1，不偷 0
属性：求最大价值MAX
状态转移方程:
f[i][0]=max(f[i-1][1],f[i-1][0])
f[i][1]=f[i-1]+w[i]

#include 
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n;
int t;
int w[N];
int f[N][2];
int main()
{
	cin >> t;
	while (t--)
	{
		cin >> n;
		for (int i = 1; i <= n; i++)cin >> w[i];
		for(int i=1;i<=n;i++)
		{
			f[i][0] = max(f[i - 1][0], f[i - 1][1]);
			f[i][1] =f[i - 1][0] + w[i];
		}
		cout << max(f[n][0], f[n][1])<<endl;
	}
	return 0;
}

1057. 股票购买Ⅳ

题目链接：股票购买Ⅳ
题目描述
给定一个长度为 N 的数组，数组中的第 i 个数字表示一个给定股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润，你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。
题目分析
状态机模型
状态表示：f[i][j][m]考虑前 i 天，交易了 j 次，当前状态为 m
m==0 or m ==1 0表示空仓，1表示持仓
属性：最大价值MAX
状态转移方程：
f[i][j][0] = max(f[i-1][j][0],f[i-1][j][1] + w[i])
f[i][j][1] = max(f[i-1][j][1],f[i-1][j-1][0] - w[i])
CODE

#include 
using namespace std;
const int N = 1e5 + 10;
const int M = 110;
int w[N];
int f[N][M][2];
int n, k;
int main()
{
	cin >> n >> k;
	for (int i = 1; i <= n; i++)cin >> w[i];
	memset(f, -0x3f, sizeof f);
	for(int i = 0; i <= n; i++)f[i][0][0] = 0;
	for(int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= k; j++)
		{
			f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + w[i]);
			f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);
		}
	}
	int res = 0;
	for (int i = 0; i <= k; i++)
		res = max(res, f[n][i][0]);
	cout << res << endl;
	return 0;
}

1058. 股票买卖 V

题目链接：股票买卖Ⅴ
题目描述
给定一个长度为 N 的数组，数组中的第 i 个数字表示一个给定股票在第 i 天的价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
题目分析
遇上题分析类似
CODE（朴素）

#include 
using namespace std;
const int N = 100010;
int w[N];
int f[N][3];
int n;
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> w[i];
	memset(f, -0x3f, sizeof f);
	f[0][0] = 0;
	for (int i = 1; i <= n; i++)
	{
		f[i][0] = max(f[i - 1][0], f[i - 1][2]);
		f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
		f[i][2] = f[i - 1][1] + w[i];
	}
	cout << max(f[n][0], f[n][2]) << endl;
	return 0;
}

CODE(滚动数组)

#include 
using namespace std;
const int N = 1e5 + 10;
int w[N];
int f[2][3];
int n;
int main()
{
	//0 空仓，1，持仓 2，冷冻期
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> w[i];
	memset(f, -0x3f, sizeof f);
	f[0][0] = 0;
	for (int i = 1; i <= n; i++)
	{
		f[i & 1][0] = max(f[(i - 1) & 1][2], f[(i - 1) & 1][0]);
		f[i & 1][1] = max(f[(i - 1) & 1][1], f[(i - 1) & 1][0] - w[i]);
		f[i & 1][2] = f[(i - 1) & 1][1] + w[i];
	}
	cout << max(f[n & 1][0], f[n & 1][2]) << endl;
	return 0;
}

状态压缩DP

1064. 小国王

题目链接：小国王
题目描述
在 n×n 的棋盘上放 k 个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。
题目分析
压状DP模板题
枚举所有状态，筛选
状态表示：
f[i][j][k]前 i 成，已经选了 j 个，第 i 层状态为 k
状态属性 方案数
参考：https://www.acwing.com/solution/content/56348/

CODE

#include 
using namespace std;
typedef long long LL;
const int N = 12;
const int M = 1 << 10, K = 110;
int n, m;
vector<int>state;
int id[M];
vector<int>head[M];
int cnt[M];
LL f[N][K][M];
bool check(int state)
{
	for (int i = 0; i < n; i++)
	{
		if ((state >> i & 1) && (state >> i + 1 & 1))
			return false;
	}
	return true;
}
int count(int state)
{
	int res = 0;
	for (int i = 0; i < n; i++)
		if (state >> i & 1)res++;
	return res;
}
int main()
{
	cin >> n >> m;
	//预处理
	for (int i = 0; i < 1 << n; i++)
	{
		if (check(i))
		{
			state.push_back(i);
			id[i] = state.size() - 1;
			cnt[i] = count(i);
		}
	}
	f[0][0][0] = 1;
	//暴力枚举
	for (int i = 0; i < state.size(); i++)
	{
		for (int j = 0; j < state.size(); j++)
		{
			int a = state[i], b = state[j];
			if ((a & b) == 0 && check(a | b))
				head[i].push_back(j);
		}
	}
	f[0][0][0] = 1;
	for(int i = 1; i <= n + 1; i++)
		for(int j = 0 ; j <= m; j++)
			for(int a = 0; a < state.size(); a++)
				for (int b : head[a])
				{
					int c = cnt[state[a]];
					if (j >= c)
					{
						f[i][j][a] += f[i - 1][j - c][b];
					}
				}
	cout << f[n + 1][m][0] << endl;
	return 0;
}

327. 玉米田

题目链接：玉米田
思路与上题一致
这里用 0 表示合法， 1 表示不合法

#include 
using namespace std;
const int N = 14, M = 1 << 12, mod = 1e8;
int n, m;
int w[N];
vector<int>state;
vector<int>head[M];
int f[N][M];
bool check(int state)
{
	return !(state & (state << 1));
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		for (int j = 0; j < m; j++)
		{
			int t;
			cin >> t;
			w[i] += !t * (1 << j);
		}
	for (int i = 0; i < 1 << m; i++)
		if (check(i))state.push_back(i);
	for (int i = 0; i < state.size(); i++)
	{
		for (int j = 0; j < state.size(); j++)
		{
			int a = state[i], b = state[j];
			if (!(a & b))
				head[i].push_back(j);
		}
	}
	f[0][0] = 1;
	for (int i = 1; i <= n + 1; i++)
	{
		for (int j = 0; j < state.size(); j++)
			if (!(state[j] & w[i]))
				for (int k : head[j])
					f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
	}
	cout << f[n + 1][0] << endl;
	return 0;
}

292. 炮兵阵地

题目链接：炮兵阵地

思路一致

#include 
using namespace std;
const int N = 10, M = 1 << 10;
int n, m;
int g[1010];
int f[2][M][M];
vector<int>state;
int cnt[M];
bool check(int state)
{
	for (int i = 0; i < m; i++)
	{
		if ((state >> i & 1) && ((state >> i + 1 & 1) || (state >> i + 2 & 1)))
			return false;
	}
	return true;
}
int count(int state)
{
	int res = 0;
	for (int i = 0; i < m; i++)
		if (state >> i & 1)
			res++;
	return res;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j < m; j++)
		{
			char c;
			cin >> c;
			g[i] += (c == 'H')<<j;//山地
		}
	}
	for (int i = 0; i < 1<<m; i++)
	{
		if (check(i))
		{
			state.push_back(i);//筛选
			cnt[i] = count(i);//1的个数
		}
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j < state.size(); j++)//当前
		{
			for (int k = 0; k < state.size(); k++)//i-1
			{
				for (int u = 0; u < state.size(); u++)//i-2
				{
					int a = state[j];
					int b = state[k];
					int c = state[u];
					if (a & b | a & c | b & c)continue;
					if (g[i] & a | g[i - 1] & b)continue;
					f[i & 1][j][k] = max(f[i & 1][j][k], f[i - 1 & 1][k][u] + cnt[a]);
				}
			}
		}
	}
	int res = 0;
	for (int i = 0; i < state.size(); i++)
	{
		for (int j = 0; j < state.size(); j++)
		{
			res = max(res, f[n & 1][i][j]);
		}
	}
	cout << res << endl;
	return 0;
}

区间DP

1068. 环形石子合并

题目链接：环形石子合并
题目描述
给定 n 堆石子绕原型曹彰排放，将石子有序的合成一堆，规定只能选相邻的两堆，将新的一堆石子记作合并得分
选择一种合并石子的方案，使得做 n−1 次合并得分总和最大。
选择一种合并石子的方案，使得做 n−1 次合并得分总和最小。
题目分析
合并必须是相邻的两堆石子，所以此题不是哈夫曼树
所以此题考虑区间DP。
从 len = 1 开始枚举， ** len = n ** 是终态，
状态表示：f[len][i][j]当前合并的石子堆大小为 len ，且石子堆左端点 i ，右端点 j
状态属性 ：费用最大/最小
l + len - 1 = r，所以可以优化为二维
CODE

#include 
using namespace std;
const int N = 410, INF = 0x3f3f3f3f;
int n;
int w[N], s[N];
int f[N][N];
int g[N][N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> w[i], w[n + i] = w[i];
	for (int i = 1; i <= n * 2; i++)s[i] = s[i - 1] + w[i];
	memset(f, 0x3f, sizeof f);
	memset(g, -0x3f, sizeof g);
	for (int len = 1; len <= n; len++)
	{
		for (int l = 1; l + len - 1 <= n << 1; l++)
		{
			int r = l + len - 1;
			if (l == r)f[l][r] = g[l][r] = 0;
			else
			{
				for (int k = l; k + 1 <= r; k++)
				{
					f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
					g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
				}
			}
		}
	}
	int minv = INF, maxv = -INF;
	for (int i = 1; i <= n; i++)
	{
		minv = min(minv, f[i][i + n - 1]);
		maxv = max(maxv, g[i][i + n - 1]);
	}
	cout << minv << endl << maxv << endl;
	return 0;
}

320. 能量项链

题目链接：能量项链
题目描述
每个能量是有一个属性(wi1,wi2)

求产生能量最大值
题目分析
区间DP，本题输入为

以往 区间分割为[ l ][ k ],[ k + 1][ r ]
此题分割为 [ l ][ k ],[ k ][ r ]
k要共同来使用
为什么len 可以取到n+1呢？
ab bc cd de :abcde
ab bc cd :abcd
CODE(n+1)

#include 
using namespace std;
const int N = 210;
int n;
int w[N];
int f[N][N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> w[i], w[n + i] = w[i];
	for (int len = 3; len <= n + 1; len++)
	{
		for (int l = 1; l + len - 1 <= n << 1; l++)
		{
			int r = l + len - 1;
			for (int k = l + 1; k < r; k++)
			{
				f[l][r] = max(f[l][r], f[l][k] + f[k][r] + w[l] * w[k] * w[r]);
			}
		}
	}
	int res = 0;
	for (int i = 1; i <= n; i++)
		res = max(res, f[i][i + n]);
	cout << res << endl;
	return 0;
}

479. 加分二叉树

题目链接：加分二叉树
思路与上一致
CODE

#include 
using namespace std;
const int N = 50;
typedef pair<int, int>PII;
unsigned f[N][N];
int root[N][N];
int n;
int w[N];
void dfs(int l, int r)
{
	if (l > r)return;
	int k = root[l][r];
	cout << k << ' ';
	dfs(l, k - 1);
	dfs(k + 1, r);
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> w[i];
	for (int len = 1; len <= n; len++)
	{
		for (int l = 1; l + len - 1 <= n; l++)
		{
			int r = l + len - 1;
			for (int k = l; k <= r; k++)
			{
				int left = k == l ? 1 : f[l][k - 1];
				int right = k == r ? 1 : f[k + 1][r];
				int score = left * right + w[k];
				if (l == r)score = w[k];
				if (f[l][r] < score)
				{
					f[l][r] = score;
					root[l][r] = k;
				}
			}
		}
	}
	cout << f[1][n] << endl;
	dfs(1, n);
	return 0;
}

1069. 凸多边形的划分

题目链接：凸多边形的划分
题目描述

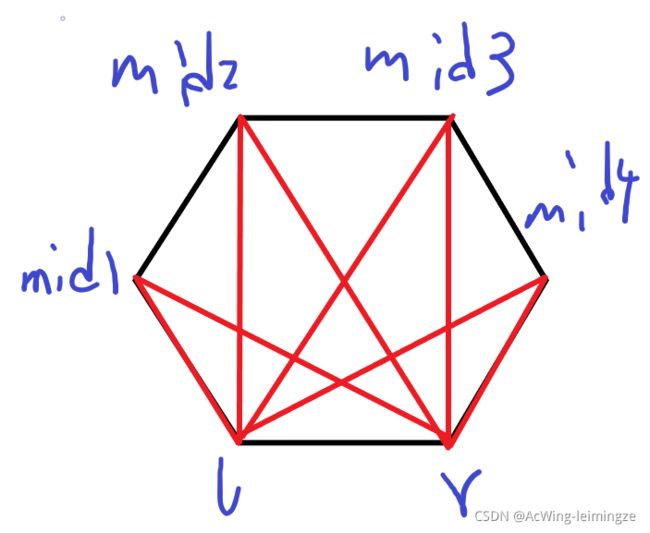
把多边形划分成n-2个三角形
求每次划分三角形费用的三个顶点的权值乘积
求方案费用综合最小
题目分析
集合：当前划分到多边形的左端点是 l ，右端点是 r
属性：费用最小
状态计算：
f[l][r]=min(f[l][k]+f[k][r]+wl*wk*wr)
CODE

#include 
using namespace std;
const int N = 55;
typedef long long LL;
int n;
int w[N];
vector<int>f[N][N];
bool cmp(vector<int>& a, vector<int>& b)
{
	if (a.size() != b.size())return a.size() < b.size();
	for (int i = a.size() - 1; i >= 0; i--)
		if (a[i] != b[i])return a[i] < b[i];
	return true;
}
vector<int>add(vector<int>a, vector<int>b)
{
	vector<int>c;
	int t = 0;
	for (int i = 0; i < a.size() || i < b.size(); i++)
	{
		if (i < a.size())t += a[i];
		if (i < b.size())t += b[i];
		c.push_back(t % 10);
		t /= 10;
	}
	while (t)
	{
		c.push_back(t % 10);
		t /= 10;
	}
	return c;
}
vector<int>mul(vector<int>a, LL b)
{
	vector<int>c;
	LL t = 0;
	for (int i = 0; i < a.size(); i++)
	{
		t += a[i] * b;
		c.push_back(t % 10);
		t /= 10;
	}
	while (t)
	{
		c.push_back(t % 10);
		t /= 10;
	}
	return c;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> w[i];
	for (int len = 3; len <= n; len++)
	{
		for (int l = 1; l + len - 1 <= n; l++)
		{
			int r = l + len - 1;
			for (int k = l + 1; k + 1 <= r; k++)
			{
				auto val = mul(mul({ w[l] },w[k]), w[r]);
				val = add(add(val, f[l][k]), f[k][r]);
				if (f[l][r].empty() || cmp(val, f[l][r]))f[l][r] = val;
			}
		}
	}
	auto res = f[1][n];
	for (int i = res.size() - 1; i >= 0; i--)
		cout << res[i];
	cout << endl;
	return 0;
}

树形DP

1072.树的最长路径

题目链接：树的最长路径
题目描述
给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

现在请你找到树中的一条最长路径。

换句话说，要找到一条路径，使得使得路径两端的点的距离最远。
题目分析

状态表示：
f1：以节点 i为根的子树中，从子树某个节点到 i 的最长路
f2以节点 i 为根的子树中，从子树某个节点到 i 的次长路
属性
最长路径MAX
状态转移：
CODE

#include 
using namespace std;
const int N = 1e4 + 10, M = N << 1;
int h[N], e[M], ne[M], w[M], idx;
int n;
int f1[N], f2[N], res;
void add(int a, int b, int c)
{
	e[idx] = b;
	ne[idx] = h[a];
	w[idx] = c;
	h[a] = idx++;
}
void dfs(int u, int father)
{
	for (int i = h[u]; ~i; i = ne[i])
	{
		int j = e[i];
		if (j == father)continue;
		dfs(j, u);
		if (f1[j] + w[i] > f1[u])f2[u] = f1[u], f1[u] = f1[j] + w[i];
		else if (f1[j] + w[i] > f2[u])f2[u] = f1[j] + w[i];
	}
	res = max(res, f1[u] + f2[u]);
}
int main()
{
	cin >> n;
	memset(h, -1, sizeof h);
	for (int i = 0; i < n - 1; i++)
	{
		int a, b, c;
		cin >> a >> b >> c;
		add(a, b, c);
		add(b, a, c);
	}
	dfs(1, -1);
	cout << res << endl;
	return 0;
}

1073. 树的中心

题目链接：树的中心
题目描述
给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。
题目分析
从当前节点往下，直到子树中某个节点的最长路径
从当前节点往上走到其父节点，再从其父节点出发且不回到该节点的最长路径

#include 
using namespace std;
const int N = 1e5 + 10, M = N << 1, INF = 0x3f3f3f3f;
int d1[N], d2[N], up[N], p1[N], p2[N];
int h[N], e[M], ne[M], w[M], idx;
int n;
void add(int a, int b, int c)
{
	e[idx] = b;
	w[idx] = c;
	ne[idx] = h[a];
	h[a] = idx++;
}
int dfs_down(int u, int father)
{
	for (int i = h[u]; ~i; i = ne[i])
	{
		int j = e[i];
		if (j == father)continue;
		int dist = dfs_down(j, u) + w[i];
		if (dist > d1[u])
		{
			d2[u] = d1[u];
			d1[u] = dist;
			p2[u] = p1[u];
			p1[u] = j;
		}
		else if (dist > d2[u])
		{
			d2[u] = dist;
			p2[u] = j;
		}
	}
	return d1[u];
}
void dfs_up(int u, int father)
{
	for (int i = h[u]; ~i; i = ne[i])
	{
		int j = e[i];
		if (j == father)continue;
		if (p1[u] == j)up[j] = max(up[u], d2[u]) + w[i];
		else  up[j] = max(up[u], d1[u]) + w[i];
		dfs_up(j, u);
	}
}
int main()
{
	cin >> n;
	memset(h, -1, sizeof h);
	for (int i = 0; i < n - 1; i++)
	{
		int a, b, c;
		cin >> a >> b >> c;
		add(a, b, c);
		add(b, a, c);
	}
	dfs_down(1, -1);
	dfs_up(1, -1);
	int res = INF;
	for (int i = 1; i <= n; i++)res = min(res, max(up[i], d1[i]));
	cout << res << endl;
	return 0;
}

1075. 数字转换

题目连接：数字转换
题目描述
如果一个数 x 的约数之和 y（不包括他本身）比他本身小，那么 x 可以变成 y，y 也可以变成 x。

例如，4 可以变为 3，1 可以变为 7。

限定所有数字变换在不超过 n 的正整数范围内进行，求不断进行数字变换且不出现重复数字的最多变换步数。
题目分析
参考：https://www.acwing.com/solution/content/65467/

#include 
using namespace std;
const int N = 50010, M = N;
int n;
int h[N], ne[M], e[M], idx;
int sum[M];
bool st[N];
int ans;
void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
int dfs(int u)
{
	st[u] = true;
	int dist = 0;
	int d1 = 0, d2 = 0;
	for (int i = h[u]; ~i; i = ne[i])
	{
		int j = e[i];
		if (!st[j])
		{
			int d = dfs(j) + 1;
			dist = max(d, dist);
			if (d > d1)d2 = d1, d1 = d;
			else if (d > d2)d2 = d;
		}
	}
	ans = max(ans, d1 + d2);
	return dist;
}
int main()
{
	cin >> n;
	memset(h, -1, sizeof h);
	for (int i = 1; i <= n; i++)
	{
		for (int j = 2; j <= n / i; j++)
			sum[i * j] += i;
	}
	for (int i = 2; i <= n; i++)
		if (sum[i] < i)
			add(sum[i], i);
	for(int i=1;i<=n;i++)
		if (!st[i])
			dfs(i);
	cout << ans << endl;
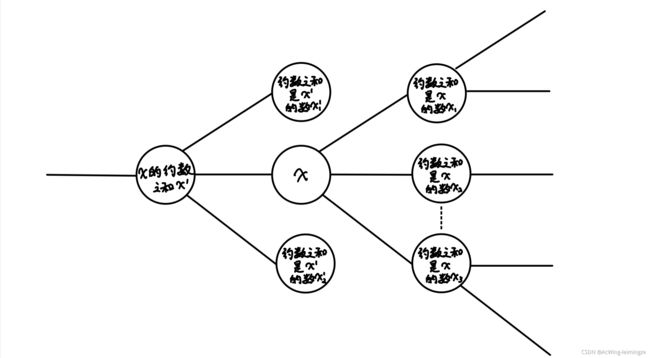
	return 0;
}

1074. 二叉苹果树

题目连接：二叉苹果树
题目描述
有一棵二叉苹果树，如果树枝有分叉，一定是分两叉，即没有只有一个儿子的节点。

这棵树共 N 个节点，编号为 1 至 N，树根编号一定为 1。

我们用一根树枝两端连接的节点编号描述一根树枝的位置。

一棵苹果树的树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。

题目分析
状态表示：
f[i][j]以 i 为根结点的子树，包含 i 的连通块的边数不超过 j 方案。
属性：f[i][j]的最大MAX
状态转移方程
f[i][j]=max(f[i][j-1-k]+f[son][k]+w[i],f[i][j])
CODE

#include 
using namespace std;
const int N = 110, M = N << 1;
int n, m;
int h[N], e[M], ne[M], w[M], idx;
int f[N][N];
void add(int a, int b, int c)
{
	e[idx] = b;
	w[idx] = c;
	ne[idx] = h[a];
	h[a] = idx++;
}
void dfs(int u, int father)
{
	for (int i = h[u]; ~i; i = ne[i])
	{
		int ver = e[i];
		if (ver == father)continue;
		dfs(ver, u);
		for (int j = m; j >= 0;j--)
		{
			for (int k = 0; k <= j - 1; k++)
				f[u][j] = max(f[u][j], f[u][j - k - 1] + f[ver][k] + w[i]);
		}
	}
}
int main()
{
	memset(h, -1, sizeof h);
	cin >> n >> m;
	for (int i = 0; i < n - 1; i++)
	{
		int a, b, c;
		cin >> a >> b >> c;
		add(a, b, c);
		add(b, a, c);
	}
	dfs(1, -1);
	cout << f[1][m] << endl;
	return 0;
}

323. 战略游戏

题目链接：战略游戏
题目描述

一个点与之相邻的点会被士兵观察到，求最少需要多少士兵。
题目分析
先递归到根节点，从下往上一次更新，不难，具体看代码实现
f[i][0] 表示i这个点不放置
f[i][1] 表示i这个点放置
代码核心

CODE

#include 
using namespace std;
const int N = 1510;
int n;
int f[N][2];
int h[N], e[N], ne[N], idx;
bool st[N];
void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
void dfs(int u, int father)
{
	f[u][0] = 0, f[u][1] = 1;
	for (int i = h[u]; ~i; i = ne[i])
	{
		int j = e[i];
		if (j == father)continue;
		dfs(j, u);
		f[u][0] += f[j][1];
		f[u][1] += min(f[j][1], f[j][0]);
	}
}
int main()
{
	while (cin >> n)
	{
		memset(h, -1, sizeof h);
		idx = 0;
		memset(st, 0, sizeof st);
		for (int i = 0; i < n; i++)
		{
			int id, cnt;
			scanf("%d:(%d)", &id, &cnt);
			while (cnt--)
			{
				int ver;
				cin >> ver;
				add(id, ver);
				st[ver] = true;
			}
		}
		int root = 0;
		while (st[root])root++;
		dfs(root, -1);
		printf("%d\n", min(f[root][1], f[root][0]));
	}
	return 0;
}

数位DP

1081. 度的数量

题目链接：度的数量
题目描述
求给定区间 [X,Y] 中满足下列条件的整数个数：这个数恰好等于 K 个互不相等的 B 的整数次幂之和。

例如，设 X=15,Y=20,K=2,B=2，则有且仅有下列三个数满足题意：

17=24+20
18=24+21
20=24+22
题目分析

代码参考y总
CODE

#include 
using namespace std;
const int N = 35;
int f[N][N];
int K, B;
void init()
{
	for (int i = 0; i < N; i++)
		for (int j = 0; j <= i; j++)
			if (!j)f[i][j] = 1;
			else f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
}
int dp(int n)
{
	if (n == 0)return 0;
	vector<int>nums;
	while (n)nums.push_back(n % B), n /= B;
	int res = 0;
	int last = 0;
	for (int i = nums.size() - 1; i >= 0; i--)
	{
		int x = nums[i];
		if (x > 0)//只有x>0时才能左右分支
		{
			res += f[i][K - last];//左分支，预处理所有填0
			if (x > 1)
			{
				if (K - last - 1 >= 0)res += f[i][K - last - 1];
				break;
			}
			else//x==1的情况，即右分支的一种情况
			{
				last++;
				if (last > K) break;
			}
		}
		if (i == 0 && last == K)res++;
	}
	return res;
}
int main()
{
	init();
	int l, r;
	cin >> l >> r >> K >> B;
	cout << dp(r) - dp(l - 1) << endl;
	return 0;
}

1082. 数字游戏

题目链接：数字游戏
题目描述
求一个区间没不下降数的个数
题目分析
占坑后填
CODE

#include 
using namespace std;
const int N = 15;
int f[N][N];//前 i 位,最高位为 j 
void init()
{
	for (int i = 0; i <= 9; i++)f[1][i] = 1;
	for (int i = 2; i < N; i++)
		for (int j = 0; j <= 9; j++)
			for (int k = j; k <= 9; k++)
				f[i][j] += f[i - 1][k];
}
int dp(int n)
{
	if (!n)return 1;
	vector<int>nums;
	while (n)nums.push_back(n % 10), n /= 10;
	int res = 0;
	int last = 0;
	for (int i = nums.size() - 1; i >= 0; i--)
	{
		int x = nums[i];
		for (int j = last; j < x; j++)//左支
			res += f[i + 1][j];
		if (last > x)break;
		last = x;
		if (!i)res++;
	}
	return res;
}
int main()
{
	init();
	int l, r;
	while (cin >> l >> r)cout << dp(r) - dp(l - 1) << endl;
	return 0;
}

1083. Windy数

题目链接：Windy数
题目描述
不含前导零且相邻两个数字之差至少为 2 的正整数被称为 Windy 数。
求一个区间内的Windy数

#include 
using namespace std;
const int N = 11;
int f[N][10];//前i位最高位j
void init()
{
	for (int i = 0; i <= 9; i++)f[1][i] = 1;
	for (int i = 2; i < N; i++)
		for (int j = 0; j <= 9; j++)
			for (int k = 0; k <= 9; k++)
				if (abs(j - k) >= 2)
					f[i][j] += f[i - 1][k];
}
int dp(int n)
{
	if (!n)return 0;
	vector<int>nums;
	while (n)nums.push_back(n % 10), n /= 10;
	int res = 0;
	int last = -2;
	for (int i = nums.size() - 1; i >= 0; i--)
	{
		int x = nums[i];
		for (int j = i == nums.size() - 1; j < x; j++)
		{
			if (abs(j - last) >= 2)
				res += f[i + 1][j];
		}
		if (abs(x - last) >= 2)last = x;
		else break;
		if (!i)res++;
	}
	//处理前导0
	for (int i = 1; i < nums.size(); i++)
		for (int j = 1; j <= 9; j++)
			res += f[i][j];
	return res;
}
int main()
{
	init();
	int l, r;
	cin >> l >> r;
	cout << dp(r) - dp(l - 1) << endl;
	return 0;
}