HashMap底层数据结构详解

一、HashMap底层数据结构

• JDK1.7及之前：数组+链表
• JDK1.8：数组+链表+红黑树

关于HashMap基本的大家都知道，但是为什么数组的长度必须是2的指数次幂，为什么HashMap的加载因子要设置为0.75，为什么链表长度大于等于8时转成了红黑树？

HashMap添加元素分析

当添加元素时，会通过哈希值和数组长度计算计算下标来准确定位该元素应该put的位置，通常我们为了使元素时分布均匀会使用取模运算，用一个值去模上总长度，例如：index=hashCode % arr.length（实际并非这样，后面讲解）,计算出index后，就会将该元素添加进去，理想状态下是将每个值都均匀的添加到数组中，但问题是不可能达到这样的理想状态，这时候就会产生哈希冲突，例如：小龙女通过计算添加到了数组3号位置，但是此时杨过这个元素通过计算产生了一个与小龙女相同的索引位置，这是就产生了哈希冲突

此时，就产生了第二种数据结构——链表，冲突的元素会在该索引处以链表的形式保存

但是当链表的长度过长时，其固有弊端就显现出来了，即查询效率较低，时间复杂度可能会达到O(n)级别，而数组的查询时间复杂度仅为O(1)

此时，就引出了第三种数据结构——红黑树，红黑树是一棵接近于平衡的二叉树，其查询时间复杂度为O(logn)，远远比链表的查询效率高。但如果链表长度不到一定的阈值，直接使用红黑树代替链表也是不行的，因为红黑树的自身维护的代价也是比较高的，每插入一个元素都可能打破红黑树的平衡性，这就需要每时每刻对红黑树再平衡（左旋、右旋、重新着色）

二、为什么数组的长度必须是2的指数次幂

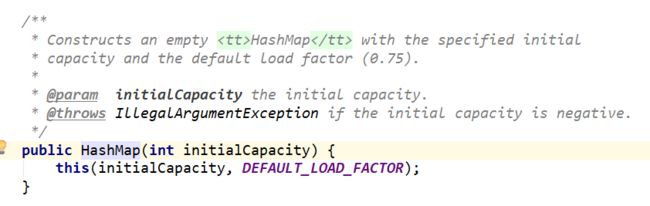
HashMap中数组的初始长度为16，我们创建一个空参的HashMap并点进源码如下图，从开发者提供的注释可以看到，空参的HashMap初始容量是16，，默认加载因子为0.75

此时我们再往HashMap随机传入一个参数，例如11

再点开其源码，发现其是空参方法的一个重载方法，即通过指定的初始值来创建一个HashMap，使用默认的加载因子仍是0.75，其通过this关键字调用了本类的另外一个重载方法

找到其调用的重载方法如下，我们可以看到，在方法中将初始容量和加载因子传入了进去并做了判断，即如果初始容量小于0，则抛出异常，如果出事容量大于了最大容量，则让其等于最大容量，同样对加载因子也做了判断，最后，设置了加载因子和其源码中定义的一个阈值，需要注意的是，这里的阈值使用了一个tableSizefor方法，它的作用是返回一个大于输入参数且最近的2的整数次幂的数

看一下tableSizefor方法如下，这里使用的是位运算，假设n的二进01xxx...xxx，接着对n右移1位001xx...xxx，再位或：011xx...xxx；对n右移2为00011...xxx，再位或：01111...xxx，此时前面已经有四个1了，再右移4位且位或可得8个1，同理，有8个1，右移8位肯定会让后八位也为1。综上可得，该算法让最高位的1后面的位全变为1。最后再让结果n+1，即得到了2的整数次幂的值了。cap-1再赋值给n的目的是让找到的目标值大于或等于原值

上面已经讲了HashMap是怎样将数组初始容量的长度转化为2的整数次幂的，那么为什么要把初始容量转成2的指数次幂呢？不转成2的指数次幂也是可以存储的啊，为什么要转？

• 首先看HashMap的put方法

其中的hash方法用于计算key的哈希值

我们一开始提到过，添加元素时索引的下标可以通过取模运算获得，但是我们知道计算机的运行效率：加法(减法)>乘法>除法>取模，取模的效率是最低的。所以我们要在HashMap中避免频繁的取模运算，又因为在我们HashMap中他要通过取模去定位我们的索引，并且HashMap是在不停的扩容，数组一旦达到容量的阈值的时候就需要对数组进行扩容。那么扩容就意味着要进行数组的移动，数组一旦移动，每移动一次就要重回记算索引，这个过程中牵扯大量元素的迁移，就会大大影响效率。那么如果说我们直接使用与运算，这个效率是远远高于取模运算的

• 再来看putVal方法，它是实现具体的put操作的方法,来看一下源码

    /**
     * Implements Map.put and related methods
     *
     * @param hash hash for key
     * @param key the key
     * @param value the value to put
     * @param onlyIfAbsent if true, don't change existing value
     * @param evict if false, the table is in creation mode.
     * @return previous value, or null if none
     */
	final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        Node[] tab; Node p; int n, i;
        //1. 如果当前table为空，新建默认大小的table
        if ((tab = table) == null || (n = tab.length) == 0)
            n = (tab = resize()).length;
        //2. 获取当前key对应的节点
        if ((p = tab[i = (n - 1) & hash]) == null)
            //3. 如果不存在，新建节点
            tab[i] = newNode(hash, key, value, null);
        else {
            //4. 存在节点
            Node e; K k;
            //5. key的hash相同，key的引用相同或者key equals，则覆盖
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
            //6. 如果当前节点是一个红黑树树节点，则添加树节点
            else if (p instanceof TreeNode)
                e = ((TreeNode)p).putTreeVal(this, tab, hash, key, value);
            //7. 不是红黑树节点，也不是相同节点，则表示为链表结构
            else {
                for (int binCount = 0; ; ++binCount) {
                    //8. 找到最后那个节点
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        //9. 如果链表长度超过8转成红黑树
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }
                    //10.如果链表中有相同的节点，则覆盖
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                //是否替换掉value值
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);
                return oldValue;
            }
        }
        //记录修改次数
        ++modCount;
        //是否超过容量，超过需要扩容
        if (++size > threshold)
            resize();
        afterNodeInsertion(evict);
        return null;
    }

由以上源码第2步，tab[i = (n - 1) & hash]中tab就是HashMap的实体数组，其下边通过i = (n - 1) & hash来获取（n表示数组长度，hash表示hashCode值），但是这必须保证数组长度为2的整数次幂，我们继续往下看

现在我们可以使用与运算(n-1) & hash取代取模运算hash%length，因为这两种方式记算出来的结果是一致的（n就是length），也就是(length-1)&hash = hash%length，例如：假设数组长度为4，哈希值为10

(n-1) & hash = (4-1) & 10 = 00000011 & 00001010 = 00000010 = 2
hash % length = 10 % 4 = 2

但是当数组的长=长度不为2的指数次幂时，两种方式计算的结果不一样，即length-1)&hash ≠ hash&length

例如：再假设数组长度为5，哈希值10

(n-1) & hash = (5-1) & 10 = 00000100 & 00001010 = 00000000 = 0
hash % length = 10 % 5 = 2

显然，当数组长度不为2的整数次幂时二者是不相等的

但最重要的一点，是要保证定位出来的值是在数组的长度之内的，不能超出数组长度，并且减少哈希碰撞，让每个位都可能被取到，我们来看下面例子

例如：(16-1) & hash
二进制的15：  0000 0000 0000 1111
hash(随机)   1101 0111 1011 0000
hash(随机)   1101 0111 1011 1111
结果         0000 0000 0000 0001 ~ 0000 0000 0000 1111
即得出的索引下标只能在0~15之间，保证了所有索引都在数组长度的范围内而不会越界，并且由于2的指数次幂-1都是...1111的形式的，即最后一位是1，这样，由于hash是随机的，进行与运算后每一位都是能取到的

反例：(7-1) & hash
二进制6： 0000 0000 0000 0110
hash     1011 1001 0101 0000
hash     1001 0001 0000 1111
结果      0000 0000 0000 0000 ~ 0000 0000 0000 0110
即得出的索引范围在0~6，虽然不会越界，但最后一位是0，即现在无论hash为何值，0001，0011，0101这几个值是不可能取到的，这就加剧了hash碰撞，并且浪费了大量数组空间，显然是我们不想看到的

总结：首先使用位运算来加快计算的效率，而要使用位运算，就需要数组-1然后与hash值保证其在数组范围内，只有当数组长度为2的指数次幂时，其计算得出的值才能和取模算法的值相等，并且保证能取到数组的每一位，减少哈希碰撞，不浪费大量的数组资源

三、为什么加载因子是0.75

加载因子如果定的太大，比如1，这就意味着数组的每个空位都需要填满，即达到理想状态，不产生链表，但实际是不可能达到这种理想状态，如果一直等数组填满才扩容，虽然达到了最大的数组空间利用率，但会产生大量的哈希碰撞，同时产生更多的链表，显然不符合我们的需求。

但如果设置的过小，比如0.5，这样一来保证了数组空间很充足，减少了哈希碰撞，这种情况下查询效率很高，但消耗了大量空间。

因此，我们就需要在时间和空间上做一个折中，选择最合适的负载因子以保证最优化，取到了0.75

四、为什么链表长度大于等于8时转成了红黑树

这里要提到一个概率论中的泊松分布，因为链表长度大于等于8时转成红黑树正是遵循泊松分布，先来看一下泊松分布

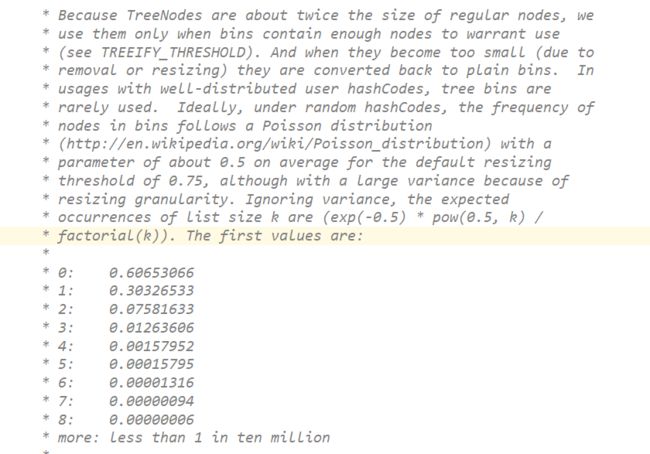
再看一下HashMap源码中注释对泊松分布的描述

意思就是HashMap节点分布遵循泊松分布，按照泊松分布的计算公式计算出了链表中元素个数和概率的对照表，可以看到链表中元素个数为8时的概率已经非常小。

另一方面红黑树平均查找长度是log(n)，长度为8的时候，平均查找长度为3，如果继续使用链表，平均查找长度为8/2=4，这才有转换为树的必要。链表长度如果是小于等于6，6/2=3，虽然速度也很快的，但是链表和红黑树之间的转换也很耗时。

当然，虽然在hashmap底层有这种红黑树的结构，但是我们要知道能产生这种结构的概率也不大，所以我们知道在 JDK1.7 到 JDK1.8 这其中HashMap的性能也只提高了7%~8% 左右