数据结构与算法——二叉树+带你实现表达式树（附源码）

作者介绍：22级树莓人（计算机专业），热爱编程＜目前在c＋＋阶段，因为最近参加新星计划算法赛道(白佬)，所以加快了脚步，果然急迫感会增加动力>——目标Windows，MySQL，Qt，数据结构与算法，Linux，多线程，会持续分享学习成果和小项目的
作者主页：king&南星
专栏链接：数据结构

欢迎各位→点赞 + 收藏 + 留言​
总结：希望你看完之后，能对你有所帮助，不足请指正！共同学习交流

---

‍二叉树

‍一、概念及定义

⛵1、概念

二叉树是一棵树，其中每个结点的儿子都不能多于两个

如下图是由一个跟和两个子树组成的二叉树，且子树可能为空

⛵2、性质

二叉树的一个性质是平均二叉树的深度要比N小得多。分析表明，这个平均深度为O(根号N),而对于特殊的二叉树，即二叉查找树，其深度的平均值为O(logN),不幸的是这个深度是可以大到N-1的，如下图所示

‍ 二、结点的定义、链表应用、空节点的说明

⛵1、结点声明

因为一颗二叉树最多有两个儿子，所以我们可以用指针直接指向他们。树节点的声明在结构体是类似于双链表的声明，在声明中，一个节点就是由关键字信息加上两个指向其他节点的指针(Lift和Right)组成的结构

//叶子节点数据
#define EMPTY 6666
//是否要显示EMPTY  为1 不显示EMPTY  为0 显示EMPTY
#define NOTSHOWEMPTY  1
typedef struct Node
{
	int data;
	struct Node* pLift;
	struct Node* pright;
}Node;

⛵2、链表的应用

在进行一次插入时需要调用malloc创建一个节点，节点可以在调用free删除后释放

Node* createNode(int newNodedata) 
{
	Node* newNode = malloc(sizeof(Node));
	if (NULL == newNode) return newNode;
	newNode->data = newNodedata;
	newNode->pLift = newNode->pright = NULL;
	return newNode;
}

⛵ 3、空结点的说明及画图

我们可以用链表的知识用矩形框画出二叉树，但是，树一般画成圆圈并用一些直线连接起来，因为二叉树实际上就是图，当涉及树时，我们也不显示地画出NULL指针，因为具有N个节点的每一颗二叉树都需要N+1个NULL指针，我们在这里描述的二叉树是无序二叉树，叶子节点用EMPTY节点表示

‍三、表达式树——遍历

⛵1、表达式树引入与介绍

下图是一个表达式树，表达式树的树叶是操作数，比如常量或变量，而其他的节点为操作符。由于这里所有的操作都是二元的，因此这颗特定的树正好是二叉树，虽然这是最简单的情况，但是节点含有的儿子还是有可能多于两个的。一个节点也有可能只有一个儿子，如具有一目操作符的情况。可以将通过递归计算左子树和右子树所得到的值应用在根处的算符操作中而算出表达式树T的值。在本例中，左子树的值为a+(b*c)，右子树的值为(((d*e)+f)*g),因此整颗表达式的值为a+(b*c)+(((d*e)+f)*g)

这里我们先看看我们这里用的数据

⛵2、中序遍历

我们可以通过递归产生一个带括号的左表达式，然后打印出在根处的运算符，然后再递归地产生一个带括号的右表达式而得到一个(对两个括号整体进行运算的)中缀表达式。这种一般的方法(左，根，右)被称为中序遍历

代码如下

void _midTravel(Node* root) 
{
	if (NULL == root) return;
	_midTravel(root->pLift);
#if NOTSHOWEMPTY
	if (root->data != EMPTY)
#endif
		printf("%d ", root->data);
	_midTravel(root->pright);
}

⛵3、后序遍历

就是递归打印出左子树，右子树，然后打印根节点，也就是后缀表达式，这种遍历一般称为后序遍历

代码如下

void _lstTravel(Node* root) 
{
	if (NULL == root) return;
	_lstTravel(root->pLift);
	_lstTravel(root->pright);
#if NOTSHOWEMPTY
	if (root->data != EMPTY)
#endif
		printf("%d ", root->data);
}

⛵4、先序遍历

先序遍历就是先打印出根节点，然后递归的打印出右子树和左子树，是一种前序记法

代码如下

void _preTravel(Node* root) 
{
	if (NULL == root) return;
#if NOTSHOWEMPTY
	if (root->data != EMPTY)
#endif
		printf("%d ", root->data);
	_preTravel(root->pLift);
	_preTravel(root->pright);
}

⛵5、总结

已知中序 和 先序 可以推导出树 知道后序
已知中序 和 后序 可以推导出树 知道先序
已知先序和后序，不能推导出树

这是因为只要知道先序和后序一个就可以知道根节点了，知道了中序就可以推导出左右子树了

⛵ 6、构建一颗表达式树

我们现在给出一种算法来把后缀表达式转换为表达式树。这种方法酷似后缀求值算法。一次一个符号地读入表达式，如果符号是操作数，那么我们就建立一个单节点树并将一个指向它的指针推入栈中。如果符号是操作符，那么我们就从栈中弹出指向两棵树T1和T2的两个指针(T1的先弹出）并形成一颗新的树，该树的根就是操作符，它的左右儿子分别指向T2和T1。然后将指向这棵树的指针压入栈中

来看一个例子，设输入为：ab+cde+**

⛵A、第一步

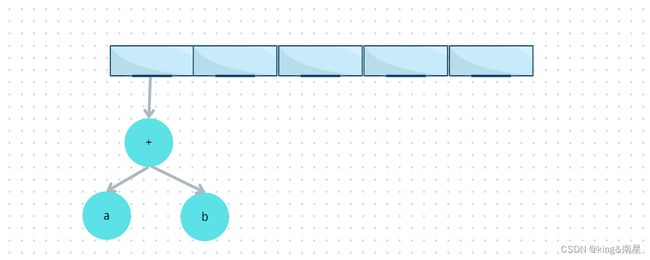
前两个符号是操作数，因此我们创建两颗单节点树并将指向它们的指针压入栈中

⛵B、第二步

接着，读入“+”,因此弹出指向这两颗树的指针，一棵新的树新成，而将指向该树的指针压入栈中

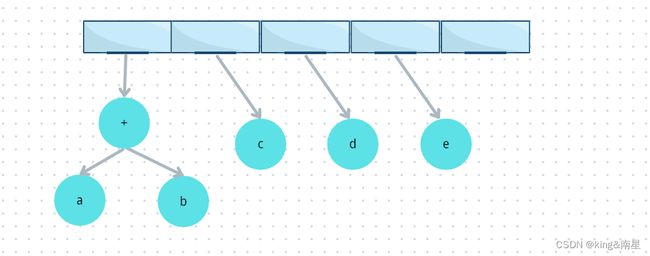
⛵C、第三步

然后，读入c、d、e，在每棵单节点树创建后，将指向对应的树的指针压入栈中

⛵D、第四步

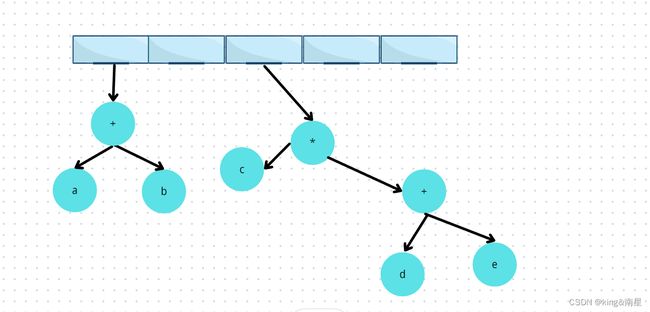
接下来读入“+”,因此两棵树合并

⛵E、第五步

继续进行，读入“”,因此，弹出两个树指针并形成一颗新的树，“”是它的根

⛵F、第六步

最后，读入最后一个符号，两棵树合并，而指向最后的树的指针留在栈中

‍⚖️四、查找节点

Node* findNode(Node* root, int findData) 
{
	if (NULL == root) return NULL;
	if (findData = EMPTY) return NULL;
	if (root->data == findData) return root;
	Node* pTemp = findNode(root->pLift, findData);
	if (pTemp) return pTemp;
	return findNode(root->pright, findData);
}

‍五、插入节点

这里就体现了递推的大用处了，还有就是要传二级指针，因为要修改根节点

//插入(先序遍历）
bool inserData(Node** root, int insertdata)
{
	if (NULL == root) return false;
	//插入根节点
	if( NULL == *root )
	{
		*root = createNode(insertdata);
		return true;
	}
	if ((*root)->data == EMPTY) return false;
	if (true == inserData(&((*root)->pLift), insertdata))
		return true;
	else
		return inserData(&((*root)->pright), insertdata);
}

‍六、综合代码

#include
#include
#include
#include
//叶子节点数据
#define EMPTY 6666
//是否要显示EMPTY  为1 不显示EMPTY  为0 显示EMPTY
#define NOTSHOWEMPTY  1
typedef struct Node
{
	int data;
	struct Node* pLift;
	struct Node* pright;
}Node;
//创建节点函数
Node* createNode(int newNodedata);
//PRE：先序遍历,MID：中序遍历,LST：后序遍历
enum travelType { PRE, MID, LST };
//遍历
void Travel(Node* root, enum travelType type);
//先序遍历
void _preTravel(Node* root);
//中序遍历
void _midTravel(Node* root);
//后序遍历
void _lstTravel(Node* root);
//插入(先序遍历）
bool inserData(Node** root, int insertdata);
//找到数据为findData的第一个节点 找到返回节点地址 否则返回NULL
Node* findNode(Node* root, int findData);
int main() 
{
	//一颗空树
	Node* pRoot = NULL;

	int arr[] = { 10, 99, 83, EMPTY, 22, EMPTY, EMPTY, EMPTY ,96,
		EMPTY, 56, 6, EMPTY, EMPTY, 11, 36, EMPTY, EMPTY, EMPTY,666 };


	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
		inserData(&pRoot, arr[i]);

	Travel(pRoot, PRE);
	Travel(pRoot, MID);
	Travel(pRoot, LST);

	return 0;
}
//创建节点函数
Node* createNode(int newNodedata) 
{
	Node* newNode = malloc(sizeof(Node));
	if (NULL == newNode) return newNode;
	newNode->data = newNodedata;
	newNode->pLift = newNode->pright = NULL;
	return newNode;
}
//遍历
void Travel(Node* root, enum travelType type) 
{
	switch (type)
	{
	case PRE:
		printf("先序遍历：");
		_preTravel(root);
		printf("\n");
		break;
	case MID:
		printf("中序遍历：");
		_midTravel(root);
		printf("\n");
		break;
	case LST:
		printf("后序遍历: ");
		_lstTravel(root);
		printf("\n");
		break;
	}
}
//先序遍历
void _preTravel(Node* root) 
{
	if (NULL == root) return;
#if NOTSHOWEMPTY
	if (root->data != EMPTY)
#endif
		printf("%d ", root->data);
	_preTravel(root->pLift);
	_preTravel(root->pright);
}
//中序遍历
void _midTravel(Node* root) 
{
	if (NULL == root) return;
	_midTravel(root->pLift);
#if NOTSHOWEMPTY
	if (root->data != EMPTY)
#endif
		printf("%d ", root->data);
	_midTravel(root->pright);
}
//后序遍历
void _lstTravel(Node* root) 
{
	if (NULL == root) return;
	_lstTravel(root->pLift);
	_lstTravel(root->pright);
#if NOTSHOWEMPTY
	if (root->data != EMPTY)
#endif
		printf("%d ", root->data);
}
//插入(先序遍历）
bool inserData(Node** root, int insertdata)
{
	if (NULL == root) return false;
	//插入根节点
	if( NULL == *root )
	{
		*root = createNode(insertdata);
		return true;
	}
	if ((*root)->data == EMPTY) return false;
	if (true == inserData(&((*root)->pLift), insertdata))
		return true;
	else
		return inserData(&((*root)->pright), insertdata);
}
//找到数据为findData的第一个节点 找到返回节点地址 否则返回NULL
Node* findNode(Node* root, int findData) 
{
	if (NULL == root) return NULL;
	if (findData = EMPTY) return NULL;
	if (root->data == findData) return root;
	Node* pTemp = findNode(root->pLift, findData);
	if (pTemp) return pTemp;
	return findNode(root->pright, findData);
}