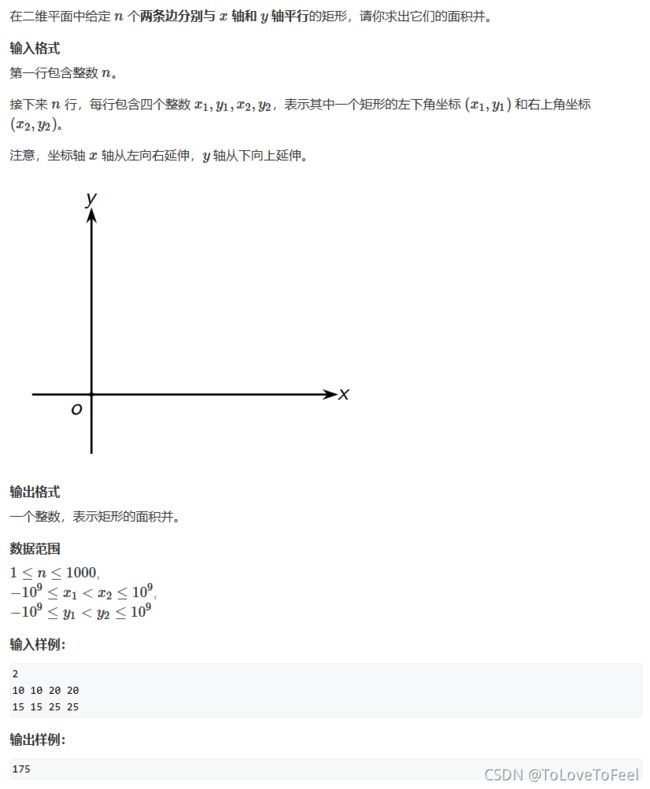
【算法专题】平面图形的面积并问题

平面图形的面积并问题

1. 概述

• 给定平面直角坐标系，坐标系中有若干图形，这些图形可以是三角形、多边形，圆形，甚至一些不规则的图形。这些图形可能会有重合的部分，我们在计算面积并的时候，重叠的部分只能计算一次。

• 一般来说求面积并存在如下方法：

  • （1）模拟（要求图形都是矩形，且矩形的四个顶点都在整点上），判断每个1x1的小矩形是否被至少一个图形覆盖一次，最后计算有多少小矩形被覆盖即可，对应例题：AcWing 3203. 画图；

  • （2）扫描线，一般使用线段树实现（要求都是矩形，且矩形的边要和坐标轴平行），对应例题：AcWing 3068. 扫描线、AcWing 1228. 油漆面积、AcWing 247. 亚特兰蒂斯、AcWing 2801. 三角形面积并；

  • （3）计算几何，对应例题：AcWing 2803. 凸多边形；

  • （4）自适应辛普森积分，对应例题：AcWing 3074. 自适应辛普森积分、AcWing 3069. 圆的面积并。

2. 例题

AcWing 3203. 画图

问题描述

• 问题链接：AcWing 3203. 画图

分析

• 本题使用模拟就可以解决。

• 使用每个格子的左下角表示格子，使用bool数组记录每个格子是否被染色，最后统计有多少格子被染色即可。

代码

• C++

#include 

using namespace std;

const int N = 110;
bool st[N][N];  // 标记该格子是否被图上颜色，每个格子用左下角的坐标定义为该格子的坐标

int n;

int main() {

    cin >> n;
    while (n--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        for (int i = x1; i < x2; i++)
            for (int j = y1; j < y2; j++)
                st[i][j] = true;
    }

    int res = 0;
    for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++)
            res += st[i][j];

    cout << res << endl;
    return 0;
}

AcWing 3068. 扫描线

问题描述

• 问题链接：AcWing 3068. 扫描线

分析

• 这里将出现的所有矩形以横坐标为分割线划分成一个个竖直的长条，计算每个长条的面积，相加就可以得到答案，如下图：

• 每个长条内部都是一堆等宽的小矩形，我们求出这些矩形在竖直方向上的长度，然后乘以宽度就是这个长条的面积。

• 如何求解每个长条竖直方向上的长度之和呢？首先遍历所有矩形，找到这个长条中所有的线段，然后使用区间合并即可。

• 关于区间合并可以参考：AcWing 803 区间合并。

• 本题的时间复杂度是：$O(n^2\times log(n))$。

代码

• C++

#include 
#include 
#include 
#include 

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int N = 1010;

int n;
PII l[N], r[N];  // 存储矩形左下角和右上角坐标
PII q[N];  // 存储每个竖直长条中线段

// 计算一个竖直长条的面积
LL range_area(int a, int b) {
    
    // 求需要合并的区间
    int cnt = 0;
    for (int i = 0; i < n; i++)
        if (l[i].x <= a && r[i].x >= b)
            q[cnt++] = {l[i].y, r[i].y};
    if (!cnt) return 0;
    
    // 合并区间、求区间长度并
    sort(q, q + cnt);
    LL res = 0;
    int st = q[0].x, ed = q[0].y;
    for (int i = 1; i < cnt; i++)
        if (q[i].x <= ed) ed = max(ed, q[i].y);
    	else {
            res += ed - st;
            st = q[i].x, ed = q[i].y;
        }
    res += ed - st;
    
    return res * (b - a);
}

int main() {
    
    scanf("%d", &n);
    vector<int> xs;
    for (int i = 0; i < n; i++) {
        scanf("%d%d%d%d", &l[i].x, &l[i].y, &r[i].x, &r[i].y);
        xs.push_back(l[i].x), xs.push_back(r[i].x);
    }
    
    sort(xs.begin(), xs.end());
    
    LL res = 0;
    for (int i = 0; i + 1 < xs.size(); i++)
        if (xs[i] != xs[i + 1])
            res += range_area(xs[i], xs[i + 1]);
    
    printf("%lld\n", res);
    
    return 0;
}

AcWing 1228. 油漆面积

问题描述

• 问题链接：AcWing 1228. 油漆面积

分析

• 本题是用扫描线问题。可以使用线段树求解。本题解法具有特殊性，只适用于这类题目。

• 我们可以在y轴方向上使用线段树求解，因为坐标都是整点，因此不需要使用离散化。线段树中的每个点代表的都是一段区间，叶节点代表长度为1的区间。

• 线段树节点存储的信息如下：

struct Node {
    int l, r;  // 区间左右端点，是整数
    int cnt;  // 当前区间[l, r]全部都被覆盖的次数
    double len;  // 不考虑祖先节点cnt的前提下，只考虑当前节点及子节点，cnt>0的区间总长度
}

• 假如线段树中某个节点l=0,r=0，则该节点代表y轴上的[0, 1]这一段区间的情况。

• 在操作之前我们需要将说有平行于y轴的边存储下来，可以使用一个结构体(x, y1, y2)，另外结构体中还存储一个k，如果这条边是矩形的左边，则k=1，如果是右边，则k=-1，表示对应y轴方向上应该加一还是减一。

• 因为本题对线段树的操作是：（1）对y轴上成对操作，且先加后减，意味着cnt>=0；（2）只需要根节点的len值。基于这两点，不需要使用pushdown操作。

• 线段树只能维护点，但是本题需要维护很多长度为1的区间，因此需要使用点代表区间，对应关系如下：[a, a+1]使用数字a表示。

• 有了上述表示之后，当我们要给纵坐标对应的区间 $[y_1,y_2]$ 加上一个值时，对应的是将线段树中的点 $y_1,y_1+1,...,y_2-1$ 都加上该值。

• 在本题上的基础上需要加上离散化才能解决的问题：AcWing 247. 亚特兰蒂斯。

• 本题的时间复杂度是：$O(n\times log(n))$的。

代码

• C++

#include 
#include 

using namespace std;

const int N = 10010;

int n;

struct Segment {
    int x, y1, y2;
    int k;
    
    bool operator< (const Segment &t) const {
        return x < t.x;
    }
} seg[N * 2];  // 存储竖边

struct Node {
    int l, r;
    int cnt;  // 该区间被覆盖次数
    int len;  // 该区间被覆盖长度
} tr[N * 4];

void pushup(int u) {
    
    if (tr[u].cnt > 0)  // 纵坐标对应区间[tr[u].l, tr[u].r+1]完全被覆盖
        tr[u].len = tr[u].r - tr[u].l + 1;
    else if (tr[u].l == tr[u].r)  // 叶节点没被覆盖，因此被覆盖长度为0
        tr[u].len = 0;
    else  // 不是叶节点且没有被完全覆盖
        tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}

void build(int u, int l, int r) {
    tr[u] = {l, r};
    if (l != r) {
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    }
}

void modify(int u, int l, int r, int k) {
    if (tr[u].l >= l && tr[u].r <= r) {
        tr[u].cnt += k;
        pushup(u);
    } else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, k);
        if (r > mid) modify(u << 1 | 1, l, r, k);
        pushup(u);
    }
}

int main() {
    
    cin >> n;
    for (int i = 0, j = 0; i < n; i++) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        seg[j++] = {x1, y1, y2, 1};
        seg[j++] = {x2, y1, y2, -1};
    }
    
    sort(seg, seg + n * 2);
    
    build(1, 0, 10000);
    
    int res = 0;
    for (int i = 0; i < n * 2; i++) {
        if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);
        modify(1, seg[i].y1, seg[i].y2 - 1, seg[i].k);
    }
    
    cout << res << endl;
    
    return 0;
}

AcWing 247. 亚特兰蒂斯

问题描述

• 问题链接：AcWing 247. 亚特兰蒂斯

分析

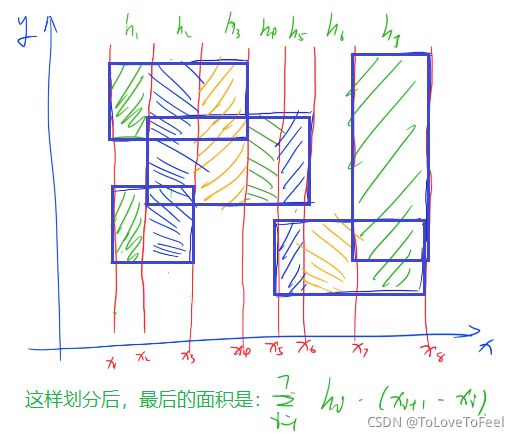
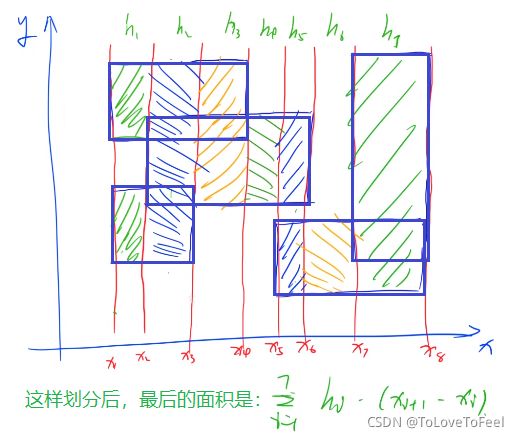
• 本题需要用到扫描线技巧。我们可以统计出所有矩形对应四个顶点的横坐标，过这些横坐标做x的垂线（即扫描线），如下图：

• 在沿着扫描线从左向右扫描的过程中，我们可以求解每个h的大小，我们可以这样操作：对于每个矩形与y轴平行的两个边，左边的权值记为+1，右边的权值记为-1（如下图）：

• 如果当前扫描线上是+1的话，将沿y轴方向的对应区间全部加上1，如果是-1的话，全部加上-1（区间上对应的数表示当前区间被多少个矩形覆盖）；为了求出对应的h，我们需要统计出沿y轴的整个区间内大于0的区间长度总和；因此，总结一下，我们存在两个操作：

  （1）对于某个区间加上一个数；

  （2）统计出整个区间中大于0的区间的长度和；

• 上面的操作对应区间修改、区间查询，因此可以使用线段树来求解，线段树中每个节点存储的信息如下：

struct Node {
    int l, r;  // 区间左右端点，这里是纵坐标离散化后对应的值，是整数
    int cnt;  // 当前区间[l, r]全部都被覆盖的次数
    double len;  // 不考虑祖先节点cnt的前提下，只考虑当前节点及子节点，cnt>0的区间总长度，类似于刚才(Acwing 243)的sum
}

• 此时，本题的基本做法已经讲解完毕，但是我们维护cnt和len比较麻烦，所以我们考虑是否能根据此问题的性质进行优化，最终优化的结果是我们不需要进行pushdown操作，分析如下：

• 我们注意到本题中的线段树具有如下性质：

  （1）因为我们求扫描线上总高度h，所以我们在查询的时候只会使用到根节点的信息；可以看到query的基本结构如下：

  int query(int u, int l, int r) {
      if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;  // 对于本题，这句话一定会被执行，因此pushdwon执行不到
      
      pushdown(u);
  	// ......
  }
  

  从上面的代码中我们发现，query中的pushdown永远不会被执行到。

  （2）因为矩形存在两条边和y轴平行，因此线段树中所有的操作一定都是成对出现的（所谓成对出现，指的是我们对于某个区间加上一个1，则一定会在之后的操作中再将同样的一个区间减去一个1），且先加后减。可以看到modify的基本结构如下：

  void modify(int u, int l, int r, LL d) {
      if (tr[u].l >= l && tr[u].r <= r) {
          tr[u].sum += (LL)(tr[u].r - tr[u].l + 1) * d;
          tr[u].add += d;
      } else {
          pushdown(u);  // 这句话是多余的
          // ......
          pushup(u);
      }
  }
  

  核心：操作的区间是相同的，且先加1后减1。假设modify是给某个区间减1，则这之前这个区间一定都被加过1，对应线段树中的节点（是个集合，记为A）一定有该懒标记，减1的时候一定再会将A中所有的懒标记恢复到加1前的状态，因此，没必要把当前父节点的修改信息下传到子节点，也就是没必要使用pushdown操作。

• 这一题不用pushdown是因为这个题目十分特殊，可以说这种做法就是针对这个题目的，因此可以单独记下来。

• 另外这一题中坐标都是小数，我们存储纵坐标的时候需要进行离散化，这里使用vector对纵坐标进行离散化。因为图中有n个矩形，所以平行于y轴的边有$2n$条，因此我们需要存储$2n$个区间，每个区间（平行于y轴的线段）存储一个横坐标，两个纵坐标，并且需要按照横坐标从小到大的顺序排序，存储线段可以使用结构体，如下：

struct Segment
{
    double x, y1, y2;  // 区间的两个端点为(x, y1), (x, y2)
    int k;  // k只能取+1或者-1，表示当前区间的操作是+1还是-1
    bool operator< (const Segment &t) const {  // 让结构体可以从小到大排序
        return x < t.x;
    }
}

• 我们线段树中维护的内容是一个个的区间，一共$2n$个，因此线段树大小要开到$8n$的大小。

• 这些区间的纵坐标需要放到ys（是一个vector）中，进行离散化（保序离散化，因为我们要判断区间的包含关系），离散化过程：排序，去重；然后通过lower_bound可以找到每个y在vector中的下标；ys[0]表示最小的一个纵坐标值。

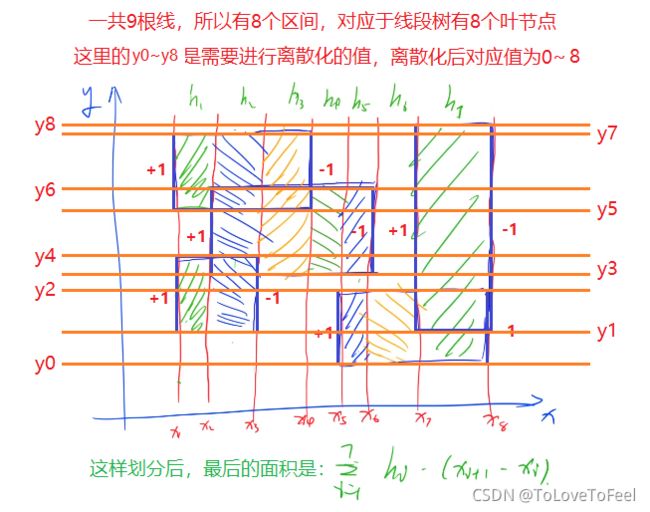
• 线段树中需要维护$2n$个区间，因此线段树中的每个节点代表一个区间，假设某个区间是是$(y_i,y_{i+1})$，且$y_i$和$y_{i+1}$之间没有其他的y了，则该区间对应于线段树中的叶节点，则如果$ys[l1]=y_i,ys[r1]=y_{i+1}$，对应的线段树的区间是$[l1,r1]$，另外注意这里的$(y_i,y_{i+1})$可能不是矩形的某条边，如上图中扫描线$x_8$对应的情况。这里的$x_8$对应线段树中的三个区间（只单纯的考虑后面两个矩形的情况下是3个，否则不是）

• 具体来说，上图中存在的最小区间个数为8个，因此线段树中的叶节点也是8个：

• 因此线段树中的某个"点"对应于图中是某段区间，比如根节点对应于上图中的区间$[y_0,y_7]$。

• 如上图，这些小区间分别是 $[y_0,y_1]、[y_1,y_2]、...、[y_7,y_8]$，他们的长度组成一个数组a，其中a[0]表示第一个区间的长度，对应离散化区间为[0,1]。

• a[0~2]表示第一个区间的长度，对应离散化区间为[0,1]、[1, 2]、[2, 3]，原区间为[ys[0], ys[2+1]] = $[y_0,y_3]$。

• 当我们要更新$[y_3,y_6]$这一段区间，相当于更新a[3~5]，对应于$a[find(y_3)...(find(y_6))-1]$（find函数返回离散化后的值）。

代码

• C++

#include 
#include 
#include 

using namespace std;

const int N = 100010;

int n;  // 矩形个数
struct Segment {
    double x, y1, y2;  // 区间的两个端点为(x, y1), (x, y2)
    int k;  // k只能取+1或者-1，表示当前区间的操作是+1还是-1
    bool operator< (const Segment &t) const {
        return x < t.x;
    }
} seg[N * 2];  // 存储区间

struct Node {
    int l, r;  // 纵坐标对应的离散化的值
    int cnt;  // 当前区间[l, r]全部都被覆盖的次数
    // 不考虑祖先节点cnt的前提下，只考虑当前节点及子节点，cnt>0的区间总长度，类似于刚才(Acwing 243)的sum
    double len;
} tr[N * 8];

vector<double> ys;  // 用于离散化纵坐标

int find(double y) {
    return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}

void pushup(int u) {
    
    if (tr[u].cnt) {  // 说明节点u对应的区间完全被覆盖
        // 例如tr[u].l = 3, tr[u].r = 5, 对应上面分析的于a[3],a[4],a[5]三个区间
        // 对应上面的[ys[3], ys[4]], [ys[4], ys[5]], [ys[5], ys[6]]
        // 即[y3, y4], [y4, y5], [y5, y6]
        tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];
    } else if (tr[u].l != tr[u].r) {  // 没有完全被覆盖，且有子区间
        tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
    } else {  // 没有完全覆盖，且是叶节点
        tr[u].len = 0;
    }
}

void build(int u, int l, int r) {
    
    tr[u] = {l, r, 0, 0};
    if (l != r) {
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    }
}

// 从节点u开始将区间[l, r]加上k
void modify(int u, int l, int r, int k) {
    
    if (tr[u].l >= l && tr[u].r <= r) {
        tr[u].cnt += k;
        pushup(u);
    } else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r , k);
        if (r > mid) modify(u << 1 | 1, l, r, k);
        pushup(u);
    }
}

int main() {
    
    int T = 1;
    while (scanf("%d", &n), n) {
        
        ys.clear();
        for (int i = 0, j = 0; i < n; i++) {
            double x1, y1, x2, y2;
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            seg[j++] = {x1, y1, y2, 1};
            seg[j++] = {x2, y1, y2, -1};
            ys.push_back(y1), ys.push_back(y2);
        }
        
        // 对纵坐标进行离散化
        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());
        
        // ys.size()个纵坐标，ys.size()-1个区间，下标是0~ys.size() - 2
        build(1, 0, ys.size() - 2);
        // 按照横坐标排序(横坐标当成扫描线)
        sort(seg, seg + n * 2);
        
        double res = 0;
        for (int i = 0; i < 2 * n; i++) {
            if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);
            modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);
        }
        
        printf("Test case #%d\n", T ++ );
        printf("Total explored area: %.2lf\n\n", res);
    }
    
    return 0;
}

AcWing 2801. 三角形面积并

问题描述

• 问题链接：AcWing 2801. 三角形面积并

分析

• 本题中坐标系中的图形是三角形，不同于矩形，矩形之间相交则交点的坐标必定等于某两个矩形的横坐标和纵坐标，因此扫描线的数量和矩形的数量成比例。

• 但是三角形之间的交点不具有上述特点，对于n个三角形而言，最坏可能形成 $n^2$ 级别个交点，因此本题三角形的数量不能太大。

• 基本思路还是扫描线，根据三角形所有横坐标以所有交点的横坐标为分界线，然后求解每个竖直长条之间的面积即可。如下图：

• 对于每个竖直长条面积的求解，可以将每个竖直长条的部分看成若干个梯形（三角形，四边形都可以看成特殊梯形，使用梯形面积公式计算都是正确的），求解这些梯形的面积并即可。

• 因为梯形面积为：（上底+下底）x高/2，因此我们将所有上底的长度并求出来，以及下底长度并求出来，然后乘以高除以2即可。

• 时间复杂度：$O(n^3\times log(n))$。

代码

• C++

#include 
#include 
#include 
#include 
#include 

#define x first
#define y second

using namespace std;

typedef pair<double, double> PDD;
const int N = 110;
const double eps = 1e-8, INF = 1e6;

int n;
PDD tr[N][3];  // 存储三角形的顶点
PDD q[N];  // 存储待合并的区间

int sign(double x) {
    if (fabs(x) < eps) return 0;
    if (x < 0) return -1;
    return 1;
}

int dcmp(double x, double y) {
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 1;
}

PDD operator+ (PDD a, PDD b) {
    return {a.x + b.x, a.y + b.y};
}

PDD operator- (PDD a, PDD b) {
    return {a.x - b.x, a.y - b.y};
}

PDD operator* (PDD a, double t) {
    return {a.x * t, a.y * t};
}

double operator* (PDD a, PDD b) {  // 叉积
    return a.x * b.y - a.y * b.x;
}

double operator& (PDD a, PDD b) {  // 点积
    return a.x * b.x + a.y * b.y;
}

// 判断点p是否在线段(a, b)上
bool on_segment(PDD p, PDD a, PDD b) {
    return sign((p - a) & (p - b)) <= 0;
}

// 求解两个先点的交点，不存在交点的话返回{INF, INF}
PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w) {
    
    if (!sign(v * w)) return {INF, INF};
    auto u = p - q;
    auto t = w * u / (v * w);
    auto o = p + v * t;
    if (!on_segment(o, p, p + v) || !on_segment(o, q, q + w))
        return {INF, INF};
    return o;
}

double line_area(double a, int side) {
    
    int cnt = 0;  // x=a上线段的个数
    for (int i = 0; i < n; i ++ ) {
        
        auto t = tr[i];
        if (dcmp(t[0].x, a) > 0 || dcmp(t[2].x, a) < 0) continue;
        
        if (!dcmp(t[0].x, a) && !dcmp(t[1].x, a)) {  
            // 三角形一条边在x=a上, 另一个点在x=a右侧
            if (side)
                q[cnt ++ ] = {t[0].y, t[1].y};  // 线段端点大小不确定
        } else if (!dcmp(t[2].x, a) && !dcmp(t[1].x, a)) {
            // 三角形一条边在x=a上, 另一个点在x=a左侧
            if (!side) 
                q[cnt ++ ] = {t[2].y, t[1].y};  // 线段端点大小不确定
        } else {
            // 求三条边和x=a的交点，可能三个交点，也可能两个交点
            // 三个交点是因为：三角形有个顶点在x=a上
            double d[3];
            int u = 0;
            for (int j = 0; j < 3; j ++ ) {
                // x=a这条直线的两个端点(a, -INF), (a, +INF)
                // 因此点向式为：(a, -INF), (0, INF * 2)
                auto o = get_line_intersection(t[j], t[(j + 1) % 3] - t[j], {a, -INF}, {0, INF * 2});
                if (dcmp(o.x, INF))
                    d[u ++ ] = o.y;
            }
            if (u) {
                sort(d, d + u);
                q[cnt ++ ] = {d[0], d[u - 1]};
            }
        }
    }
    
    if (!cnt) return 0;
    
    // 需要保证每个区间左端点小于右端点
    for (int i = 0; i < cnt; i ++ )
        if (q[i].x > q[i].y)
            swap(q[i].x, q[i].y);

    // 区间合并求区间长度
    sort(q, q + cnt);
    double res = 0, st = q[0].x, ed = q[0].y;
    for (int i = 1; i < cnt; i ++ )
        if (q[i].x <= ed) ed = max(ed, q[i].y);
        else {
            res += ed - st;
            st = q[i].x, ed = q[i].y;
        }
    res += ed - st;
    return res;
}

double range_area(double a, double b) {
    
    // 1: 表示右边, 0: 表示左边
    return (line_area(a, 1) + line_area(b, 0)) * (b - a) / 2;
}

int main() {
    
    scanf("%d", &n);
    vector<double> xs;  // 存储顶点和交点的横坐标
    for (int i = 0; i < n; i ++ ) {
        for (int j = 0; j < 3; j ++ ) {
            scanf("%lf%lf", &tr[i][j].x, &tr[i][j].y);
            xs.push_back(tr[i][j].x);
        }
        // 为了方便在line_area中判断三角形和扫描线划分的区间是否有交集
        sort(tr[i], tr[i] + 3);
    }
    
    // 求解三角形边之间的交点
    for (int i = 0; i < n; i ++ )
        for (int j = i + 1; j < n; j ++ )
            for (int x = 0; x < 3; x ++ )
                for (int y = 0; y < 3; y ++ ) {
                    auto o = get_line_intersection(tr[i][x], tr[i][(x + 1) % 3] - tr[i][x],
                                                    tr[j][y], tr[j][(y + 1) % 3] - tr[j][y]);
                    if (dcmp(o.x, INF))
                        xs.push_back(o.x);
                }
    
    sort(xs.begin(), xs.end());
    
    double res = 0;
    for (int i = 0; i + 1 < xs.size(); i ++ )
        if (dcmp(xs[i], xs[i + 1]))
            res += range_area(xs[i], xs[i + 1]);
    
    printf("%.2lf\n", res);
    
    return 0;
}

AcWing 2803. 凸多边形

问题描述

• 问题链接：AcWing 2803. 凸多边形

分析

• 半平面交：给定一条直线，则只保留直线左侧的一半；这样给定多条直线后，平面上很多区域都被删除，剩余的部分被称为半平面交。

• 本题求解多个凸多边形的面积交，我们可以把每个图形的每条边看成一条直线，表示直线的向量是逆时针的，这样所有凸多边形的面积并就变为了求所有直线得到的半平面交对应的面积。下面是求解半平面交的讲解：

• （1）首先将所有直线按照角度从小到大排序；

• （2）使用双端队列q维护当前半平面交中存在的直线，依次遍历所有直线，用当前遍历的直线更新q的队头和队尾。如果队头或者队尾的两个直线的交点在当前直线的右侧，则删除队列中的一个元素。

• （3）使用队尾元素更新队首元素，使用队首元素更新队尾元素。

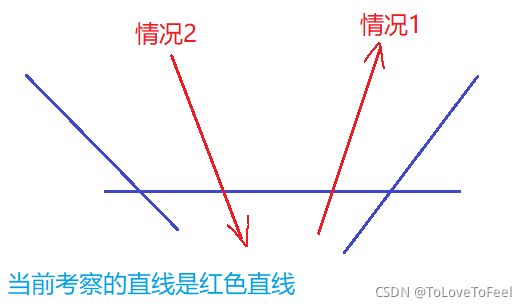
• 这里需要用当前遍历的直线更新队首和队尾元素是因为存在如下两种情况：

代码

• C++

#include 
#include 
#include 
#include 

#define x first
#define y second

using namespace std;

typedef pair<double, double> PDD;

const int N = 510;
const double eps = 1e-8;

int cnt;  // 存储直线的数量
struct Line {
    PDD st, ed;
} line[N];  // 存储直线上的两个点
PDD pg[N];  // 存储某个多边形上所有点
PDD ans[N];  // 存储交集对应多边形上的点
int q[N];  // 双端队列

int sign(double x) {
    if (fabs(x) < eps) return 0;
    if (x < 0) return -1;
    return 1;
}

int dcmp(double x, double y) {
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 1;
}

double get_angle(const Line &a) {  // 获取直线a和x轴的角度
    return atan2(a.ed.y - a.st.y, a.ed.x - a.st.x);
}

PDD operator-(PDD a, PDD b) {
    return {a.x - b.x, a.y - b.y};
}

double cross(PDD a, PDD b) {
    return a.x * b.y - a.y * b.x;
}

double area(PDD a, PDD b, PDD c) {
    return cross(b - a, c - a);
}

// 直线按照和x轴角度排序函数
bool cmp(const Line &a, const Line &b) {
    double A = get_angle(a), B = get_angle(b);
    if (!dcmp(A, B)) return area(a.st, a.ed, b.ed) < 0;  // 角度相同靠左的直线排在前面
    return A < B;
}

// 获取直线 p+vt 和 q+wt 的交点
PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w) {
    auto u = p - q;
    double t = cross(w, u) / cross(v, w);
    return {p.x + v.x * t, p.y + v.y * t};
}

PDD get_line_intersection(Line a, Line b) {
    return get_line_intersection(a.st, a.ed - a.st, b.st, b.ed - b.st);
}

// 判断bc的交点是否在a的左侧
bool on_right(Line &a, Line &b, Line &c) {
    auto o = get_line_intersection(b, c);
    return sign(area(a.st, a.ed, o)) <= 0;
}

// 求解半平面交
double half_plane_intersection() {
    
    sort(line, line + cnt, cmp);
    int hh = 0, tt = -1;
    for (int i = 0; i < cnt; i++) {
        // 当前直线和一条直线平行，跳过即可(因为更靠右)
        if (i && !dcmp(get_angle(line[i]), get_angle(line[i - 1]))) continue;
        // 更新队尾元素
        while (hh + 1 <= tt && on_right(line[i], line[q[tt - 1]], line[q[tt]])) tt--;
        // 更新队头元素
        while (hh + 1 <= tt && on_right(line[i], line[q[hh]], line[q[hh + 1]])) hh++;
        q[++tt] = i;
    }
    
    // 使用队头元素更新队尾元素
    while (hh + 1 <= tt && on_right(line[q[hh]], line[q[tt - 1]], line[q[tt]])) tt--;
    // // 使用队尾元素更新队头元素
    // while (hh + 1 <= tt && on_right(line[q[tt]], line[q[hh]], line[q[hh + 1]])) hh++;
    
    q[++tt] = q[hh];
    int k = 0;
    for (int i = hh; i < tt; i++)
        ans[k++] = get_line_intersection(line[q[i]], line[q[i + 1]]);
    
    // 求解多边形的面积: 从第一个顶点出发把凸多边形分成n − 2个三角形，然后把面积加起来
    double res = 0;
    for (int i = 1; i + 1 < k; i++)
        res += area(ans[0], ans[i], ans[i + 1]);
    return res / 2;
}

int main() {
    
    int n, m;
    scanf("%d", &n);
    while (n--) {
        scanf("%d", &m);
        for (int i = 0; i < m; i++) scanf("%lf%lf", &pg[i].x, &pg[i].y);
        for (int i = 0; i < m; i++)
            line[cnt++] = {pg[i], pg[(i + 1) % m]};
    }
    
    double res = half_plane_intersection();
    
    printf("%.3lf\n", res);
    
    return 0;
}

AcWing 3074. 自适应辛普森积分

问题描述

• 问题链接：AcWing 3074. 自适应辛普森积分

分析

• 辛普森积分是插值函数的一个应用，给定一个函数f(x)，我们可以用如下公式求解函数在区间[a, b]之间的有向面积：

$$S=\frac{b-a}{6}(f(a)+4\times f(\frac{a+b}{2})+f(b))$$

• 所谓自适应辛普森积分：假设我们当前用辛普森积分求得的面积为s，接着我们将每个区间分为两部分，返回两部分的面积和left、right，如果left+right-s的绝对值小于给定阈值，则停止分割，返回当前结果。

代码

• C++

#include 
#include 
#include 
#include 

using namespace std;

const double eps = 1e-12;

double f(double x) {
    return sin(x) / x;
}

double simpson(double l, double r) {
    auto mid = (l + r) / 2;
    return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;
}

double asr(double l, double r, double s) {
    auto mid = (l + r) / 2;
    auto left = simpson(l, mid), right = simpson(mid, r);
    if (fabs(left + right - s) < eps) return left + right;
    return asr(l, mid, left) + asr(mid, r, right);
}

int main() {
    
    double l, r;
    scanf("%lf%lf", &l, &r);
    
    printf("%lf\n", asr(l, r, simpson(l, r)));
    
    return 0;
}

AcWing 3069. 圆的面积并

问题描述

• 问题链接：AcWing 3069. 圆的面积并

分析

• 本题使用辛普森积分解决。关键在于定义f(x)，这里f(a)定义为x=a这条直线和圆交集的线段的长度并。

• 求直线和圆相交的线段长度可以使用勾股定理。

代码

• C++

#include 
#include 
#include 
#include 

#define x first
#define y second

using namespace std;

typedef pair<double, double> PDD;
const int N = 1010;
const double eps = 1e-8;

int n;
struct Circle {
    PDD r;
    double R;
} c[N];
PDD q[N];

int dcmp(double x, double y) {
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 1;
}

double f(double x) {
    
    int cnt = 0;
    for (int i = 0; i < n; i ++ ) {
        auto X = fabs(x - c[i].r.x), R = c[i].R;
        if (dcmp(X, R) < 0) {
            auto Y = sqrt(R * R - X * X);
            q[cnt ++ ] = {c[i].r.y - Y, c[i].r.y + Y};
        }
    }
    
    if (!cnt) return 0;
    
    sort(q, q + cnt);
    double res = 0, st = q[0].x, ed = q[0].y;
    for (int i = 1; i < cnt; i ++ )
        if (q[i].x <= ed) ed = max(ed, q[i].y);
        else {
            res += ed - st;
            st = q[i].x, ed = q[i].y;
        }
    return res + ed - st;
}

double simpson(double l, double r) {
    
    auto mid = (l + r) / 2;
    return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;
}

double asr(double l, double r, double s) {
    auto mid = (l + r) / 2;
    auto left = simpson(l, mid), right = simpson(mid, r);
    if (fabs(s - left - right) < eps) return left + right;
    return asr(l, mid, left) + asr(mid, r, right);
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
        scanf("%lf%lf%lf", &c[i].r.x, &c[i].r.y, &c[i].R);
        
    double l = -2000, r = 2000;
    printf("%.3lf\n", asr(l, r, simpson(l, r)));
    
    return 0;
}