6.Python之动态规划

6.1 概念

动态规划（DP）的思想 = 最优子结构（递推式）+ 重复子问题（把子问题的计算结果存起来。后面子问题直接拿前面的来用。

递归算法由于重复求解相同子问题，效率极低。

动态规划的思想：

• 每个子问题只求解一次，保存求解结果
• 之后需要此问题时，只需要查找保存的结果

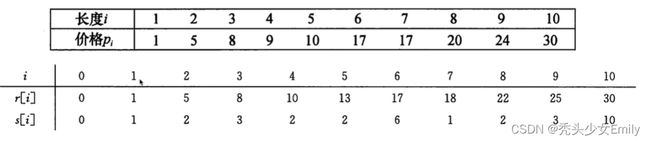
6.2 钢条切割问题

本质就是，前面每个长度的价格都是累计的最优结果。所以计算后面的价格只需要考虑不分割或跟哪个长度组合最优就好了。

 最优子结构：

• 可以将求解规模为n的原问题，划分为规模更小的子问题：完成一次切割后，可以将产生的两端钢条看成两个独立的钢条切割问题；
• 组合两个字问题的最优解，并在所有可能的两段切割方案中选取组合收益最大的，构成原问题的最优解；
• 钢条切割满足最优子结构：问题的最优解由相关子问题的最优解组合而成，这些子问题可以独立求解。

p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]

# 计算太慢，重复计算两次
def cut_rod_recurision_1(p, n):
    if n == 0:
        return 0
    else:
        res = p[n]
        for i in range(1, n):
            res = max(res, cut_rod_recurision_1(p, i) + cut_rod_recurision_1(p, n-i))
        return res


def cut_rod_recurision_2(p, n):
    if n == 0:
        return 0
    else:
        res = 0
        for i in range(1,n+1):
            res = max(res, p[i] + cut_rod_recurision_2(p, n-i))
        return res

print(cut_rod_recurision_1(p, 9))
print(cut_rod_recurision_2(p, 9))
# 动态规划写法
def cut_rod_dp(p, n):
    r = [0]
    for i in range(1, n+1):
        res = 0
        for j in range(1, i+1):
            res = max(res, p[j] + r[i-j])
        r.append(res)
    return r[n]

重构解：如何修改动态规划算法，使其不仅输出最优解，还输出最优切割方案？

对每个子问题，保存切割一次时左边切下的长度

 s[i]表示：对于当前i钢条，最优方案对应的左边这一块的长度是多少，也就是说切一刀下去不切的部分是多少。

def cut_rod_extend(p, n):
    r = [0]
    s = [0]
    for i in range(1, n+1):
        res_r = 0  # 价格最大值
        res_s = 0  # 价格最大值对应方案的左边不切割部分的长度
        for j in range(1, i + 1):
           if p[j] + r[i - j] > res_r:
              res_r = p[j] + r[i - j]
              res_s = j
        r.append(res_r)
        s.append(res_s)
    return r[n], s


# 输出方案
def cut_rod_solution(p, n):
    r, s = cut_rod_extend(p, n)
    ans = []
    while n > 0:
        ans.append(s[n])
        n -= s[n]
    return ans


print(cut_rod_dp(p, 20))
print(cut_rod_solution(p, 20))

动态规划问题关键特征：

什么问题可以使用动态规划方法？

1.最优子结构：

• 原问题的最优解中涉及多少个子问题
• 在确定最优解使用哪些子问题时，需要考虑多少种选择

2.重叠子问题

6.3 最长公共子序列

一个序列的子序列是在该序列中山区若干元素后得到的序列。例：“ABCD”和“DBF”都是“ABCDEFG”的子序列。

最长公共子序列（LCS）问题：给定两个序列X和Y，求X和Y长度最大的公共子序列。例：X=“ABBCBDE”　Y＝“DBBCDB”　LCS(X, Y)=“BBCD”

应用场景：字符串相似度比对

思考：

• 暴力穷举法的时间复杂度是多少？
• 最长公共子序列是否具有最优子结构性质？

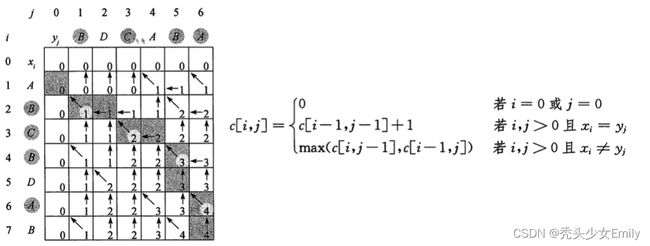
 例：要求a = "ABCDAB"与b = "BDCABA"的LCS：

        由于最后一位"B"≠"A"：

                因此LCS(a, b)应该来源于LCS(a[:-1], b)与LCS(a, b[:-1])中更大的那一个

def lcs_length(x, y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n+1)] for _ in range(m+1)]  # 得空出一行一列，所以要构造m+1行，n+1列
    for i in range(1, m+1):  # 1到m
        for j in range(1, n+1):  # 1到n
            if x[i-1] == y[j-1]:  # i j位置上的字符匹配的时候，如果匹配是来自于左上方+1
                c[i][j] = c[i-1][j-1] + 1
            else:
                c[i][j] = max(c[i-1][j],c[i][j-1])
    for _ in c:
        print(_)
    return c[m][n]


def lcs(x, y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    b = [[0 for _ in range(n + 1)] for _ in range(m + 1)]  # 1：左上方；2：上方；3：左方
    for i in range(1, m + 1):  # 1到m
        for j in range(1, n + 1):  # 1到n
            if x[i - 1] == y[j - 1]:  # i j位置上的字符匹配的时候，如果匹配是来自于左上方+1
                c[i][j] = c[i - 1][j - 1] + 1
                b[i][j] = 1  # 左上方来的
            elif c[i-1][j] > c[i][j-1]:  # 来自上方
                c[i][j] = c[i-1][j]
                b[i][j] = 2
            else:  # 来自左方
                c[i][j] = c[i][j-1]
                b[i][j] = 3
    return c[m][n], b


def lcs_trackback(x, y):
    c, b = lcs(x, y)
    i = len(x)
    j = len(y)
    res = []
    while i > 0 and j > 0:
        if b[i][j] == 1:  # 来自左上=>匹配
           res.append(x[i-1])
           i -= 1
           j -= 1
        elif b[i][j] == 2:  # 来自上方=>不匹配
            i -= 1
        else:  # 来自左方=>不匹配
            j -= 1
    return ''.join(reversed(res))


print(lcs_trackback('ABCBADB', 'BDCABA'))
# print(lcs_length('ABCBDAB', 'BDCABA'))
# c, b = lcs('ABCBDAB', 'BDCABA')
# for _ in b:
#     print(_)