BBR到底好在哪里?
BBR到底好在哪里?
都说BBR好,特别是在长传场景,一试就知道,也有很多分析BBR细节的文章,但很少有在理论上详细对比BBR和传统Loss based CCA的,BBR到底好在哪里,周末例行写作,今天的主题就是它了。
先从抗丢包说起。BBR的抗丢包能力很强,这从BBR paper里的一张图中可以看出来:

该图的注释如下:
Figure 8 shows BBR vs. CUBIC goodput for 60-second flows on a 100-Mbps/100-ms link with 0.001 to 50 percent random loss. CUBIC’s throughput decreases by 10 times at 0.1 percent loss and totally stalls above 1 percent. The maximum possible throughput is the link rate times fraction delivered (= 1 - lossRate). BBR meets this limit up to a 5 percent loss and is close up to 15 percent.
只要丢包率在20%以内,BBR的吞吐似乎不受丢包的影响,但这是为什么?下面简单推导一下BBR的理论最好表现。
设丢包率为 p p p,BltBW为 b b b,很显然有效传输率为 1 − p 1-p 1−p,BBR在ProbeBW状态的1.25倍速的up probe探测,若要抵消丢包,维持带宽 b b b,则必须保证:
1.25 b ( 1 − p ) = b 1.25b(1-p)=b 1.25b(1−p)=b
解得 p p p的值为 0.2 0.2 0.2,也就是 20 % 20\% 20%,正中上图。如果我们把固定的增益系数 1.25 1.25 1.25抽象成一个可以调节的参数,那么会得到一个在该增益系数下的丢包率崖点:
p = 1 g a i n p=\dfrac{1}{gain} p=gain1
丢包率超过该值,有效带宽将会以 p − 1 g a i n p-\dfrac{1}{gain} p−gain1的速度快速衰减。
现代网络中,丢包率超过 20 % 20\% 20%的链路很少见,在大多数情况下,BBR都能用 1.25 1.25 1.25的增益抵抗丢包损失。如果事先知道丢包率确实很高,可以增大 g a i n gain gain值。
那么CUBIC的那条曲线如何解释呢?
CUBIC是Loss based CCA,由于CUBIC本质上是Reno的优化,为了避免在三次曲线上比划微积分,这里以Reno为例进行推导。
Reno将丢包视为拥塞的信号,简化起见,设链路有且仅有一个queue buffer,其容量为 C C C,RTprop极短,因此可以忽略传播时延,RTT全部是排队时延。由于Reno的MD系数为 0.5 0.5 0.5,那么一个AIMD周期内,拥塞窗口 W W W将于 0.5 C 0.5C 0.5C开始执行AI过程,直到 W W W达到 C + 1 C+1 C+1,产生一个丢包。
因此,可以认为丢包率就是在一个AIMD周期内传输总量的倒数,接下来求AIMD周期中的传输总量,即求解下图中阴影部分面积:

设传输总量为 N N N,则:
N = ( 0.5 C ) 2 + 1 2 ( 0.5 C ) 2 = 0.375 C 2 N=(0.5C)^2+\dfrac{1}{2}(0.5C)^2=0.375C^2 N=(0.5C)2+21(0.5C)2=0.375C2
因此丢包率 p p p为:
p = 1 0.375 C 2 + 1 ≈ 1 0.375 C 2 p=\dfrac{1}{0.375C^2+1}\approx \dfrac{1}{0.375C^2} p=0.375C2+11≈0.375C21
从而解得 C C C的值:
C = 1 0.375 p C=\sqrt{\dfrac{1}{0.375p}} C=0.375p1
这意味着丢包率 p p p与buffer容量 C C C有明确的一一对应关系。
接下来求Reno的平均带宽。整个AIMD周期内一个RTT时间的平均发送量为:
N r o u n d = 0.5 C + C 2 = 0.75 C N_{round}=\dfrac{0.5C+C}{2}=0.75C Nround=20.5C+C=0.75C
那么带宽即为:
T = 0.75 C R T T T=\dfrac{0.75C}{RTT} T=RTT0.75C
将上述的 C C C带入,即:
T = 0.75 R T T 1 0.375 p T=\dfrac{0.75}{RTT}\sqrt{\dfrac{1}{0.375p}} T=RTT0.750.375p1
这就是Loss based CCA的response function,详细情况请看:
https://blog.csdn.net/dog250/article/details/113874204
有了有效带宽 T T T和丢包率 p p p的关系,在RTT固定的情况下,我们看下 T T T- p p p曲线的走势:

和本文最初的图是吻合的,丢包率会极大影响有效带宽。
对于Loss based CCA的假设而言,丢包率唯一受queue buffer大小的影响,deep buffer场景下,buffer溢出前发送的数据总量很大,丢包率越低,如果遭遇shadow buffer,那么Loss based CCA和BBR相比,必跪。
接下来看下deep buffer的情景。
BBR在deep buffer场景下似乎并无优势,直观看就是,deep buffer场景下Loss based CCA的一个AIMD周期太久,这期间queue buffer将不断被挤压。
BBR本身在和Loss based CCA coexist的时候,由于up probe增益无效,将会快速进入cwnd limited。关于该事件的建模分析,可以参考:
https://www.cs.cmu.edu/~rware/assets/pdf/ware-imc2019.pdf
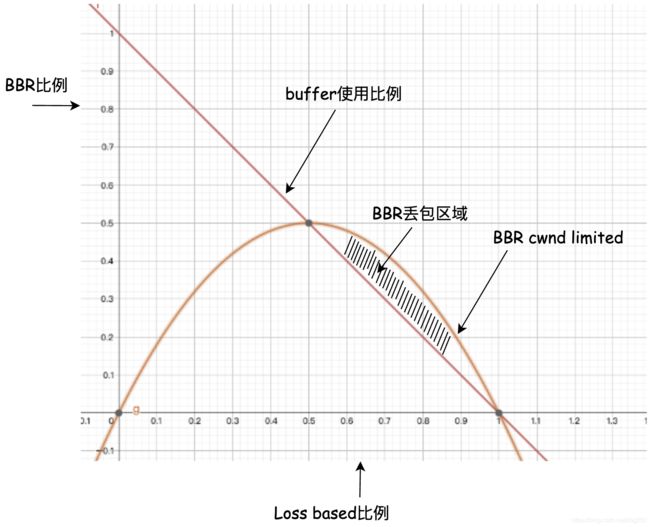
设queue buffer大小为1,BltBW为 B B B,其中Loss based流排队数据大小为 p p p,那么BBR可用的空间就是 1 − p 1-p 1−p。BBR的cwnd增益是2,cwnd的求法如下:
c w n d = 2 × B W m a x × R T T m i n cwnd=2\times BW_{max}\times RTT_{min} cwnd=2×BWmax×RTTmin
在上述场景下, B W m a x BW_{max} BWmax的值显然是:
B W m a x = ( 1 − p ) B BW_{max}=(1-p)B BWmax=(1−p)B
而此时的 R T T m i n RTT_{min} RTTmin显然是已经存在在Loss based流排队数据的出队时间:
R T T m i n = p B RTT_{min}=\dfrac{p}{B} RTTmin=Bp
带入上面cwnd表达式:
c w n d = 2 p ( 1 − p ) cwnd=2p(1-p) cwnd=2p(1−p)
可以看到,cwnd limited期间,BBR的cwnd会被限制在 0 0 0到 0.5 0.5 0.5个buffer之内,也就是说,BBR最多只能抢占一半的queue buffer,这便削弱了BBR和Loss based CCA coexist的时候抢占带宽的能力。
或许你会觉得把cwnd gain从2提升到4。很显然,这将导致阴影部分的增加,BBR将会产生更多的丢包。更合理的曲线是下面的蓝色曲线,极大值更高以允许发送更多包,曲线整体左边倾斜以缩小BBR丢包区域面积:

若希望在BBR发送端得到蓝色曲线描述的cwnd表达式,则需要能够用现有的测量量凑出这个曲线表达式。这一点我还没有深入思考。
似乎在deep buffer场景下,BBR全是劣势,然而这种劣势仅仅是理论上的,实验室结果。
在真实的现网环境中,特别是大RTT的长传场景,全链路的buffer远远不止1个,且buffer是串联的,只要有一个buffer是shadow buffer,溢出时间就以它为准,表象上整个链路就是shadow buffer的,按照概率相乘的原理,全链路全部都是deep buffer的概率特别低。因此很难出现上述理论分析中的结果。
除了buffer溢出丢包,还有很多噪声丢包,比如线路误码,信号衰减等等,Loss based CCA无法区分这些情况,它依然会假设buffer出现了溢出,进而执行MD。噪声丢包是随机的,时间越久丢包概率越大,因此RTT越大的场景,噪声丢包概率越大,其对Loss based流的影响也就越大。
好了,总结一下。
无论是全链路buffer串联,还是噪声随机丢包,Loss based CCA在deep buffer的优势都面临概率相乘的抵消,在空间上,所有的buffer全部是deep buffer的概率极低,在时间上,长时间不发生噪声随机丢包的概率极低。所有这些导致Loss based CCA未竟全功。
以上就是BBR为什么好的原因。特别是在长传场景,BBR的优势是碾压的。
我知道,肯定会有人抬杠称“我怎么试了下感觉BBR还没有CUBIC好…”诸如此类,在国内运营商环境,任何网络表现行为都可能出现,更何况BBR只是一个靠即时测量值试图自适应所有环境的CCA,怎么能指望它能cover住100%的场景呢?还是那句话,解决大部分问题就行了,至于那些点落零星,随他去吧。
至于魔改,我是反对的,调下参数可以,但不建议修改机制,我之前经常魔改CCA,结果都是狗熊掰棒子,甚至捡了芝麻丢了西瓜,当你看到哪里的机制有瑕疵时,看看别的地方,搞不好别的地方已经解决了。当今这么多CCA,都是经过理论推演和实际测试过了的,理论上任何魔改的效果都是负向的。以下两种情况下,可以魔改:
- 问题非常明确。
- 为了完成KPI。
浙江温州皮鞋湿,下雨进水不会胖。