一文搞定Plotly绘制面积图和直方图
面积图简介!
面积图又称区域图,强调数量随时间而变化的程度,也可用于引起人们对总值趋势的注意。堆积面积图和百分比堆积面积图还可以显示部分与整体的关系。
使用Plotly绘制面积图的方法与绘制折线图与散点图和折线图的方法相同,都是使用Scatter函数,不同之处在于fill参数的设置,fill=None表示无填充效果,使用mode属性可以隐藏面积图的边界线。在绘制堆积面积图时是不需要设置stack模式的,这一点就是堆积数据图需要累加数据,在本质上图的堆积效果是在同一个图形中绘制多个面积图。此外还可以对折现和坐标轴进行设置。
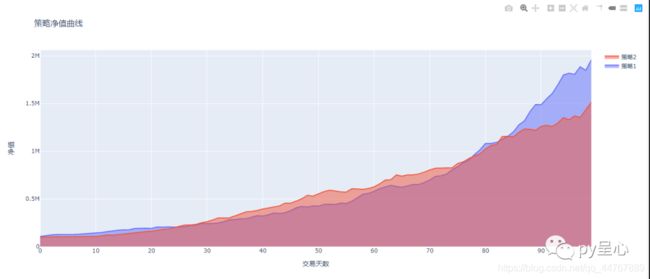
基本面积图!
代码实现!
import plotly as py
import plotly.graph_objs as go
import numpy as np
pyplt = py.offline.plot
#随机生成100个交易日的收益率
s1 = np.random.RandomState(8) # 定义局部种子
s2 = np.random.RandomState(9) # 定义局部种子
rd1 = s1.rand(100)/10 - 0.02
rd2 = s2.rand(100)/10 - 0.02
#设定初始资金
initial1 = 100000
initial2 = 100000
total1 = []
total2 = []
for i in range(len(rd1)):
initial1 = initial1*rd1[i] + initial1
initial2 = initial2*rd2[i] + initial2
total1.append(initial1)
total2.append(initial2)
trace1 = go.Scatter(
y = total1,
fill = 'tonexty',
mode= 'lines', # none,无边界线
name = "策略1"
)
trace2 = go.Scatter(
y = total2,
fill = 'tozeroy',
mode= 'lines',# 无边界线
name = "策略2"
)
data = [trace1, trace2]
layout = dict(title = '策略净值曲线',
xaxis = dict(title = '交易天数'),
yaxis = dict(title = '净值'),
)
fig = dict(data = data, layout = layout)
pyplt(fig, filename='temp/basic-area1.html')
效果截图!
内部填充面积图!
代码实现!
import plotly as py
import plotly.graph_objs as go
import numpy as np
# Interior Filling for Area Chart
pyplt = py.offline.plot
# 随机生成100个交易日的收益率
s1 = np.random.RandomState(8) # 定义局部种子
s2 = np.random.RandomState(9) # 定义局部种子
rd1 = s1.rand(100)/10 - 0.02
rd2 = s2.rand(100)/10 - 0.02
# 设定初始资金
initial1 = 100000
initial2 = 100000
total1 = []
total2 = []
for i in range(len(rd1)):
initial1 = initial1*rd1[i] + initial1
initial2 = initial2*rd2[i] + initial2
total1.append(initial1)
total2.append(initial2)
trace1 = go.Scatter(
# x = [1, 2, 3, 4],
y = total1,
fill = None,
mode= 'lines', # 无边界线
name = "策略1"
)
trace2 = go.Scatter(
# x = [1, 2, 3, 4],
y = total2,
fill = 'tonexty',
mode= 'lines',# 无边界线
name = "策略2"
)
data = [trace1, trace2]
layout = dict(title = '策略净值曲线',
xaxis = dict(title = '交易天数'),
yaxis = dict(title = '净值'),
)
fig = dict(data = data, layout = layout)
pyplt(fig, filename='temp/basic-area2.html')
效果截图!
堆积面积图!
代码实现!
import plotly as py
import plotly.graph_objs as go
pyplt=py.offline.plot
# Data
data_1 = go.Scatter(
x = ['基金1', '基金2', '基金3', '基金4','基金5'],
y = [32.52, 43.12, 43.47, 44.36, 33.11],
name = '股票投资',
mode = 'lines',
line = dict(width=0.5,
color = 'rgb(184, 247, 212)'),
fill = 'tonexty'
)
data_2 = go.Scatter(
x = ['基金1', '基金2', '基金3', '基金4','基金5'],
y = [63.24, 54.33, 74.28, 63.91, 63.11],
name = '其它投资',
mode = 'lines',
line = dict(width=0.5,
color = 'rgb(111, 231, 219)'),
fill = 'tonexty'
)
data_3 = go.Scatter(
x = ['基金1', '基金2', '基金3', '基金4','基金5'],
y = [83.24, 74.33, 93.91, 79.22, 83.11],
name='债券投资',
mode='lines',
line=dict(width=0.5,
color='rgb(127, 166, 238)'),
fill='tonexty'
)
data_4 = go.Scatter(
x = ['基金1', '基金2', '基金3', '基金4','基金5'],
y = [100, 100, 100, 100, 100],
name='银行存款',
mode='lines',
line=dict(width=0.5,
color='rgb(131, 90, 241)'),
fill='tonexty'
)
data = [data_1, data_2, data_3, data_4]
# Layout
layout = go.Layout(
title = '基金资产配置比例图',
showlegend = True,
xaxis = dict(
type = 'category',
),
yaxis = dict(
type = 'linear',
range = [1, 100],
dtick = 20,
ticksuffix = '%'
)
)
# Figure
fig = go.Figure(data = data, layout = layout)
pyplt(fig, filename = 'temp/stacked-area-plot.html')
效果截图!
直方图简介!
直方图,又称质量分布图,是一种统计报告图,由一系列高度不等的纵向条纹或线段表示数据分布的情况。一般用横轴表示数据类型,纵轴表示分布情况。
在质量管理中,如何预测并监控产品质量状况?如何对质量波动进行分析?直方图就是一目了然地把这些问题图表化处理的工具。它通过对收集到的貌似无序的数据进行处理,来反映产品质量的分布情况,判断和预测产品质量及不合格率。
直方图又称质量分布图,它是表示资料变化情况的一种主要工具。用直方图可以解析出资料的规则性,比较直观地看出产品质量特性的分布状态,对于资料分布状况一目了然,便于判断其总体质量分布情况。
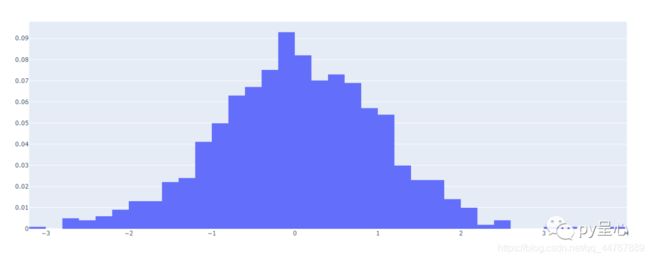
基本直方图!
使用Plotly绘制直方图需要用到graph_objs包中的Histogram函数。将数据赋值给函数中的x,就可以绘制直方图。若将数据赋值给y则可以绘制水平直方图。histnorm是Histogram函数的另一个属性,默认状态下表示直方图的纵坐标落入区间内的样本数量;若设定histnorm=‘probability’,则纵坐标变为落入区间内的样本频率。
代码实现!
import plotly as py
import plotly.graph_objs as go
import numpy as np
pyplt=py.offline.plot
s1=np.random.RandomState(1)
x=s1.randn(1000)
data=[go.Histogram(x=x,histnorm='probability')]
#y=x,表示水平直方图,histnorm='probability',y轴显示概率,没有则显示数目
pyplt(data,filename='temp/基本直方图.html')
效果截图!
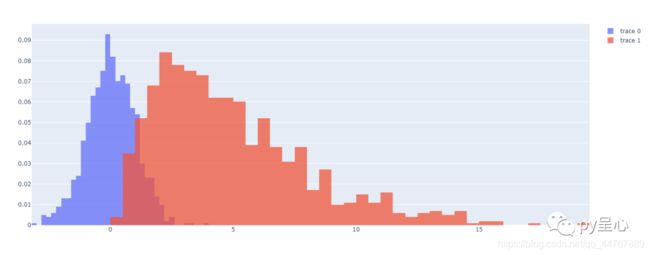
重叠直方图与层叠直方图!
在绘制重叠直方图时需要在Layout中设置barmode属性,将其改为’overlay’,在绘制层叠直方图时,需要将其设置为’stack’,如果不对其进行设置,会出现Plotly默认将两个直方图的柱状宽度强制变窄,以满足重叠部分显示的需要。通过Numpy正态分布数据和卡方分布数据。
代码实现!
import plotly as py
import plotly.graph_objs as go
import numpy as np
pyplt=py.offline.plot
s1=np.random.RandomState(1)
x0=s1.randn(1000)
x1=s1.chisquare(5,1000)
trace1=go.Histogram(
x=x0,
histnorm='probability',
opacity=0.75
)
trace2=go.Histogram(
x=x1,
histnorm='probability',
opacity=0.75
)
data=[trace1,trace2]
layout=go.Layout(barmode='overlay')
fig=go.Figure(data=data,layout=layout)
pyplt(fig,filename='temp/基本直方图2.html')
效果截图
import plotly as py
import plotly.graph_objs as go
import numpy as np
pyplt=py.offline.plot
s1=np.random.RandomState(1)
x0=s1.randn(1000)
x1=s1.randn(1000)
trace0=go.Histogram(
x=x0
)
trace1=go.Histogram(
x=x1
)
data=[trace0,trace1]
layout=go.Layout(barmode='stack')
fig=go.Figure(data=data,layout=layout)
pyplt(fig,filename='temp/基本直方图3.html')
效果截图!
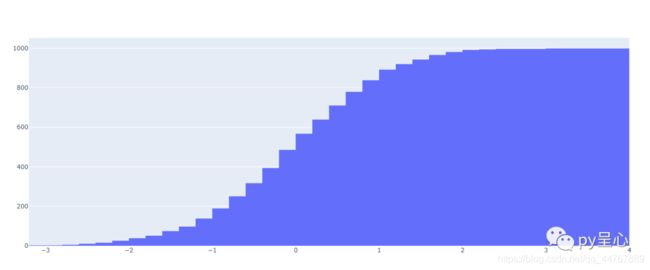
累积直方图!
累积直方图时直方图的累积形式,即第n+1个区间展示的数目是第n-1个区间的展示数目与第n个区间中实际样本数目之和,通过设置Histogram函数中的cumulative属性实现,即cumulative=dict(enabled=True).
代码实现!
import plotly as py
import plotly.graph_objs as go
import numpy as np
pyplt=py.offline.plot
s1=np.random.RandomState(1)
x1=s1.randn(1000)
trace1=[go.Histogram(x=x1,cumulative=dict(enabled=True))]
pyplt(trace1,filename='temp/基本直方图4.html')
效果截图!
综合应用!
plotly.figure_factoryly.figure_factory包中的displot函数将直方图与核函数估计可视化融合在一起,只需要将数据传给displot函数,即可完成相应的绘图。
代码实现!
import plotly as py
import plotly.graph_objs as go
import numpy as np
import plotly.figure_factory as ff
pyolt=py.offline.plot
#添加直方图数据
s1=np.random.RandomState(12)
#柯西分布
x1=s1.standard_cauchy(200)-4
#泊松分布
x2=s1.uniform(1,10,200)
#Gamma分布
x3=s1.standard_gamma(3,200)+4
#指数分布
x4=s1.exponential(3,200)+8
#数据组
hist_data=[x1,x2,x3,x4]
group_labels=['Group 1','Group 2','Group 3','Group 4']
fig=ff.create_distplot(hist_data,group_labels,bin_size=0.4)
pyolt(fig,filename='temp/直方图应用.html')
效果截图!
反思总结!
- 在学习的过程中需要学会逆向思维,使用逆向思维学的才快效果也会更加。
- 不能因为一处不懂就停留在那。看代码,记代码的效果远没有打一遍好。
- 当打代码的速度提高了后,学习的效率也接着提高。