DBSCAN 聚类 Matlab 可视化 实现
机器学习算法之:DBSCAN 聚类 MATLAB 可视化实现
DBSCAN介绍
DBSCAN( Density-Based Spatial Clustering of Applications with Noise ) 是一种比较有代表性的基于密度的聚类(Density-based clustering)模型,即通过样本分布的紧密程度来对样本进行分类。
- 一些术语
簇: 在DBSCAN中,将簇描述为密度相连的最大点集,即通过样本密度,将相对紧密的点集划分成为一个簇。
E-邻域: 所谓E-邻域,就是对于样本点周围以E为半径的区域。
核心点: 稠密区域内部的点,在该点半径为E的区域,样本点超过MinPts的点。
边界点: 稠密区域边界上的点,在该点E-邻域内,样本点小于MinPts的点,但该点为核心点的邻居。
噪声点: 稀疏区域中的点,除上面的点外的点。
直接密度可达: 如果p为q的E-邻域内,且q为一个核心点,
密度可达: 对于一串样本点满足p = p1 – p2 – p3 – … – pn = q (–代表直接密度可达) ,则称p与q密度可达。(相当于同一条链路的两个样本点)
密度相连: 如果关于样本O为 p, q 关于E-邻域以及MinPts的密度可达,则称p与q是密度相连的。(相当于分叉链路中处于交点周围点的关系)
-算法思路
伪代码:
标记所有样本点为unvisited;
while(随机选择一个unvisited样本点m,直到没有unvisited样本点)
{
m = visited;
if(m的E-邻域的样本点个数>=MinPts)
{
创建新簇Sm,并将m添加到Sm;
将m的E-邻域样本点放入集合N中;
for(每个样本n in N)
{
if(n==unvisited)
{
n = visited;
if(n的E-邻域的样本点个数 >= MinPts)
将这些对象添加到N中;
if(n不是任何簇的成员)
将n添加到N;
}
}
输出Sm;
}
else
标记m为噪声;
}DBSCAN动态MATLAB展示
下面是DBSCAN的动态演示Matlab代码
%% DBSCAN: A kind of density-based clustering algorithm
% INPUT: D: A data set contains n objects. ?: Radius. M: Density threshold for neighborhood
% Reference: wenku.baidu.com/view/e823e12ee2bd960590c677d6.html
function DBSCAN
% Clear variables, etc..
clear;
close all;
clc;
%%
% Initialize data sets ( data1 data2 data3 )
n = 200; % The first and second data sets
a = linspace(0,8*pi,n/2); % Set the values for x
%u = [1.2*a.*cos(a) 1.2*(a+pi).*cos(a)]'+0.1*rand(n,1);
%v = [1.2*a.*sin(a) 1.2*(a+pi).*sin(a)]'+0.1*rand(n,1);
u = [5*cos(a)+5 10*cos(a)+5]'+1*rand(n,1);
v = [5*sin(a)+5 10*sin(a)+5]'+1*rand(n,1);
% The third data set - Gaussian distribution
mu1 = [20 20]; % The first data set
S1 = [2 0;0 2]; % Co-variance matrix
data1 = mvnrnd(mu1,S1,100); % Generate the gaussian distribution data set 3
data = [u v;data1]; % Combine these three data sets together
%figure(1); % Draw these data in figure1
%plot(data(1:100,1),data(1:100,2),'b*'); % The first data set
%hold on
%plot(data(101:200,1),data(101:200,2),'r*'); % The second data set
%plot(data(201:300,1),data(201:300,2),'g*'); % The third data set
%hold off
image = imread('1.png');
disp(image);
[x,y]=find(image == 1);
data=[x,y];
dbscan(data,3,0.2); % random_data
%dbscan(data,3,0.004); % 2.png
%dbscan(data,3,0.2); % 1.png
%dbscan(data,3,0.02); % 1.png
end
%% DBSCAN function parameters
% Input: data (m,n), m objects n variables
% k number of objects in a neighborhood of an object
% (minimum number of object in a neighborhood of an object)
% Eps - neighborhood radius
% Output: class - vector specifying assignment of the i-th object
% type - vector specifying type of the i-th object
% (core:1, border:0, outlier:-1)
% Reference: http://www.chemometria.us.edu.pl
function [class,type,clusteridx]=dbscan(data,k,Eps)
x=zscore(data); % Standarlize
[m,~] = size(data);
if nargin<3||isempty(Eps)
[Eps]=epsilon(x,k);
end
x=[(1:m)',x]; % Add the serial number
[m,n] = size(x); % Reobtain the row and column
type = zeros(1,m); % Initialize the type values
no = 1; % The serial number of current cluster
touched = zeros(m,1); % whether this object is scanned
class = zeros(1,m)-2;
% Draw the initial scaled data set
figure(2);
plot(x(:,2),x(:,3),'k.');
xlabel('x');ylabel('y');
title('Predict data by using DBSCAN');
hold on;
color1 = [rand(),rand(),rand()];
color2 = [rand(),rand(),rand()];
for i = 1:m % Traverse the whole data set
if touched(i) == 0 % if this object is not scaned
ob = x(i,:); % Obtain the current object
%D=dist(ob(2:n), x(:,2:n)); % Calculate the Euclidean distance
%ind = find(D <= Eps); % Obtain the number of neighbor
ind=kdtree(x(:,2:n),ob(2:n),Eps);
if(length(ind) > 1 && length(ind) < k+1); % Border point
type(i) = 0; % Border point: 0
class(i) = 0;
end
if(length(ind)==1) % Outlier point
type(i) = -1; % Outlier point: -1
class(i) = -1;
touched(i)=1; % Ignore this value in later scaning process
end
if(length(ind)>=k+1) % Core point
type(i)=1; % Core point: 1
class(ind)=ones(length(ind),1)*max(no); % Assign class to the border points
figure(2)
draw(x,no,ind,color1) % draw the core point
h=circle(x,Eps,i);
draw(x,4,i,color2) % draw the border points
%pause(0.00001) % pause
drawnow;
delete(h);
color1 = [rand(),rand(),rand()];
color2= [rand(),rand(),rand()];
while ~isempty(ind) % iteration
ob = x(ind(1),:); % Check whether the border points is core points
touched(ind(1))=1; % Set status scanned
ind(1)=[]; % remove the current point
%D = dist(ob(2:n),x(:,2:n)); % calculate the distance between the the current point with neighbor points
%i1=find(D<=Eps); % return required points
i1=kdtree(x(:,2:n),ob(2:n),Eps);
if length(i1)>1 % if this point is not a noise point
class(i1)=no; % set the label to the current label
if length(i1)>=k+1; % If this point is a core point
type(ob(1))=1; % Set the type with 1
else % Border point
type(ob(1))=0; % Set the type with 1
end
figure(2)
draw(x,no,i1,color1) % Draw the border point
draw(ob,4,1,color2) % Draw the core point
h=circle(ob,Eps,1);
%pause(0.00001) % Pause
drawnow;
delete(h)
figure(2)
draw(ob,no,1,color1) % Draw the core point with label
for k1=1:length(i1)
if touched(i1(k1))==0 % If this point has neighbor points
touched(i1(k1))=1; % Set status scanned
ind=[ind,i1(k1)]; % Append this points to index for latter scanning process
class(i1(k1))=no; % Set the label to the current label
end
end
end
end
no = no+1; % Add one
end
end
end
i1=find(class==0); % If there are some points left
class(i1)=-1; % Set label to -1
type(i1)=-1; % Set type to 1;
maxlab = max(class); % Obtain the maximum label
clusteridx=[]; % The points in the clusters
clun=[]; % The number of points in every cluster
for ck=1:maxlab
tidx=find(class==ck);
clusteridx=[clusteridx;[tidx,zeros(1,m-length(tidx))]];
%clusteridx=[clusteridx;tidx]; % The points' serial number in every cluster
clun=[clun,length(tidx)]; % The number of points in evert cluster
end
disp(clun);
hold off
end
function [D] = dist(i,x)
[m,~] = size(x);
D = sqrt(sum((ones(m,1)*i-x).^2'));
end
function [Eps] = epsilon(x,k)
[m,n] = size(x);
Eps=((prod(max(x)-min(x))*k*gamma(.5*n+1))/(m*sqrt(pi.^n))).^(1/n);
disp('Eps');
disp(Eps);
end
function draw(data,no,i,color)
plot(data(i,2),data(i,3),'*','Color',color,'MarkerFaceColor',color);
end
function [h]=circle(data,R,i)
alpha=0:pi/50:2*pi;%角度[0,2*pi]
%R=2;%半径
x=R*cos(alpha)+data(i,2);
y=R*sin(alpha)+data(i,3);
h=patch(x,y,'r','edgecolor','none','facealpha',0.2)
%h = plot(x,y,'r-');
%axis equal;
%axis off
%set(gcf,'color','w');
end
function [ret]=kdtree(data,obj,r)
%Mdl = createns(X,'NSMethod','kdtree','Distance','euclidean');
%IdxNN = knnsearch(Mdl,Q,'K',5);
MdlKDT = KDTreeSearcher(data);
% r-Search radius
IdxKDT = rangesearch(MdlKDT,obj,r); % Cell
ret = IdxKDT{1};
end
下面是测试所用图片下载链接.
下图为DBSCAN的动态展示:
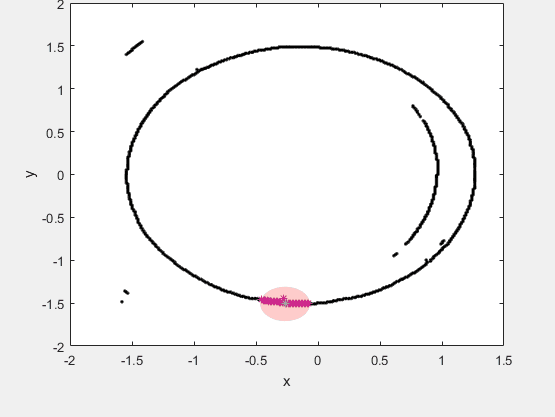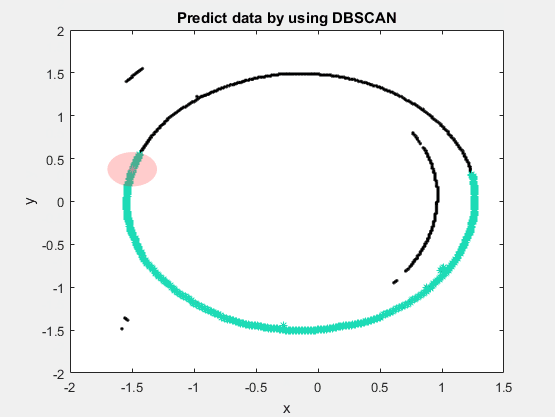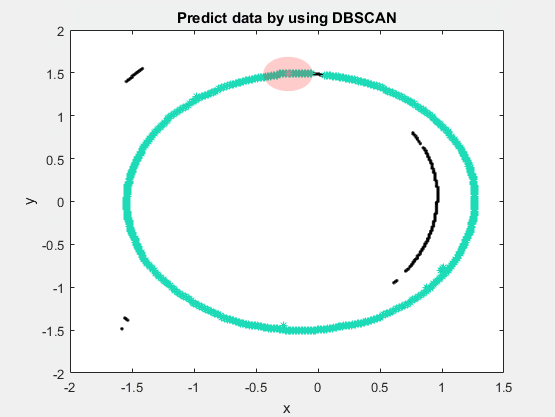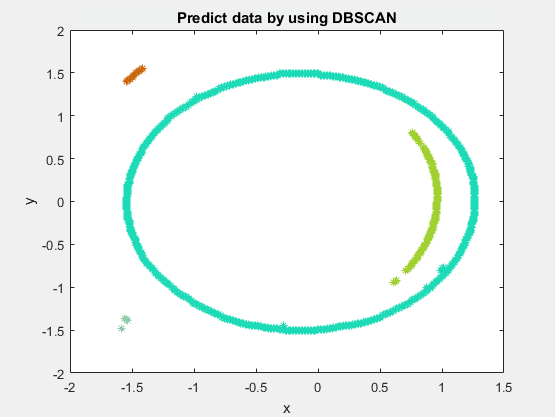
DBSCAN的优点
- 不需要事先设置簇的数量
- 可以通过密度,形成不同形状的簇
- 能够识别噪声点
- 对于样本输入顺序不敏感
- 同时克服基于距离聚类算法只能发现"类圆"聚类的缺点
DBSCAN的缺点
- 不能很好的反应高维数据
- 不能很好反映数据集变化的密度
- 对于密度不均,聚类间差大的样本,聚类质量不佳
Reference
https://baike.baidu.com/item/DBSCAN/4864716?fr=aladdin
https://wenku.baidu.com/view/ce3e324aa8956bec0975e3d5.html?sxts=1562940365069&sxts=1562982214479
wenku.baidu.com/view/e823e12ee2bd960590c677d6.html