linux 浮点异常,浮点数学函数异常处理方法

无论是解决素数分布问题的基础科学、实现全球天气预报的应用科学、验证导弹飞行实验的工程项目,还是日常生活中一张图片的显示(依赖于余弦变换)、一个通信的建立(依赖于语音采样)都离不开浮点计算,而对于计算而言,最基本的要求就是其结果的绝对正确性,但这个基本要求在计算机系统中很难得到保证.目前,科学计算大多使用浮点硬件,且都遵循IEEE-754浮点标准[,此标准定义的浮点数在数轴上呈离散态,在计算过程中需要对计算结果进行近似表示,而计算总是伴随着舍入,增加了浮点不精确甚至异常的可能.例如:由于浮点数转整数出现的整数溢出异常,欧洲Ariane 5火箭在1996年发射时出现了严重的升空自爆现象[,造成了巨额的经济损失.2010年,由于控制软件异常导致的丰田汽车刹车问题,同样给个人带来了极大的安全隐患[.这些事件都表明了浮点数计算异常的危害性及其难以控制性.此外,即使没有浮点计算异常,在常规计算中也可能出现非常规情况,即所谓的病态条件[,如文献[中的函数:

$f(x) = \frac{{\tan (\sin (x)) - \sin (\tan (x))}}{{{x^7}}}.$

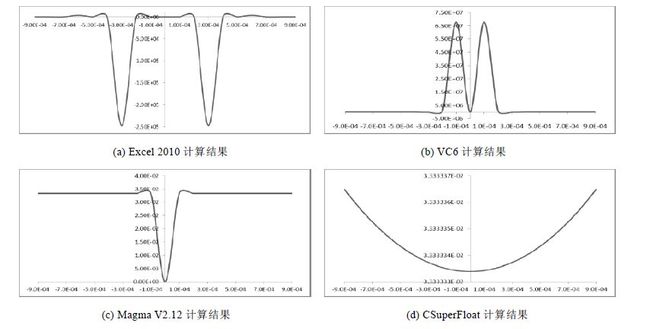
该函数在x=0.0处的真值为1/30,而利用4种不同计算软件计算的结果却存在较大差异,如图1所示.

图1(Fig.1)

图1

4种软件计算结果

Fig.1

Four software calculation results

通过不同的计算方法计算函数在x=0.0附近的函数值,不同的方法呈现出了不同的计算结果:

· 利用Excel 2010,Magma V2.12和VC6软件计算的结果都出现了大幅度的波动,并且x=0.0处函数值为0.0;

· 利用CSuperFloat软件计算的结果则比较平滑,一直在3.333333E-02附近渐变,且0.0处的值为3.333333383E-02,非常接近真值[.

这就是浮点计算的特点,在计算精度有限的情况下,计算方法的不同将可能导致计算结果的多样性.要想获得准确的计算结果,只能通过使用更高精度的计算方法实现.然而无论采用什么样的计算方法、设置多高的精度,都避免不了异常对计算的干扰,只有有效控制并处理好异常,才能确保计算的精确性,提高软件的可靠性.

当然,实现一个不会产生浮点异常的数值计算软件是异常困难的[,至今一直有很多学者致力于软件的可靠性、函数异常等相关领域的研究.从整个软件的可靠性角度出发,基于形式化分析实现的软件测试及验证工具[,在证明系统中将IEEE浮点标准形式化的工具Coq,Gappa等

另一方面,从具体的异常角度出发,Hong等人[对浮点数参与四则运算时的异常状况做了详细的分析,根据运算规则给出了无穷数参与运算后的返回值,为浮点计算软件的异常分析提供了支持.而对于浮点计算软件的异常研究,自Goodenough[将异常处理方法进行符号化、Cristian[成功实现应用后,其基本原理就没有发生大的变化.但还是有很多研究人员致力于这方面的研究,他们试图在新的语言或新的应用环境下获得更有效的异常处理方式,Garcia[,Gabral等人[对这类研究进行了详尽的对比分析.这些研究都具有一个共同的特点,都是基于C++.Java等面向对象语言实现.

除此之外,能够对异常处理起到指导作用的异常检测方面的研究也在蓬勃发展中,特别是对整数溢出的研究.如:基于动态检测技术,通过检测所有可能产生溢出的操作而实现的RICH工具[,卢锡城提出一种二进制高危整数溢出错误的全自动测试方法DAIDT[;基于静态区间分析,利用future bounds对变量进行处理的整数溢出分析算法[.诸多研究都在不断地提高着软件的可靠性.

虽然针对异常的研究很多,但目前的研究都存在一定的局限性:首先,现有的方法不针对浮点函数设计,且浮点函数以浮点运算为核心;其次,浮点函数使用汇编语言实现,现有的方法并不针对汇编;最后,现有方法的研究重点都集中在整数溢出错误上,而浮点函数的运算降低了整数溢出存在的可能.上述因素造成了当前研究成果直接在基础浮点函数中应用的局限性.

基础浮点函数最大的特点就是高效性,如何在保证函数运行高效的基础上实现高可靠的异常处理机制,是本文面临的最大挑战之一.围绕这一挑战,本文利用寄存器运算快的特点实现了浮点异常的编码;利用浮点函数计算集中的特点实现了基于核心运算隔离技术的分段式异常处理方法.该方法以准确处理各类异常为首要目标,并辅以将异常处理对函数性能的干扰降到最低的要求,充分利用各类异常伴随的错误码不同、可能触发的位置不同、触发条件不同的特点,围绕核心运算,将异常分为3个阶段进行处理:输入参数处理阶段,通过对输入参数的检测,保证进入核心运算的参数不会触发INV异常;特定代码检测阶段,在核心运算执行过程中检测并处理可能出现的DZE异常和INF异常;输出结果处理阶段,在核心运算后检测可能出现的FPF异常和DNO异常.由于在机器中的浮点数的存储是离散的,无法与实数一一对应,这使得浮点计算总是面临着舍入,所以在浮点函数的计算过程中INE异常几乎无处不在.因此在一般情况下,该异常总是处于屏蔽状态.就作者目前的了解,这是第一个针对汇编语言实现的,基于核心运算隔离的分段式浮点函数异常处理方法.分段式处理能够有效降低实现的难度,降低异常处理对函数性能的干扰.

本文的主要贡献:

· 实现浮点函数异常的编码,将各类异常与浮点数相对应,利用寄存器运算快的特点,提高了异常处理的效率;

· 提出一种适用于浮点函数的分段式异常处理方法,实现了异常处理与核心运算的分离,降低了异常处理过程对函数性能的干扰,为类似软件的异常处理提供了新的方法,并成功应用于608个浮点函数中;

· 对新的异常处理方法的依据做了详尽的理论论证,为基于核心运算隔离的分段式异常处理方法在新的语言及环境中的扩展提供了可能.

为了更加清晰地描述本文的问题,在第1节对浮点函数的异常类型做了详尽的阐述.在此基础上,第2节给出了整体的异常处理算法和异常处理方法有效性的理论论证及其重要的子算法,包括浮点函数异常编码、输入参数处理、特定代码检测、输出结果处理和异常返回.最后,利用第3节和第4节,分别对异常处理方法进行了测试分析和总结.

1. 浮点异常类型

浮点计算并不封闭,经常出现各类异常[.IEEE-754标准分别对各类异常进行了定义[,分别是参数不符合输入要求的无效操作异常(invalid operation exception,简称INV)、除零异常(dividing by zero exception,简称DZE)、浮点溢出异常(floating-point flow exception,简称FPF)和不精确异常(inexact exception,简称INE).对于一般意义上的浮点计算,可能出现的异常状况都在IEEE-754标准定义的异常范围之内;但对于本文研究的浮点函数(主要包括由一系列浮点计算实现的三角类函数、指数类函数等初等函数[),由于其计算的复杂性以及对计算高可靠的要求,还包含以下两种异常:非规格化数异常(denormal operand exception,简称DNO)和整数溢出异常(integer flow exception,简称INF).

为了更好地理解浮点异常,有必要先了解浮点数的分类和特性.浮点函数的实现采用的是IEEE-754标准的浮点数表示形式.IEEE-754定义了一些特殊值以提高特殊情形下的处理能力,而这些特殊值却是浮点异常被触发的最大根源.IEEE-754标准通过指数将浮点表示空间划分成5类数:非数(not a number,简称NaN)、无穷数(inf)、有限数、零和非规格化数(denormal floating-point,简称dnp).

NaN是为了方便而提出的一种表示方法,其指数部分是最大值,隐含位(也叫整数位)是1,但尾数部分不是0.NaN有两类:一类是QNaN(quiet NaN),一般表示未定义的算术运算结果;一类是SNaN(signal NaN),一般被用于标记未初始化的值,两者均能触发异常.

浮点函数在实现过程中可能面临多种异常类型,其中,每一类异常又可能存在多种表现形式,触发的条件、返回的错误码等都有不同的呈现.

INV异常包括:由输入参数类型不匹配(如将双精度数x作为参数传给单精度函数float sqrtf(float x))而引起的参数类型不匹配异常;由输入的参数值超过其参数域范围(如将负数x作为参数传给定义域为[0,+¥)的双精度函数double sqrt(double x))而引起的参数值不匹配异常;由传递空指针(如调用函数double frexp(double x,int *ip)时,ip为空值)或无法访问传递的指针所指向的地址(如指针ip指向的缓存,在调用frexp()函数前已经被释放)而引起的传递无效指针异常.INV异常的产生也可以归纳为:若当前操作的一个操作数为非有限数或对要执行的操作而言是非法的,则触发INV异常,包括:1) (+¥)+(-¥);2) 0x¥;3) 0/0;4) ¥/¥;5) sqrt(-2,0);6) NaNex等,其中,¥为无穷数,e为四则运算,x为任意浮点数.

FPF异常包括由计算结果超出浮点数可表示的最大数MAX(单精度±3.4028234663852886E+38)而引起的上溢(overflow),由计算结果小于浮点数可表示的最小值MIN(单精度±1.1754943508222875E-38)而引起的下溢(underflow),如图2所示.

图2(Fig.2)

图2

浮点数溢出

Fig.2

Floating-Point overflow

需要注意的是,下溢不是一个严重问题,通常看作为机器0.

DZE异常为当除数为0而被除数为有限数时触发的异常,也泛指有限数运算导致无穷结果的异常,例如4.0/0.0,log(0,0)等.在浮点函数实际运算过程中,一般只被除法指令FDIVS/FDIVD触发.

INE异常为由操作数或计算结果的不精确表示触发的异常,不精确表示的主要原因是浮点格式的有效位数不足以容纳精确的计算结果,如除不尽、两个浮点数相乘等情况都会触发该异常.由于INE异常会在浮点运算中经常被触发,在一般情况下总是被屏蔽.

本文涉及的INF异常特指在浮点向整数(长字)转换的过程中,若舍入后的结果超出了整数范围所产生的异常,在浮点函数实际运算过程中可以限定为2条浮点指令:FCVTDL(双精度浮点转换为长字,取值范围-263~263-1)和FCVTLW(长字整数转换为字整数,取值范围-231~231-1).

若当前浮点操作的操作数中存在非规格化数,则触发DNO异常.

关于DNO异常的处理可以限定为以下情况:

1) 具有非规格化操作数的浮点指令不会产生上溢、下溢或非精确结果自陷;

2) 除以一个非规格化数根据不同情况可以作为DZE异常或INV异常;

3) 非规格化数乘以无穷大作为INV异常;

4) 对一个负的非规格化数求平方根将产生一个负0结果,而不产生异常;

5) 非规格化数被当作0,不会引起DNO的自陷;

6) 在浮点函数实际运算过程中,非规格化数多数被当作0.

上述6类异常都将会被最基本的浮点操作(加、减、乘、除)或浮点函数(sqrt,sin,pow,fp_class等)所触发.首先定义一个函数E:经过某一个运算(基本浮点操作或者浮点函数)后,可能出现的状态及其触发条件.对于浮点数OP1和OP2,经过E后有如下的规则:

$\begin{array}{l}

E(OP1\Theta OP2) = \left\{ {\begin{array}{*{20}{l}}

{Invalid,{\rm{ if }}(OP1{\rm{ or }}OP2) = = NaN{\rm{ or }}\inf }\\

{Overflow,{\rm{ if }}|OP1\Theta OP2| > {\rm{MAX}}}\\

{Underflow,{\rm{ if }}0 < |OP1\Theta OP2| < {\rm{MIN}}}\\

{Denormal,{\rm{ if }}0 < |OP1| < {\rm{MIN or }}0 < |OP2| < {\rm{MIN}}}\\

{OP1\Theta OP2,{\rm{ otherwise}}}

\end{array}} \right.,\Theta = \{ + , - , \times \} ,\\

E(OP1/OP2) = \left\{ {\begin{array}{*{20}{l}}

{Invalid,{\rm{ if }}((OP1{\rm{ or }}OP2) = = NaN{\rm{ or }}\inf ){\rm{ or }}(OP1 = 0{\rm{ and }}OP2 = 0)}\\

{Overflow,{\rm{ if }}|OP1| > \left| {OP2} \right| \cdot {\rm{MAX}}}\\

{Underflow,{\rm{ if }}0 < |OP1| < |OP2| \cdot {\rm{MIN}}}\\

{Denormal,{\rm{ if }}0 < |OP1| < {\rm{MIN or }}0 < |OP2| < {\rm{MIN}}}\\

{Divide{\rm{ }}by{\rm{ }}Zero,{\rm{ if }}(OP1 \ne 0{\rm{ or }}NaN{\rm{ or }}\inf ){\rm{ and }}OP2 = 0}\\

{OP1/OP2,{\rm{ otherwise}}}

\end{array}} \right..

\end{array}$

四则运算是浮点计算的基础运算,了解经过四则运算可能产生的各种异常,是后续对浮点函数异常分析的基础.虽然每个函数由于自身的功能不同,可能导致的异常有所不同,但回到本源都是由基本运算引起的异常.部分浮点函数异常状况如下:

$\begin{array}{l}

E(sqrt(OP1)) = \left\{ {\begin{array}{*{20}{l}}

{Invalid,{\rm{ if }}(OP1 < 0){\rm{ or }}(OP1 = = NaN{\rm{ or }}\inf )}\\

{z,{\rm{ and }}z \cdot z = x,{\rm{ otherwise}}}

\end{array}} \right.,\\

E(\sin (OP1)) = \left\{ {\begin{array}{*{20}{l}}

{Invalid,{\rm{ if }}OP1 = = NaN{\rm{ or }}\inf }\\

{z,{\rm{ otherwise}}}

\end{array}} \right.,\\

E(\cot (OP1)) = \left\{ {\begin{array}{*{20}{l}}

{Invalid,{\rm{ if }}OP1 = = NaN{\rm{ or }}\inf }\\

{Divide{\rm{ }}by{\rm{ }}Zero,{\rm{ if }}OP1 = 0}\\

{Overflow,{\rm{ if }}|OP1| \le 0x0003000000000000}\\

{z,{\rm{ otherwise}}}

\end{array}} \right.,\\

E(fp\_class(OP1)) = z.

\end{array}$

对于上述规则,函数和浮点操作可以相互嵌套,如E(sin(OP1/OP2)),E(sqrt(OP1)Qcot(OP1))等.无论是以何种方式嵌套出现,整体的E都是各子调用的并集,即:

E(sqrt(OP1)Qcot(OP1))=E(sqrt(OP1))ÈE(cot(OP1))ÈE(OP1QOP2).

2. 分段式异常处理

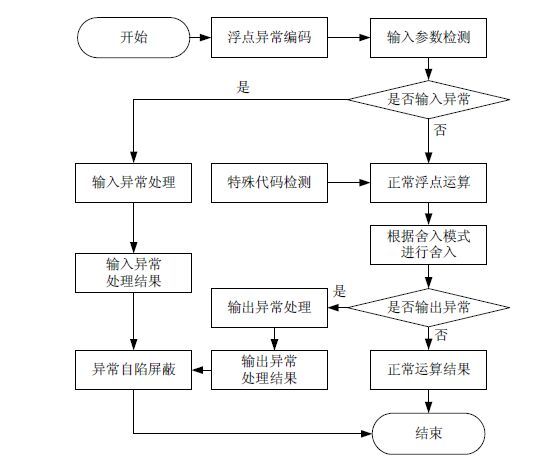
浮点函数的实现往往要兼顾3方面的需求:高可靠、高精度及高效率.而出于高效率的考虑,在异常处理方面往往采用静默模式,即:屏蔽所有异常,自我检测及处理.本文研究的异常处理方法起始于输入参数检测,终于输出结果检测,其基本流程如图3所示.

该处理流程在浮点函数实现之前完成对浮点异常的编码,将每一类异常编码为可表示的浮点数;在此基础上对输入参数进行异常检测,即,处理可能出现的INV异常;在正常运算的过程中,保持对浮点操作特殊指令的检测,将处理重点集中在INF异常和DZE异常;最后,对计算结果进行检测,处理可能存在的FPF异常和DNO异常.其具体算法见算法1.

图3(Fig.3)

图3

浮点函数异常处理方法流程图

Fig.3

Flow of floating-point function’s exception handling

算法1. ExceptionHandle:提供一个融合异常处理后的浮点函数算法,该算法分阶段对各类异常进行判断并处理.其中,COUNT_FDIV为核心运算中除法指令的个数,KeyCompute[i]为被除法指令分割开的各浮点函数子核心运算,Count统计核心运算未执行指令.其余相关变量的说明详见各子算法.

Inputs:任意浮点数构成的向量V=(p1,p2,p3,p4).

浮点函数F的定义域边界a,b;

F的参数类型pre;

F的参数个数num;

1. ExceptionCoding(E_code,E_type,E_pre,E_add); //算法2

2. if PartitionInputParameter(num,V,a,b) no INV then //算法3

3.   for 1,...,COUNT_FDIV do

4.     while check_INF()≠0 and Count(KeyCompute[i]())≠Æ do

5.     R=KeyCompute[i](R);

6.    end while

7.    if Count(KeyCompute())=Æ then

8.     if PartitionOutputParameter(R) no FPF then //算法5

9.      return R; goto 3; //return result

10.     else

11.      E=Exception(exc_num); //算法6

12.      return E; //return exception

13.     end if

14.    else

15.     E=Exception(exc_num);

16.     return E; //return exception

17.    end if

18.    if check_DZE()≠0 do

19.     E=Exception(exc_num);

20.     return E; //return exception

21.    end if

21.   end for

22. else

23.   E=Exception(exc_num);

24.   return E; //return exception

25. end if

实现一个完整的浮点函数,异常处理代码就占到整个代码的三分之二[,是实现过程中不可或缺的一部分.算法1在利用ExceptionCoding算法实现异常类型编码的基础上,根据不同的条件调用输入参数检测算法PartitionInputParameter、特定代码检测算法check_DZE和check_INF、输出结果检测算法PartitionOutput Parameter以及异常返回算法Exception.其中,由于除法指令在触发异常时的特殊性,本文利用除法指令将函数核心运算分成若干个子运算,这也是该算法分段处理的一个具体表现.所谓的核心运算指为实现函数功能而存在的计算密集型代码段,是函数的主体计算部分.

总体来看,本文异常处理方法的分段特点在算法1中体现在:核心运算前,利用算法的第2行、第22行~第25行进行INV异常的检测和处理;在核心运算中,利用算法第4行~第6行、第14行~第21行进行INF异常和DZE异常的检测和处理;在核心运算后,利用算法第8行~第13行进行FPF异常(包含了对DNO异常的处理)的检测和处理;除此之外,利用第3行对核心运算进行了拆分.

2.1 理论依据

上述异常处理方法最大的特点是分段实现,最大限度地降低了异常处理对核心运算的干扰.其有效性主要依靠两个重要的结论:(1) 非有限数(NaN和inf)参与运算依然为非有限数,这里的非有限数并不包括非规格化数;(2) 在运算过程中出现的非规格化数作为真零处理,只有最后的结果出现非规格化数才会真正触发DNO异常.正是由于两个结论,才使得本文可以将异常检测及处理集中在程序的两端(输入阶段和输出阶段)与中间的核心运算隔离开,保证计算的连贯性和高效性.

在对结论1进行论证前,首先关注如下的定义及运算规则,下述研究都在浮点数的背景之下进行.

定义1(机器可表示浮点数$\Re $). 由0、有限数和非有限数组成的全体集合,从逻辑上可以用三元组{s,e,m}表示,即n=(-1)sxmx2e-OFFSET.其中,s表示符号位,e是指数位,OFFSET是指数偏移,m是由隐含的整数位和小数f组成的尾数.

定义2(有限数$\psi $). 浮点数指数在最大值和最小值之间,且整数位恒为1的数.有限数的形式是(-1)sx(1+f)x 2e-OFFSET.其中,1是被隐含的整数位.

定义3(非有限数$\bar \Psi $). 除0和$\psi $之外的所有浮点数,包括inf,NaN和dnp.

定义4(狭义的非有限数$\hat \Psi $). 除非规格化数之外的所有$\hat \Psi $,包括inf和NaN.

运算规则1(浮点数加/减规则). (1) 零操作数检测;(2) 比较阶码大小并对阶;(3) 尾数加/减操作;(4) 结果规格化并进行舍入处理.

运算规则2(浮点数乘/除规则). (1) 零操作数检查;(2) 阶码加/减操作;(3) 尾数乘/除操作;(4) 结果规格化并进行舍入处理.

结论1. 狭义的非有限数参与加减乘运算后的运算结果必为非有限数,即$\hat \Psi \Theta \Re \bar \subset \bar \Psi ,\bar \subset $表示必属于.

对于结论1的证明,将分为NaN和inf两种情况.

首先,对于NaN而言,在数学上并没有相应的数或符号与之对应,NaN通常可以理解为非法操作的一种标识,所以有$NaN \odot \Psi \bar \subset NaN,NaN \odot dnp\bar \subset NaN,NaN \odot 0\bar \subset NaN$(不产生DZE异常)和$NaN \odot NaN\bar \subset NaN;$

虽然当NaN取任何值且出现$\sqrt {{\infty ^2} + Na{N^2}} $时,该公式的结果值为inf,但除了这种特殊情况,还是有$NaN \odot inf\bar \subset NaN$,所以无论特殊情况下结果为inf,还是一般情况下结果为NaN,都有$NaN \odot inf\bar \subset \bar \Psi .$

综合来看,有$NaN \odot \Re \bar \subset \bar \Psi $,亦有$NaN\Theta \Re \bar \subset \bar \Psi $.

其次,对于inf而言,先假设对于任意浮点数$x = {( - 1)^{{s_x}}} \cdot {2^{{E_x}}} \cdot {M_x},y = {( - 1)^{{s_y}}} \cdot {2^{{E_y}}} \cdot {M_y}$和z,不妨设Ex全1,My全0.即:假定y为inf,且x不为NaN.

对于加减法而言,由假设有Ex≤Ey,根据运算规则1,有$z = x + y = {( - 1)^{{s_z}}}{2^E}^{_y}({M_x}{2^{{E_x} - {E_y}}} \pm {M_y}).$

令$({M_x}{2^{{E_x} - {E_y}}} \pm {M_y}) = {M_z}$,则$z = {( - 1)^{{s_x} + {s_y}}}{M_z}{2^E}^{_y}$,即,浮点数z的指数依然全1.所以无论当Mz=0时z为inf,还是Mz≠0时z为NaN,都有$z\bar \subset \hat \Psi \bar \subset \bar \Psi .$

对于乘法而言,根据运算规则2,有$z = x \times y = {( - 1)^{{s_z}}}{2^{{E_x} + {E_y}}}({M_x} \times {M_y})$.由假设可知,无论Ex=0时Ez=Ex+Ey全1,还是Ex≠0时Ez超出可表示范围,都有$z\bar \subset \hat \Psi \bar \subset \bar \Psi $或z出现溢出.而当出现溢出时,同样可以表示为NaN,所以有$z\bar \subset \hat \Psi \bar \subset \bar \Psi .$.

综上所述,$\hat \Psi \Theta \Re \bar \subset \bar \Psi .$

结论2. 有限数与有限数进行四则运算后的结果可能为非规格化数,即$\Psi \odot \Psi \tilde \subset dnp,\tilde \subset $表示可能属于.

对于结论2,假设y$ \in $$\psi $,x=y+MIN,z=0.5,则经过(x-y)xz后的计算结果$r\bar \subset dnp$,且有x$ \in $$\psi $,(x-y)$ \in $$\psi $及z$ \in $$\psi $.

由上述假设可知:存在有限数经过某些运算后的运行结果为dnp,即$\Psi \odot \Psi \tilde \subset dnp.$

通过对结论1的证明,可以充分说明分段式异常处理的有效性,即,不会出现在核心运算过程中出现异常后在计算的输出阶段不被检测的情况.换言之,核心运算中一旦出现异常,必然会将异常一步步传递下去,直到运算结束或被检测.对结论2的证明说明输出阶段对DNO异常检测的必要性,虽然在核心运算过程中不触发DNO异常(出现dnp则补指或作为0处理,具体含义见第3.2节),但在最后的计算中还是可能产生dnp(结论2),并在输出阶段触发DNO异常.

2.2 浮点异常编码

当触发异常时,程序员不仅需要知道异常的类型,还需要知道该异常的错误码、异常返回值等,诸多信息需要在异常发生的同时准确而快速地获取并处理.对于性能要求较高的浮点函数而言,简单直接的判断已经无法满足其要求.而对于采用汇编语言并基于浮点运算实现的浮点函数,快速运算的最有效途径就是在寄存器中对浮点数进行操作.浮点函数中的异常种类繁多,让异常处理程序高效快速的判断出异常类型并做出合理的处理是浮点异常编码的首要目的.因此,本文将异常类型进行了64位浮点数编码,确保通过简单的数值运算能够快速地识别异常的诸多特性,是整个浮点函数异常处理方法得以正确高效运转的基石.

在编码的过程中,根据浮点数类型(单精度和双精度)的不同,编码也有所差异,其对应的算法如下:

算法2. ExceptionCoding:将各类异常类型编码为64位浮点数.

Inputs:E_code,错误码;

E_type,异常类型浮点函数F的定义域边界a,b;

E_pre,异常精度;

E_add,返回地址;

将64位浮点数看作由64个变量t0~t63组成的字符串,t0表示浮点数的第0位,依此类推,且初始时t0~t63均为0.

1. t0:判错误码.当错误码为EDOM时t0=0,否则t0=1.

2. t1~t6:判异常类型.当异常类型为INV时t1=1;当异常类型为DZE时t2=1;当异常类型为OVF时t3=1; 当异常类型为UNF时t4=1;当异常类型为INE时t5=1;当异常类型为DNO时t6=1.

3. t7:判返回地址.当t7=0时,表示特殊点编号的t8~t13位为返回点地址;否则,表示特殊点编号的t8~t13 位与t14~t17位作模2加操作后再作为返回点地址.

4. t8:判单双精度.当函数类型为双精度时t8=1;当函数类型为单精度时t8=0.

5. t8~t13,t14~t17:返回地址.

6. t63:异常总标识.t1~t6存在1,则t63=1,否则t63=0.

7. exc_num=t0 or (t1<<1) or (t2<<2) or … or (t63<<63);

8. return exc_num;

运行算法2实现异常类型编码,能够确保程序快速准确地判断异常类型并返回预设的异常结果.以双精度为例,经过ExceptionCoding算法后的异常编码如下:

异常标识

编码

EXC_INV_ZERO_EDOM

0x8000000000000502

EXC_INV_NANZERO_EDOM

0x8000000000004502

EXC_INV_NANINF_EDOM

0x8000000000019902

EXC_UNF_ZERO_ERANGE

0x8000000000000511

EXC_UNF_NINF_ERANGE

0x8000000000039909

EXC_DNO_DNO_ERANGE

0x8000000000000551

EXC_DZE_NINF_EDOM

0x8000000000039904

EXC_DZE_INF_EDOM

0x8000000000009504

EXC_OVF_INF_ERANGE

0x8000000000009509

EXC_ISIEEE

0xffffffffffffffff

其中,EXC_ISIEEE为特殊标识,当异常类型被设置为该标识时则直接返回,不对异常进行处理;EXC_INV_ ZERO_EDOM表示INV异常,返回值为0,且错误码为EDOM(源自于函式的参数超出范围);EXC_DNO_DNO_ ERANGE表示DNO异常,返回值为非规格化数,且错误码为ERANGE(源自于函式的结果超出范围).

2.3 输入参数检测

程序员在编程过程中,总是期望所有输入都不会引起程序的异常情况.但不幸的是:即使将输入参数小心地控制在函数定义域范围内,也可能触发一些异常(如DNO异常);幸运的是,该异常一般不会引起严重的后果.而当浮点数的特殊数参与浮点运算时,必然会引发浮点算术异常,从而使得函数运算过程中断,降低浮点函数的可靠性及性能.因此,在进入函数正常运算阶段前需要对函数的输入参数做特殊数检查:一方面将错误码为EDOM的异常解决在函数核心运算之前,另一方面确保函数核心运算的连贯性.

虽然不同的浮点函数在核心运算上有所不同,但却可以在函数的开始阶段对数据进行预判断,以区分输入参数的类型.本文利用比较指令对输入参数的判断进行统一的规范化操作,实现了输入参数检测子程序PartitionInputParameter.该程序的实现采用的是汇编语言,为了方便描述,转化成相应的C程序呈现.

算法3. PartitionInputParameter:实现输入参数的预判断,确保引起EDOM类异常的输入进入相应的异常处理子程序,其他则进入核心运算子程序.

Inputes:V,输入参数向量(p1,p2,p3,p4);

a,F定义域下界;

b,F定义域上界;

num,F的参数个数1~3;

MAX,无穷数;

VCPYF($1,$2):将寄存器$1中的浮点数扩展为向量并存入寄存器$2;VINSF($1,$2,$3):将$1中的浮点数插入到向量寄存器$2中的第$3个位置;CheckINFNAN(inf,V):检测向量V中是否存在无穷数或非数;CheckInterval(a,b,V):检测向量V中的变量是否在定义域区间内.

1. VCPYF(p1,V); //V=(p1,p1,p1,p1)

2. if num=2 then

3.   VINSF(p2,V,1); //V=(p1,p2,p1,p1)

4. else if num=3 then

5.   VINSF(p2,V,1);VINSF(p3,V,2); //V=(p1,p2,p3,p1)

6.  end if

7. end if

8. if CheckINFNAN(MAX,V)=TRUE then

9.  return INV;

10. else if CheckInterval(a,b,V)=TRUE then

11.   retuen INV;

12.  else

13.   return;

14.  end if

15. end if

PartitionInputParameter算法的贡献并不仅仅是实现了输入参数的检测这样一个功能,而是在实现的过程中结合SIMD编程思想,确保了算法的高效性,同时也实现了多参数函数的统一处理.程序中对SIMD的运用主要体现在向量V的构建.研究中发现:浮点函数的输入参数个数从1~3不等,输入参数的不确定性,增加了标量程序的工作量,如果使用标量运算,对于3个输入的函数而言,同样的判断则需要重复进行3次;而通过向量实现,则可以同时进行判断.通过实验分析可知:与标量实现相比,向量实现平均能有10%左右的性能提升.

2.4 特定代码检测

异常总是可能伴随着浮点函数运算存在,如随时都可能出现的溢出异常.如果在浮点运算过程中时时检测异常,必将严重影响运算效率.本文结合浮点函数实现过程中的特点,在浮点运算过程中并不对所有异常进行检测,只对由固定指令触发的DZE异常及INF异常进行检测,其余都交给运算结束后的输出结果检测子程序处理.本文通过对FDIVS(单精度除)和FDIVD(双精度除)指令的监控以处理可能出现的DZE异常,以及对FCVTDL (双精度浮点转换为长字)和FCVTLW(长字整数转换为字整数)指令的监控以处理可能出现的INF异常.

当前,对INF异常检测的研究尤为深入,大致可分为两类.

· 一类是动态检测技术.Brumley等人[通过对可能引起INF的每一个整数操作进行检测实现的C程序检测工具RICH,该工具最大的优势在于对程序性能干扰的控制,平均只有5%的性能下降;类似的方法还有Chinchani等人[的研究.Dietz等人[针对C/C++语言并从软件工程的角度实现的检测工具IOC,并发现了众多存在的INF,该工具并没有关注于对程序性能的影响;而Chen[实现的检测方法最大的缺陷就是造成程序性能下降了50倍;

· 另一类是静态检测技术.Molnar[利用符号执行实现了检测工具SmartFuzz;在此基础上,Wang[结合污点分析实现了检测工具IntScope.

上述研究都是针对面向对象语言实现,而浮点函数由汇编语言实现,加上DZE异常及INF异常出现位置固定且可能触发的次数有限,造成现有的检测方法在当前环境下无法发挥该有的优势.虽然相比较于其他学者的研究,本文的方法显得过于简单,但对于汇编实现的浮点函数,这样的方法确实是最准确有效的,能够在准确检测的同时最大限度地降低异常检测对函数整体性能的影响.通过统计发现:这两类指令在浮点函数中运用的比例都相对较小,对于FDIVS/FDIVD指令,只在152个函数中的28个函数中出现,并且在平均有上千行汇编代码的函数中最多出现次数也只有5次;对于FCVTDL/FCVTLW指令,只在15个函数中出现,最多出现次数也只有6次.

浮点函数中,DZE异常和INF异常的可能触发条件可以限定为上述4种指令的执行,而可能触发这两类异常的情况较少又决定了本节提出检测方法的有效性及高效性.具体而言,通过对指令FDIVS/FDIVD的搜索,实现核心运算中对DZE异常的检测;通过对指令FCVTDL/FCVTLW的搜索,实现核心运算中对INF异常的检测.

2.5 输出异常检测

为了保证核心运算的完整性,在浮点函数实现过程中并没有对FPF异常(DNO异常可以看作是FPF异常中的下溢)进行检测,而是将这部分工作统一放到了运算结束后.FPF异常的触发,可以转化为有限数运算结果为非有限数的情况.通过对运算结果的检测衡量函数是否出现异常,这样做基于第2.1节论证的两个结论.具体的输出异常检测算法如下.

算法5. PartitionOutputParameter:实现运算结果的FPF异常检测.

Inputs:R,核心运算结果;

a,F定义域下界;

b,F定义域上界;

num,F的参数个数1~3;

MAX,无穷数;

MIN,最小规格化数;

Checkoverflow(MAX,V):检测R是否出现上溢;Checkunderflow(MIN,R):检测R是否出现下溢.

1. if Checkoverflow(MAX,R)=TRUE then

2.   return FPF;

3. else if Checkunderflow(MIN,R)=TRUE then

4.   retuen FPF;

5.  else

6.   return;

7.  end if

8. end if

2.6 异常返回

对于最终的异常返回,本文针对不同的异常类型预先设定了异常返回值,通过查表的形式确定返回值E.虽然查表法占用了一些存储空间,但却提高了异常处理的速度.总体而言,该方法牺牲空间,获得了时间.算法主要依据异常类型编码规则实现,通过对编码后各浮点位的判断确定异常返回值,其具体算法如下.

算法6. Exception:根据异常编码确定异常处理的操作及其返回值.

Inputs:exc_num,异常类型对应的编码;

R,核心运算结果;

fp_control:根据错误码设置浮点控制寄存器参数.

1. if exc_num=-1 then return;

2. t6 = exc_num & 0x40;

3. if t6!=0 then

4.   t8=(unsigned long)((exc_num^0x40)>>0x8) & 0x1;

5.   retv=retval_table[(4+((R>>0x3f) & 0x1)*4)+t8];

6. else

7.   t7=(unsigned long)(exc_num>>0x8) & 0x3f;

8.   retv=retval_table[t7];

9. end if

10. t14=exc_num & 0x3e;

11. if t14!=0 then

12.   fp_control();

13. end if

14. return retv;

3. 实验分析

本文将实现的异常处理方法应用于Mlib函数库[的浮点函数中(该数学库应用于2011年9月发布并安装在济南超算中心的神威蓝光超级计算机中).本实验在与神威蓝光同类型的某高性能计算机中的任意运算节点进行,该节点包括主核和从核两个运算核心,主核运行完整的操作系统,从核为64位RISC结构多用处理单元.其中,主核处理器主频为1 000MHz,内存主频400MHz,内存容量1.8GB;从核处理器主频为1200MHz,内存主频为800MHz,内存容量1.8GB.

Mlib函数库由基础函数库及SIMD扩展函数库,共计304个浮点函数组成.其中,SIMD扩展函数库由基础函数库通过SIMD指令扩展实现,与基础数学库具有相同的函数分类,包括三角函数、反三角函数、双曲函数、指数对数函数、伽马函数、取整取余函数、数值函数、误差函数、贝塞尔函数及其他函数等初等函数.

对应用本文方法前后的Mlib函数库进行了测试,测试结果表明:在应用本文方法前Mlib中有90.30%的函数会因为浮点异常而出现中断,而应用后这一比例被降到了0%.即:本文方法能够有效处理可能出现的浮点异常,且保证浮点函数不会因为浮点异常而出现中断.

在下面的测试中,本文对部分典型函数的测试结果进行了分析,包括sqrt,atan,pow,sin,fp_class和atan2函数,这些函数分别代表了不同的函数类型,且包含了各类的异常类型.

3.1 函数中的异常处理代码

对于异常处理最重要的衡量指标之一就是在其应用中所占的代码百分比.为了实现这一指标,本文对函数中计算代码和异常处理代码的条数进行了统计,结果如图4所示.

图4(Fig.4)

图4

典型函数中的异常处理代码比例

Fig.4

Exception handling code occupations among kernel functions

图4中的结果是部分典型函数的统计结果.一般程序中的异常处理代码是整个代码量的2/3左右[,但从测试结果看,却只有pow和atan2两个函数符合这个要求,fp_class函数的异常处理代码甚至为0%,浮点函数在数学上的一些特性决定了上述测试结果.如fp_class函数属于数值函数,其功能是检查输入参数属于哪类浮点数,这样的函数功能决定了该函数没有任何的计算,没有任何错误码,同样也不会有任何的异常处理代码; atan函数、sin函数在实现中需要处理的异常只有INV异常(由采用的算法决定),只需要很短的代码就能实现,所以其异常处理百分比都集中在10%左右,对于类似的三角函数(如cos,tan等)也具有同样的特点.

3.2 异常动作

区别于对异常代码量的统计,了解异常发生后带来的伴随动作的合理性,是衡量异常处理方法是否有效的又一重要指标.浮点函数在实现过程中,需要遵守函数本身的一些数学上的定义,发生异常该如何处理、返回值是什么,都可能和最初异常处理方法中设定的有出入.为了准确获取函数真实的异常动作,对代码量超过20万行运行于主从核的608个浮点函数进行了测试,虽然由于测试集数据量庞大的原因,并没有能够测到每个函数可能出现的所有异常处理,但依然反映出了一些性质,并将测试结果总结在表1中.

表1(Table 1)

表1 异常行为及其描述Table 1 Exception categories and their details

分类

描述

空

不出现异常,不作任何反应

标记

调用浮点控制寄存器,设置其值,主要用于INF异常

补指

当dnp参与运算且不被当作零处理时,通过强加一个大的指数,保证计算过程的可靠性

0

将dnp当作0处理

直接返回

将输入直接输出

继续

计算过程中出现异常,不作处理程序继续执行,一般在FPF异常中出现

返回

调用异常返回,返回预设的结果

表1 异常行为及其描述

Table 1 Exception categories and their details

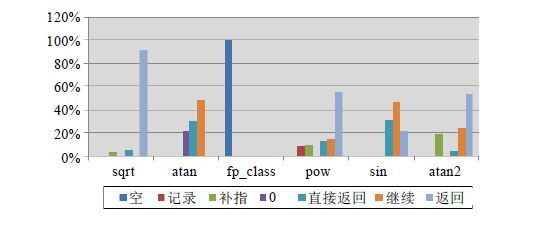
需要注意的是:对于一个在执行过程中的浮点函数可能出现多个异常行为,如某个函数在计算中将dnp当作0后继续计算,且在某处发生了溢出,在最后检测计算结果时调用了异常返回.这样的一个计算过程就触发了3种异常行为:0、继续和返回.因此,这样的一个异常处理过程将会被分别记录到这3种异常行为中.对于典型函数的统计结果,如图5所示.

图5(Fig.5)

图5

典型函数异常行为

Fig.5

Some kernel functions’ handling actions

空只在函数fp_class中出现,因为该函数不存在任何的异常,类似的数值类函数也都有同样的特点.对于sqrt函数,因为该函数主要处理的异常为参数小于0时的INV异常,其90%左右的异常行为都是返回.对于atan2函数,由于以x/y形式作为输入参数,与atan函数相比,就需要处理可能出现的下溢,表现的异常行为也有所不同,atan2函数明显需要更多的返回.从图5中可以看出:对于dnp的两种异常行为不会同时出现,在一个函数中要么将dnp当作0,要么进行补指,当然也可以直接返回.

3.3 异常触发的可能性

各种异常是否存在一定的关系?在浮点函数中,每一类异常触发的可能性又有多大?这是在本节测试中需要回答的问题.在测试中,将异常类型分为4大类9小类,大类分为DZE异常、INF异常、FPF异常和INV异常,小类按异常类型_返回值_错误码的形式分为INV_ZERO_EDOM,INV_NAN_EDOM,INV_INF_EDOM,UNF_ ZERO_ERANGE,OVF_NINF_ERANGE,OVF_INF_ERANGE,INF_NaN_ERANGE,DZE_NINF_EDOM和DZE_ INF_EDOM.

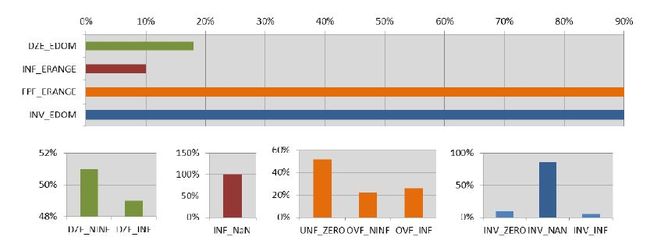
图6中的测试结果反映了各种异常行为被触发的可能性,例如:INF_ERANGE的10%表明,在Mlib中只有10%的函数可能发生INF异常;与之对应的INF_NaN的100%表明,触发INF异常后必然返回NaN.

从4个大类异常的角度对浮点函数进行测试统计后的结果如图6中的上半部分所示,最容易被触发的异常类型是FPF异常和INV异常,都达到了90%的可能.以INV_EDOM为例,返回值为NaN的异常类型触发的可能最大,达到了86%(INV_NaN).

图6(Fig.6)

图6

异常结果的可能性

Fig.6

Possibilities of exception results

3.4 异常对性能的干扰

虽然对于浮点函数有高可靠和高性能的要求,但高可靠往往比高性能更重要,只有保证函数高可靠的基础上,才能去不断实现对高性能的需求.判断异常处理方法是否有效,除了满足高可靠的要求,还需要满足对函数性能干扰尽量少的要求,干扰越少,说明方法越高效.本文通过对浮点函数使用异常处理方法前后的运行性能的对比测试,反映出异常处理方法的高效性.

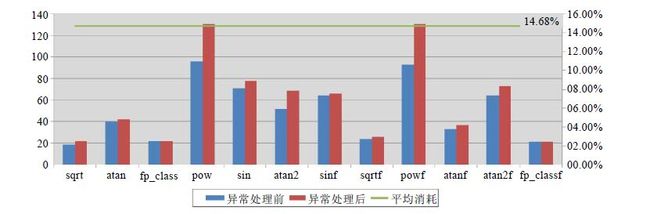
虽然浮点函数支持所有的浮点数,保证函数在执行过程中不会出现因浮点异常导致的程序中断,但是在正常的应用过程中,还是以正常区间的常用浮点数作为函数最频繁的输入.这些输入的运行路径都集中在函数的关键路径上,通过测试关键路径的运行性能,才能反映函数性能的真实运行情况.鉴于此,为了简化测试工作,保证每个函数都能尽可能地运行在关键路径,本文选取(0,1)之间的浮点数(对函数数学意义进行分析总结后确定的区间)对Mlib函数进行性能测试,通过对函数重复10万次的运行,计算函数的平均性能.测试结果如图7所示.

图7(Fig.7)

图7

异常处理前后的性能对比

Fig.7

Performance comparisons before and after exception handling

测试结果显示:经过异常处理后,函数的平均性能降低了14.68%((异常处理后-异常处理前)/异常处理前);同时,对于多数函数而言,异常处理也只带来了几拍到十几拍的性能消耗,完全在可接受的范围内.通过测试,进一步体现了本文方法的高效性.

4. 总 结

本文实现了一个分段式的异常处理方法,该方法面向汇编语言实现的浮点函数,并成功应用于Mlib函数库中.通过测试,该方法能够有效地提高浮点函数的可靠性,同时对浮点函数的性能干扰较少,能够满足浮点函数的高效性要求.相对于实验测试,理论验证总是显得更加可靠,虽然本文方法成功应用于浮点计算相对密集的浮点函数,并利用浮点计算应用最广泛的高性能计算平台进行测试,且在主从核共进行了600多个函数的测试,可依然无法百分之百地肯定本文方法完全正确.下一步,将尝试从理论验证的角度全面证明本文方法的可靠性,同时,将该异常处理方法扩展到更多的浮点计算型数值软件中.

致谢 在此,向评阅本文的审稿专家表示衷心的感谢,向对本文工作给予支持和建议的同行表示感谢.