chatgpt-4生成代码，看这一篇就够了

今天发现一个OpenAI的partnership基于gpt-4开发的好玩的code generation软件，分享一下

cursor

官网 https://www.cursor.so/
Build Software. Fast.
Write, edit, and chat about your code with GPT-4

直接下载安装就可以，使用起来也非常简单，ctrl+k 就可以输入命令生成代码。

示例

先看简介，可以生成，编辑，修改代码

// 1. Try generating with command K on a new line. Ask for a new react component of an error popup.
// 2. Then, select the outputted code and hit chat. Ask if there's a bug. Ask how to improve.
// 3. Try selecting some code and hitting edit. Ask the bot to add a button that updates a statefield.
// 4. To try out cursor on your own projects, go to file menu (top left) and open a folder.

python

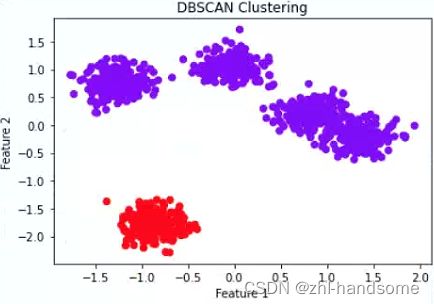
dbscan 聚类

prompt： Help me write a dbscan program

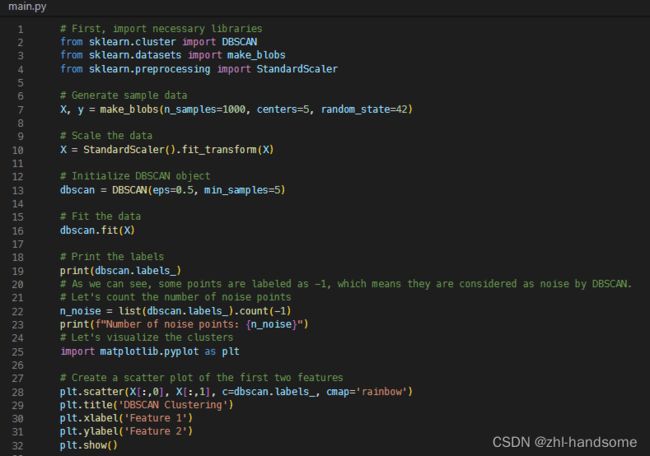
# First, import necessary libraries
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
# Generate sample data
X, y = make_blobs(n_samples=1000, centers=5, random_state=42)
# Scale the data
X = StandardScaler().fit_transform(X)
# Initialize DBSCAN object
dbscan = DBSCAN(eps=0.5, min_samples=5)
# Fit the data
dbscan.fit(X)
# Print the labels
print(dbscan.labels_)
# As we can see, some points are labeled as -1, which means they are considered as noise by DBSCAN.
# Let's count the number of noise points
n_noise = list(dbscan.labels_).count(-1)
print(f"Number of noise points: {n_noise}")
# Let's visualize the clusters
import matplotlib.pyplot as plt
# Create a scatter plot of the first two features
plt.scatter(X[:,0], X[:,1], c=dbscan.labels_, cmap='rainbow')
plt.title('DBSCAN Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

运行效果

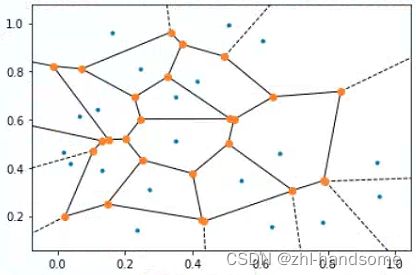
voronoi 图像分割

prompt： voronoi

import numpy as np
from scipy.spatial import Voronoi, voronoi_plot_2d
import matplotlib.pyplot as plt
# Generate sample data
points = np.random.rand(20, 2)
# Compute Voronoi tesselation
vor = Voronoi(points)
# Plot result
fig = voronoi_plot_2d(vor)
plt.show()

手写数字识别

Prompt: Write a handwritten digit recognition program

import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt

# Load the MNIST dataset
mnist = keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

# Normalize the images
train_images = train_images / 255.0
test_images = test_images / 255.0

# Define the model
model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(10)
])

# Compile the model
model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
              metrics=['accuracy'])

# Train the model
model.fit(train_images, train_labels, epochs=10)

# Evaluate the model
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
print('\nTest accuracy:', test_acc)

# Make predictions
probability_model = tf.keras.Sequential([model, tf.keras.layers.Softmax()])
predictions = probability_model.predict(test_images)

# Plot the first 25 test images and their predicted labels
plt.figure(figsize=(10,10))
for i in range(25):
    plt.subplot(5,5,i+1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(test_images[i], cmap=plt.cm.binary)
    predicted_label = np.argmax(predictions[i])
    true_label = test_labels[i]
    if predicted_label == true_label:
        color = 'white'
    else:
        color = 'red'
    plt.xlabel("{} ({})".format(predicted_label, true_label), color=color)
plt.show()

tf不太熟悉，简单解释下，先下载了mnist数据集，然后定义一个全连接网络，relu激活函数，adam优化器，训练十个epoch，看下结果

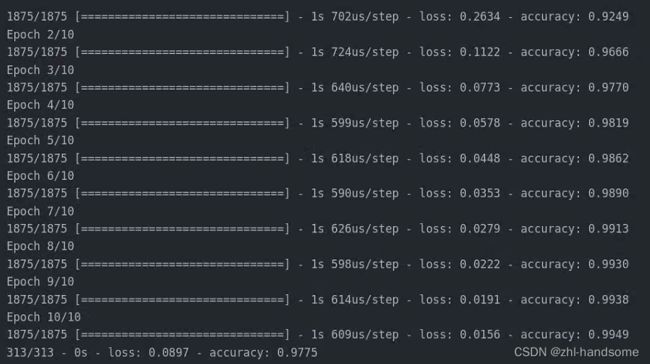
圆柱绕流

挺像回事的，可惜运行不出来，要我自己写也有难度

# Writing a program for the flow around a cylinder using the finite volume method# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt

# Define grid parameters
nx = 101  # Number of grid points in x-direction
ny = 101  # Number of grid points in y-direction
Lx = 4.0  # Length of domain in x-direction
Ly = 4.0  # Length of domain in y-direction
dx = Lx / (nx - 1)  # Grid spacing in x-direction
dy = Ly / (ny - 1)  # Grid spacing in y-direction
x = np.linspace(0.0, Lx, num=nx)  # Grid points in x-direction
y = np.linspace(0.0, Ly, num=ny)  # Grid points in y-direction
X, Y = np.meshgrid(x, y)  # Meshgrid of x and y points

# Define flow parameters
U_inf = 1.0  # Free-stream velocity
nu = 0.1  # Kinematic viscosity
Re = U_inf * Lx / nu  # Reynolds number
dt = 0.001  # Time step
nt = 1000  # Number of time steps

# Define initial conditions
u = np.zeros((ny, nx))  # x-velocity
v = np.zeros((ny, nx))  # y-velocity
p = np.zeros((ny, nx))  # Pressure
b = np.zeros((ny, nx))  # Source term

# Define functions for pressure Poisson equation
def laplacian(p, dx, dy):
    """
    Computes the Laplacian of a 2D scalar field.
    """
    pxx = (np.roll(p, -1, axis=1) - 2.0 * p + np.roll(p, 1, axis=1)) / dx ** 2
    pyy = (np.roll(p, -1, axis=0) - 2.0 * p + np.roll(p, 1, axis=0)) / dy ** 2
    return pxx + pyy

def poisson_p(p, b, dx, dy):
    """
    Solves the pressure Poisson equation using the Jacobi method.
    """
    pn = np.empty_like(p)
    pn[:] = p[:]
    for n in range(nt):
        pn[:] = p[:]
        p[1:-1, 1:-1] = (((pn[1:-1, 2:] + pn[1:-1, :-2]) * dy ** 2 +
                          (pn[2:, 1:-1] + pn[:-2, 1:-1]) * dx ** 2 -
                          b[1:-1, 1:-1] * dx ** 2 * dy ** 2) /
                         (2.0 * (dx ** 2 + dy ** 2)))
        p[:, -1] = p[:, -2]  # dp/dx = 0 at x = Lx
        p[0, :] = p[1, :]  # dp/dy = 0 at y = 0
        p[-1, :] = 0.0  # p = 0 at y = Ly
# Define source term
def build_up_b(b, rho, dt, u, v, dx, dy):
    """
    Builds the source term for the pressure Poisson equation.
    """
    b[1:-1, 1:-1] = (rho * (1.0 / dt *
                      ((u[1:-1, 2:] - u[1:-1, 0:-2]) / (2 * dx) +
                       (v[2:, 1:-1] - v[0:-2, 1:-1]) / (2 * dy)) -
                      ((u[1:-1, 2:] - u[1:-1, 0:-2]) / (2 * dx)) ** 2 -
                      2 * ((u[2:, 1:-1] - u[0:-2, 1:-1]) / (2 * dy) *
                           (v[1:-1, 2:] - v[1:-1, 0:-2]) / (2 * dx)) -
                      ((v[2:, 1:-1] - v[0:-2, 1:-1]) / (2 * dy)) ** 2))
    return b

# Define density
rho = 1.0
# Solve for velocity and pressure fields
for n in range(nt):
    un = u.copy()
    vn = v.copy()

    b = build_up_b(b, rho, dt, u, v, dx, dy)
    p = poisson_p(p, b, dx, dy)

    u[1:-1, 1:-1] = (un[1:-1, 1:-1] -
                     un[1:-1, 1:-1] * dt / dx *
                     (un[1:-1, 1:-1] - un[1:-1, 0:-2]) -
                     vn[1:-1, 1:-1] * dt / dy *
                     (un[1:-1, 1:-1] - un[0:-2, 1:-1]) -
                     dt / (2 * rho * dx) * (np.roll(p[1:-1, :], -1, axis=1) - np.roll(p[1:-1, :], 1, axis=1)) +
                     nu * (dt / dx ** 2 *
                           (un[1:-1, 2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) +
                           dt / dy ** 2 *
                           (un[2:, 1:-1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1])))

    v[1:-1, 1:-1] = (vn[1:-1, 1:-1] -
                     un[1:-1, 1:-1] * dt / dx *
                     (vn[1:-1, 1:-1] - vn[1:-1, 0:-2]) -
                     vn[1:-1, 1:-1] * dt / dy *
                     (vn[1:-1, 1:-1] - vn[0:-2, 1:-1]) -
                     dt / (2 * rho * dy) * (p[2:, 1:-1] - p[0:-2, 1:-1]) +
                     nu * (dt / dx ** 2 *
                           (vn[1:-1, 2:] - 2 * vn[1:-1, 1:-1] + vn[1:-1, 0:-2]) +
                           dt / dy ** 2 *
                           (vn[2:, 1:-1] - 2 * vn[1:-1, 1:-1] + vn[0:-2, 1:-1])))
# Plot velocity magnitude
vel_magnitude = np.sqrt(u ** 2 + v ** 2)
plt.figure(figsize=(6.0, 6.0))
plt.title('Velocity magnitude')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(0.0, Lx)
plt.ylim(0.0, Ly)
plt.contourf(X, Y, vel_magnitude, levels=np.linspace(0.0, 0.1, num=10))
plt.colorbar()
plt.show()

matlab

表白程序

Prompt ： Write a program to show love to a girl

disp('I love you more than words can express.');
disp('You are the most beautiful and amazing person I have ever met.');
disp('I promise to always be there for you, to support you, and to make you laugh.');
disp('I want to spend the rest of my life with you.');
disp('Will you be mine forever?');

常微分方程

Prompt ： Write a program for solving ordinary differential equations

% Define the differential equation
dydt = @(t,y) t*y^2;

% Define the initial condition
y0 = 1;

% Define the time interval
tspan = [0 1];

% Solve the differential equation
[t,y] = ode45(dydt,tspan,y0);

% Plot the solution
plot(t,y)
xlabel('Time')
ylabel('y')
title('Solution of dy/dt = ty^2')

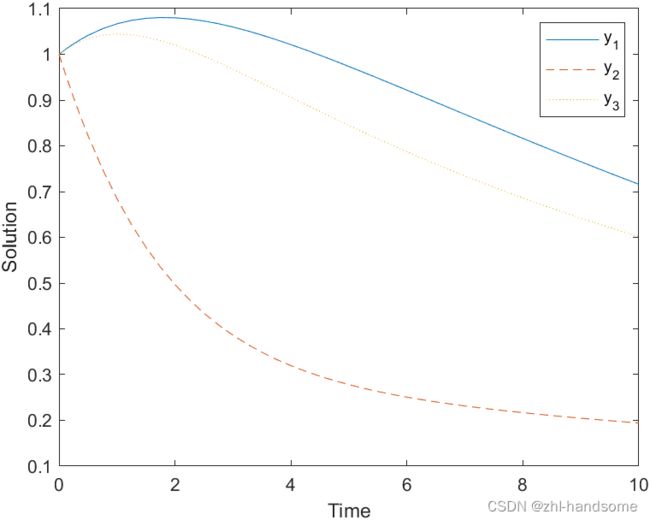
常微分方程组

Prompt ： Write a program for solving multiple ordinary differential equations
这个需要稍微修改一下顺序

% Define the initial conditions
y0 = [1; 1; 1];

% Define the time span
tspan = [0 10];

% Solve the system of differential equations
[t,y] = ode45(@myODEs, tspan, y0);

% Plot the results
plot(t,y(:,1),'-',t,y(:,2),'--',t,y(:,3),':');
legend('y_1','y_2','y_3');
xlabel('Time');
ylabel('Solution');


% Define the system of differential equations
function dydt = myODEs(t,y)
dydt = zeros(3,1);
dydt(1) = -0.1*y(1) + 0.2*y(2)*y(3);
dydt(2) = 0.1*y(1) - 0.2*y(2)*y(3) - 0.3*y(2);
dydt(3) = 0.2*y(1) + 0.3*y(2) - 0.4*y(3);

end

运行结果:

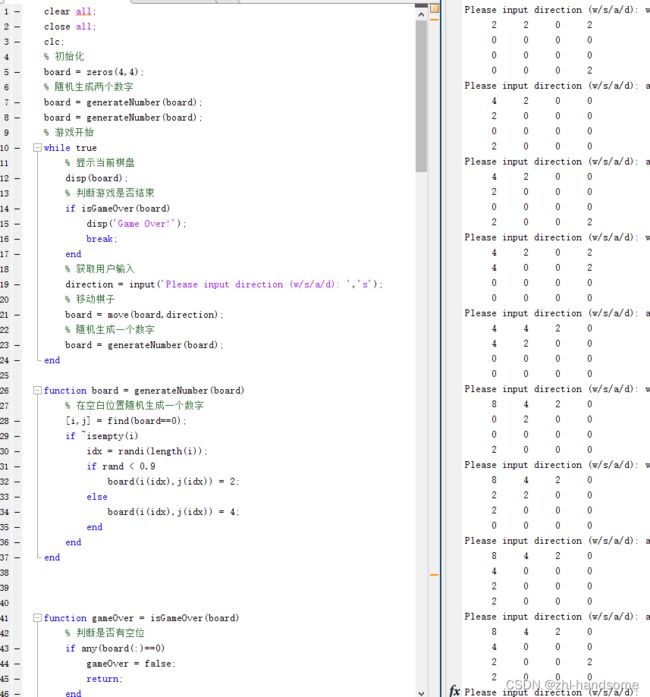
2048小游戏

clear all;
close all;
clc;
% 初始化
board = zeros(4,4);
% 随机生成两个数字
board = generateNumber(board);
board = generateNumber(board);
% 游戏开始
while true
    % 显示当前棋盘
    disp(board);
    % 判断游戏是否结束
    if isGameOver(board)
        disp('Game Over!');
        break;
    end
    % 获取用户输入
    direction = input('Please input direction (w/s/a/d): ','s');
    % 移动棋子
    board = move(board,direction);
    % 随机生成一个数字
    board = generateNumber(board);
end

function board = generateNumber(board)
    % 在空白位置随机生成一个数字
    [i,j] = find(board==0);
    if ~isempty(i)
        idx = randi(length(i));
        if rand < 0.9
            board(i(idx),j(idx)) = 2;
        else
            board(i(idx),j(idx)) = 4;
        end
    end
end



function gameOver = isGameOver(board)
    % 判断是否有空位
    if any(board(:)==0)
        gameOver = false;
        return;
    end
    % 判断是否有相邻的相同数字
    [m,n] = size(board);
    for i = 1:m
        for j = 1:n-1
            if board(i,j)==board(i,j+1)
                gameOver = false;
                return;
            end
        end
    end
    for i = 1:m-1
        for j = 1:n
            if board(i,j)==board(i+1,j)
                gameOver = false;
                return;
            end
        end
    end
    % 没有空位，也没有相邻的相同数字，游戏结束
    gameOver = true;
end

function board = move(board,direction)
    % 根据方向移动棋子
    switch direction
        case 'w'
            for j = 1:4
                % 向上合并
                for i = 1:3
                    if board(i,j)==0
                        continue;
                    end
                    for k = i+1:4
                        if board(k,j)==0
                            continue;
                        elseif board(k,j)==board(i,j)
                            board(i,j) = board(i,j)*2;
                            board(k,j) = 0;
                            break;
                        else
                            break;
                        end
                    end
                end
                % 向上移动
                for i = 1:3
                    if board(i,j)==0
                        for k = i+1:4
                            if board(k,j)~=0
                                board(i,j) = board(k,j);
                                board(k,j) = 0;
                                break;
                            end
                        end
                    end
                end
            end
        case 's'
            for j = 1:4
                % 向下合并
                for i = 4:-1:2
                    if board(i,j)==0
                        continue;
                    end
                    for k = i-1:-1:1
                        if board(k,j)==0
                            continue;
                        elseif board(k,j)==board(i,j)
                            board(i,j) = board(i,j)*2;
                            board(k,j) = 0;
                            break;
                        else
                            break;
                        end
                    end
                end
                % 向下移动
                for i = 4:-1:2
                    if board(i,j)==0
                        for k = i-1:-1:1
                            if board(k,j)~=0
                                board(i,j) = board(k,j);
                                board(k,j) = 0;
                                break;
                            end
                        end
                    end
                end
            end
        case 'a'
            for i = 1:4
                % 向左合并
                for j = 1:3
                    if board(i,j)==0
                        continue;
                    end
                    for k = j+1:4
                        if board(i,k)==0
                            continue;
                        elseif board(i,k)==board(i,j)
                            board(i,j) = board(i,j)*2;
                            board(i,k) = 0;
                            break;
                        else
                            break;
                        end
                    end
                end
                % 向左移动
                for j = 1:3
                    if board(i,j)==0
                        for k = j+1:4
                            if board(i,k)~=0
                                board(i,j) = board(i,k);
                                board(i,k) = 0;
                                continue;
                            end
                        end
                    end
                end
            end
        case 'd'
            for i = 1:4
                % 向右合并
                for j = 4:-1:2
                    if board(i,j)==0
                        continue;
                    end
                    for k = j-1:-1:1
                        if board(i,k)==0
                            continue;
                        elseif board(i,k)==board(i,j)
                            board(i,j) = board(i,j)*2;
                            board(i,k) = 0;
                            break;
                        else
                            break;
                        end
                    end
                end
                % 向右移动
                for j = 4:-1:2
                    if board(i,j)==0
                        for k = j-1:-1:1
                            if board(i,k)~=0
                                board(i,j) = board(i,k);
                                board(i,k) = 0;
                                continue;
                            end
                        end
                    end
                end
            end
    end
end

运行效果

C/C++

来刷会leecode吧，直接上困难强度

正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。


示例 1：
输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例 2:
输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：
输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/regular-expression-matching
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

没给头文件，还得我自己加。。。

#include 
#include 
#include 
using namespace std;

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size(), n = p.size();
        vector<vector<bool>> dp(m + 1, vector<bool>(n + 1, false));
        dp[0][0] = true;
        for (int i = 0; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (p[j - 1] == '*') {
                    dp[i][j] = dp[i][j - 2];
                    if (matches(s, p, i, j - 1)) {
                        dp[i][j] = dp[i][j] || dp[i - 1][j];
                    }
                }
                else {
                    if (matches(s, p, i, j)) {
                        dp[i][j] = dp[i - 1][j - 1];
                    }
                }
            }
        }
        return dp[m][n];
    }

    bool matches(string& s, string& p, int i, int j) {
        if (i == 0) {
            return false;
        }
        if (p[j - 1] == '.') {
            return true;
        }
        return s[i - 1] == p[j - 1];
    }
};
int main() {
    Solution s;
    string str = "ab";
    string pattern = ".*";
    cout << s.isMatch(str, pattern) << endl;
    return 0;
}

有兴趣自己拿去测试，写的是对的

删除有序数组中的重复项

太简单了我都会

删除有序数组中的重复项
给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/remove-duplicates-from-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

#include 
#include 
#include 
using namespace std;


int removeDuplicates(vector<int>& nums) {
    if (nums.empty()) {
        return 0;
    }
    int i = 0;
    for (int j = 1; j < nums.size(); j++) {
        if (nums[j] != nums[i]) {
            i++;
            nums[i] = nums[j];
        }
    }
    return i + 1;
}
int main() {
    vector<int> nums = { 9,9 ,1, 1, 2, 2, 2, 3, 4, 5, 5 };
    int len = removeDuplicates(nums);
    for (int i = 0; i < len; i++) {
        cout << nums[i] << " ";
    }
    cout << endl;
    return 0;
}
// Output: 1 2 3 4 5

n 皇后问题

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/n-queens
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

#include 
#include 
#include 
using namespace std;


class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> res;
        vector<string> board(n, string(n, '.'));
        backtrack(res, board, 0);
        return res;
    }

    void backtrack(vector<vector<string>>& res, vector<string>& board, int row) {
        if (row == board.size()) {
            res.push_back(board);
            return;
        }

        for (int col = 0; col < board.size(); col++) {
            if (!isValid(board, row, col)) continue;
            board[row][col] = 'Q';
            backtrack(res, board, row + 1);
            board[row][col] = '.';
        }
    }

    bool isValid(vector<string>& board, int row, int col) {
        for (int i = 0; i < row; i++) {
            if (board[i][col] == 'Q') return false;
        }
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (board[i][j] == 'Q') return false;
        }
        for (int i = row - 1, j = col + 1; i >= 0 && j < board.size(); i--, j++) {
            if (board[i][j] == 'Q') return false;
        }
        return true;
    }
};
int main() {
    Solution s;
    vector<vector<string>> res = s.solveNQueens(5);
    for (auto& board : res) {
        for (auto& row : board) {
            cout << row << endl;
        }
        cout << endl;
    }
    return 0;
}
/*
output:
...Q.
Q....
..Q..
....Q
.Q...

...Q.
.Q...
....Q
..Q..
Q....

....Q
.Q...
...Q.
Q....
..Q..

....Q
..Q..
Q....
...Q.
.Q...
*/

我怀疑这是个搜索引擎。。。

总结

体验下来能写一些基础的程序，支持 html / css / python / c / rust / go / c# / java / php / matlab等语言，用来写点小工具还是非常不错的，可以说比我水平高多了，gpt4果然有点东西。
估计未来可重复性的程序员的工作会被替代，可以说大大降低了编程的门槛，但同时生成的代码也需要有一定基础的人去修改，对于我们搞cfd的影响还不大，用来做做数据处理挺好。
最后，一定要做一个会提问的人！