动态因果图模型

阅前须知：本文为对《复杂系统因果图推理理论与算法研究》的阅读笔记

1. 动态因果图模型

1.1 引言

动态因果图知识表达模型，简称因果图，是一种以概率论为理论基础的知识表达推理模型，与信度网(Belief Network)一样，属于基于不确定性的推理算法研究领域。不确定性知识表达和推理通常可分为两类：

• 基于概率的方法，如信度网、马尔可夫网等
• 非概率的方法，包括MHYCIN的确定性因子、模糊逻辑等

1.1.1 信度网的应用与不足

目前国外的许多研究机构都对信度网进行了深入的研究，许多领域也引入了该理论，例如工业上的故障诊断(如美国通用电气公司的Auxiliary Turbine Diagnosis)、 航天故障诊断(如美国航空航天局和Rockwell公司联合研制的Diagnosis of space shuttle propulsion systems)、 军事目标自动识别、作战意图自动估计、无人自动驾驶、医学上的病理诊断、商业上的金融市场分析、信息智能检索、基于概率因果关系的数据挖掘、软件产业上的智能帮助系统等。
然而，信度网也存在一些不足：

• 处理多连通问题和因果循环问题的方法复杂，计算量大
• 采用条件概率表达因果关系强度不直观，数据之间存在相依性
• 较难根据实时收到的信息对知识库中的数据和因果结构进行在线修改
• 没有考虑条件概率随时间动态变化等问题

随着对信度网研究的不断深入，一些包含信度网知识表达方式精华、针对某些特定领域进行优化了的基于概率论的推理模型也被相继提出，动态因果图推理模型就是其中之一。

1.1.2 因果图的优势

因果图通过引入布尔逻辑运算，克服了上述信度网之不足，具有如下一些显著的特点:

• 完全基于概率论，有良好的理论基础
• 对网络的拓扑结构没有限制(不要求通常使用的DAG图)，可根据实际情况任意构造自己的网络
• 在网络中引入了逻辑门，使得对因果关系的表达更加清晰、自然、容易理解、便于解释
• 采用直接因果强度而不是条件概率，避免了在给定知识时知识间的相关性问题,符合客观实际，更便于知识表达
• 具有灵活的推理方式，既能由因到果，也可由果到因，还可因果混合推理
• 在结构中引入了动态特性，能根据在线情况的变化动态变换网络结构，使之更符合当前时刻的客观实际

1.2 模型主要思想

因果图采用图形表示因果关系，节点表示事件或变量，有向边表示因果关系，并用连接强度来表示因果关系的强度。因果图是从信度网基础上发展起来的，一个允许具有环路的有向图。

1.3 模型的表达方式

圆圈节点:表示一个中间事件，或者中间变量。中间事件是至少含有一-条输入边，可以不含或含有一至多条输出边的事件。

方框节点:表示一个基本事件，或者基本变量。基本事件是不含有任何输入边但至少含有一条输出边的事件。为方便表达，中间事件和基本事件统称为节点事件。

门节点:表示一个逻辑门(与门、或门等等)，它把输入变量通过逻辑运算组合成输出变量。逻辑门要求至少含有两条输入边和一条及以上输出边。

连接边:表示一个连接事件，或者连接变量。连接事件可以从基本事件、中间事件和逻辑门出发，始终指向中间事件。指向同一个中间事件的所有连接事件是“或”关系。它表示当该连接边的父节点发生的情况下是否会导致子节点发生，即子节点事件发生的条件是父节点事件发生并且该连接事件发生。从数值上其概率表示父节点与子节点间的因果强度，但作为一个事件，它与父节点事件相互独立。可见连接事件之间相互独立，而且连接事件与基本事件之间也相互独立。

1.3.1 因果图与故障诊断

在因果图知识表达中，基本事件没有输入边，可以看成是导致中间事件发生变化的原因，在针对于故障诊断领域时，通常可以将基本事件看成是故障；而中间事件至少含有一条输入边，可以不含或含有一至多条输出边，在针对于故障诊断领域时，通常将中间事件看成是可以通过物理手段(比如温度传感器)得到的参数或者某种现象(比如某指示灯亮了)，在构造因果图模型时，由专家构造故障同现象之间的因果关系；在推理时，则根据现象和参数确定故障(基本事件)发生的概率。

1.3.2 因果图分类

因果图可以是基于事件的，即图中每个图形符号表示一个事件;也可以是基于变量的，即图中每个图形符号表示一个变量。基于事件的因果图我们称为单值因果图，基于离散变量的因果图我们称为多值因果图，单值因果图和多值因果图称为离散因果图。如果因果图中的变量为连续变量，我们称之为连续因果图，还可以是离散和连续混合的因果图。

1.3.3 因果图形式化表示

因果图知识表达方式可以形式化表示为: $C=<S，A，R>$，且$S=<X，B，G，P>$

其中符号含义如下: $C$-因果图模型; $S$-因果图结构，是一个可以含有向环的有向图，它由基本事件、中间事件、逻辑门、连接事件组成; $X$一中间事件，$B$-基本事件；$G$-逻辑门，$P$-连接事件；$A$-参数，包括基本事件的先验概率、连接事件的连接强度、连接事件连接的父节点与子节点之间的相关系数等; $R$-基于$S$和$A$的推理机。

1.3.4 因果图的正规化

最多只含有逻辑与门(AND)和逻辑或门(OR)的因果图称为正规化的因果图。通过逻辑门的等效变换，去除因果图中的非逻辑与门和非逻辑或门，称为因果图的正规化。

1.4 因果树

1.4.1 微因果树

因果图中的每个节点事件(或变量)对应一棵微因果树,微因果树的树根就是对应的节点事件(或变量)。微因果树中的菱形为与树根节点相邻的节点事件(或变量);圆圈为与树根节点相邻的基本事件( 或变量);有标注的线为连接事件(或变量)，它使输入事件(或变量)通过逻辑门引起输出的顶事件(或变量);矩形描述了事件(或变量)与逻辑门的内容。

1.4.2 因果树与因果图对比

在表达一些大的复杂的知识时，由于微因果树将全局知识分解成一些小模块，通常它比因果图具有更大的灵活性；另一方面， 它不能象因果图那样对领域知识提供一个全局、直观的表达。因此，当领域知识的规模较小时，使用因果图来表达比较合适一些；当领域知识的规模较大时，使用因果树来表达更好一些。

2.动态因果图推理

因果图推理中有三种重要推理模式：

• 因果推理或正向推理$P(X|Causes)$
• 诊断推理或反向推理$P(X|Evidences)$
• 辩解或因果混合推理$P(X|Causes$ & $Evidences)$

2.1 待求解问题的数学形式

在给定因果图$C$的结构及参数情况下求解$P(H|E)$，其中E为C中所观察到的证据集合，$E=E$₁$\cap \dots \cap E$_k, $H$为$C$中待考察的事件。

采用贝叶斯公式，$P(H|E)$可表示为：
$$P(H|E)=\frac{P(H,E)}{P(E)}=\frac{P(H\cap E)}{P(E)}=\frac{P(H\cap E_1\cap \dots \cap E_k)}{P(E_1\cap \dots \cap E_k)}$$

其中$H、E_1、\dots E_k$均为节点事件。在因果图中假定基本事件和连接事件的概率值已知且独立。在进行推理时首先要将上式中的各项表达为基本事件和连接事件的逻辑表达式，然后再计算其概率值。为了简化推理运算，在推理之前需要对因果图进行编译，以得到所有中间事件的逻辑表达式。在逻辑表达式的右边均为基本事件和连接事件。

2.2 割集

割集(cut set, CS)就是一组事件(包括基本事件、节点事件、逻辑门事件、连接事件)以逻辑与的关系组合在一起，表示某几个事件同时发生将引起中间事件的发生。每个割集(CS) 之间的关系为逻辑或。

2.2.1 一阶割集

仅由和某节点事件相邻的事件构成的割集称为一阶割集。

2.2.2 最终割集

仅用基本事件和连接事件表示的割集表达式称为节点事件的最终割集。
对于中间事件的任一最终割集， 如果去掉其中任意一个基本事件后，就不再是割集。因此这个最终割集称为这个中间事件的故障模式。

2.3 因果图编译

2.3.1 逻辑解环

主要目的：消除因果图中存在的有向环路，该过程针对每一个中间事件节点单独进行。

解环规则：一个节点不能在同一时刻成为自己的原因。

主要思想：针对每一个节点求解以该节点为根的一棵树，要求该树的每一条支路上不存在相同的节点，且如果对该树的任一节点继续展开将会破坏上述要求。

2.3.2 求最终割集式

对因果树中的每一个节点，根据前面因果图的定义该节点可以表达成它子节点的逻辑“或”。假设一个节点有m条入边，则该节点可以展开为至少m个割集。下列公式是图2.3中每一棵树根节点的逻辑展开式。

$$\begin{array}{rl}& X_1=B_6\cup P_{31}{X}_3\\ & X_2=B_7\cup P_{12}{X}_1\\ & X_3=P_{83}{B}_8\cup P_{53}{G}_5\cup P_{43}{X}_4\\ & X_4=P_{24}{X}_2\cup B_9\cup P_{54}{G}_5\cup P_{74}{B}_7\cup P_{34}{X}_3\end{array}$$
上述公式中，右边每一项都是一个割集CS。由于只涉及与节点相邻的连接事件和节点事件，上述割集表达式称为一阶割集表达式，简称CS_s-1。而我们想要的是将中间事件表达为仅含基本事件和连接事件的逻辑公式，因此需要进一步展开，消去CS_s-1中所有的中间事件，得到的最终割集表达式，简称为CS_s-f。

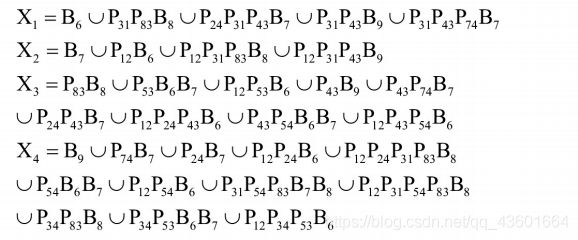
虽然上述公式右侧每一个时间的概率均已知且独立，但是由于其中可能存在的相交关系，我们并不能简单的对右侧割集的概率进行求和，因此，我们需要对CS_s-f进行不交化处理以便可以对其直接求和计算。

2.3.3 求不交化割集

即让各个割集之间互斥，使其并集的概率可以简单化为各个割集概率的和。

$$X=c{s}_1+c{s}_2\overline{c{s}_1}+c{s}_3\overline{c{s}_1}\overline{c{s}_2}+\dots +c{s}_m\overline{c{s}_1}\overline{c{s}_2}\dots \overline{c{s}_{m-1}}$$
其中$c{s}_i$为原割集。

2.4 因果图计算简化

2.4.1 定理1

设$$\begin{gathered} A=X_1\cup X_2\cup \dots \cup X_m,B=Y_1\cup Y_2\cup \dots \cup Y_n,X_1,X_2,\dots ,X_m,Y_1,Y_2, \\ \dots ,Y_n \end{gathered}$$是不同的基本事件，且相互独立，那么$A,B$相互独立。

2.4.2 定理2

设$$\begin{gathered} T=A\cap B,A=X_1\cup X_2\cup \dots \cup X_m,B=Y_1\cup Y_2\cup \dots \cup Y_n,X_1,X_2,\dots , \\ {X}_m,Y_1,Y_2,\dots ,Y_n \end{gathered}$$是不同的基本事件，且相互独立，则有$T$的不交化割集为
$$T=(X_1+X_2\overline{X_1}+\dots +X_m\overline{X_{m-1}}\dots \overline{X_2}\overline{X_1})(Y_1+Y_2\overline{Y_1}+\dots +Y_n\overline{Y_{n-1}}\dots \overline{Y_2}\overline{Y_1})$$

2.4.3 定理3

不交化割集的交也是不交化割集。

2.4.4

由上述三个定理可知，如果两事件$A$与$B$相互独立，求$AB$的不交化割集可以通过分别求$A$与$B$的不交化割集来完成，从而简化了因果图中不交化割集的计算。

3.动态因果图研究方向

• 带有有向环的复杂系统的推理算法
• 研究多值离散因果图问题
• 研究连续因果图问题
• 研究离散、连续混合的因果图计算问题
• 研究因果图的动态问题
• 研究连续过程系统中的初因和非初因事件的不同含义和多重事件推理问题
• 研究虚假信号和不完美知识库的问题
• 研究因果图与信度网之间的转换问题
• 研究高效的精确算法与近似算法
• 研究开发对应于上述各种问题解决方案的计算机软件