计算机视觉：基本图像操作和处理

一、直方图

1.基本原理

直方图(histogram)是从总体中随机抽取样本，将样本数据加以整理，用于了解数据的分布情况，使我们比较容易直接看到数据的位置状况、离散程度和分布形状的一种常用工具。它是一系列宽度相等、高度不等的长方形来表示数据，其宽度代表组距，高度代表指定组距内的数据数(频数)。

直方图的作用：

• 直观地显示质量特性的分布状态，对于数据的分布形状、中心位置和分散程度一目了然；
• 关注数据和规格的关系，通过测定值与规格值比较，判断出不良是平均不良还是异常不良，便于人们确定在何处进行质量改进。(平均不良代表系统问题，是整个过程的不良；异常不良代表个别离散不良，属于个别问题)
• 比较改善前后的直方图，可了解平均值、分散、分布形状的变化，改善的效果如何。

2.实例

(1)原图
(2)灰度图

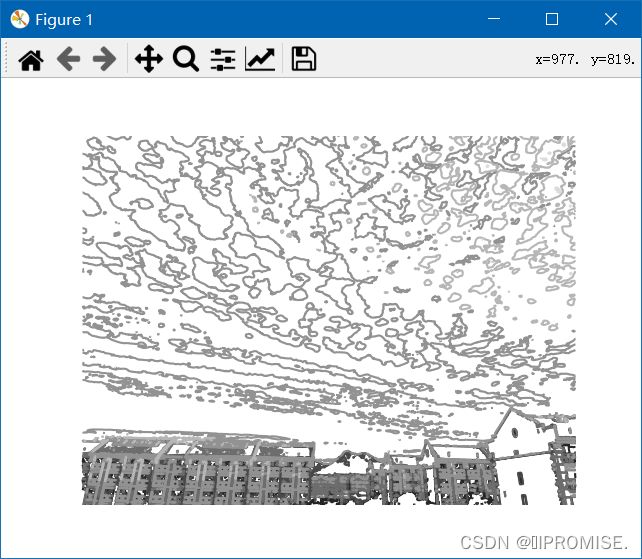
(3)直方图

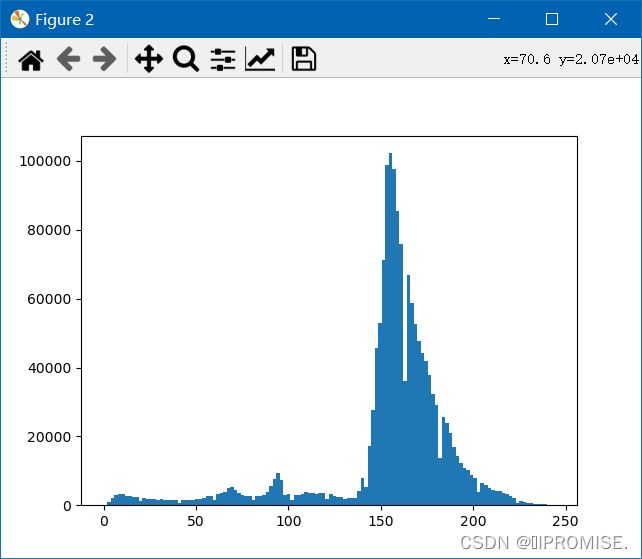
(4)python源码

#读取图像到数组中
im = array(Image.open('images/vision01.jpg').convert('L'))
#新建一个图像
figure()
#不使用颜色信息
gray()
#在原点左上角显示轮廓图像
contour(im, origin='image')
axis('equal')
axis('off')
figure()
hist(im.flatten(), 128)
show()

二、直方图均衡化

1.基本原理

直方图均衡化是指将一幅图像的灰度直方图变平，使变换后的图像中每个灰度值的分布概率都相同。在对图像做进一步处理之前，直方图均衡化通常是对图像灰度值进行归一化的一个非常好的方法，并且可以增强图像的对比度。
直方图均衡化(Histogram Equalization)是一种增强图像对比度(Image Contrast)的方法，其主要思想是将一副图像的直方图分布变成近似均匀分布，从而增强图像的对比度。

原理分析：假设我们现在有一个图像A，其直方图分布 HA(D) ，我们想利用一个单调非线性映射f : R --> R，将图像A变为图像B，即对图像A中每个 像素点施加f变换 ，图像B的直方图分布为HB(D)。整个过程可以按照以下图示来说明：图中右下方是A图像的灰度直方图分布，图中右上方是单调非线性变换函数f ，左上方式得到的图像B的直方图分布，其中有DB = f(DA)， DB + ΔDB = f(DA + ΔDA)。即可以理解f的作用是将A图像里面像素点灰度为DA的全部变为DB，那么则有：

上面公式可以理解为对应区间内像素点总数不变。为了实现直方图均衡化，特殊地有：

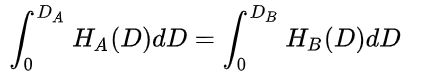
因为目标是直方图均匀分布，那么理想的
，A0是 像素点个数， L是灰度级深度，通常取256。那么得到：

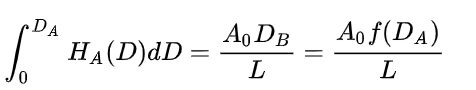
那么 ，f就可以求出来了，结果为：

离散形式为：


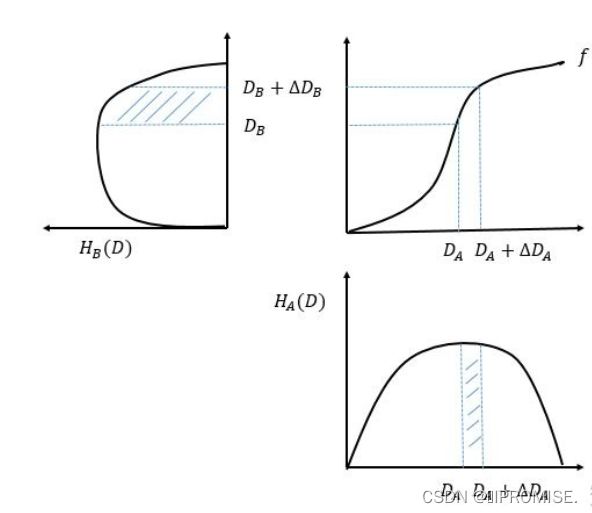
图示：直方图均衡化示意图
通过上面推导过程可以看出，映射函数 [公式] 和CDF密切相关。并且，推导过程是在连续分布上作的处理，而实际上图像灰度级别通常是256，故是一种以离散情况近似了连续分布，如果灰度级别足够高的话产生的结果会是真正均匀分布的直方图，由于灰度级只有256，故而实际情况中得到的直方图往往不是均匀分布，而是近似均匀分布的。同时，假若A图像的灰度直方图变化剧烈，且某些灰度区间不存在像素点，这会造成CDF的剧烈变化，那么在灰度区间(x, x+1)内即可能发生剧烈的变化，从而导致最后产生的B图像的直方图也有较大的不均匀性。但是，实际使用过程中，得到的图像能近似均匀分布已经能达到比较好的对比度增强效果了。

2.实例

(1)原图

(2)直方图均衡化前后

(3)均衡化前后


(4)python源码

# 计算累计分布函数
def C(rk):
  # 读取图片灰度直方图
  # bins为直方图直方柱的取值向量
  # hist为bins各取值区间上的频数取值
  hist, bins = np.histogram(rk, 256, [0, 256])
  # 计算累计分布函数
  return hist.cumsum()

# 计算灰度均衡化映射
def T(rk):
  cdf = C(rk)
  # 均衡化
  cdf = (cdf - cdf.min()) * (255 - 0) / (cdf.max() - cdf.min()) + 0
  return cdf.astype('uint8')


def histeq():
    # 读取图片
    img = cv.imread('./images/vision01.jpg', 0)
    # 将二维数字图像矩阵转变为一维向量
    rk = img.flatten()

    # 原始图像灰度直方图
    plt.hist(rk, 256, [0, 255], color='r')
    cv.imshow("Before histeq", img)

    # 直方图均衡化
    imgDst = T(rk)[img]
    cv.imshow("After histeq", imgDst)
    plt.hist(imgDst.flatten(), 256, [0, 255], color='b')

    plt.show()

三、高斯滤波

1.基本原理

高斯滤波是一种线性滤波器，能够有效抑制噪声，平滑图像。其作用原理和均值滤波器类似，都是取滤波器窗口内的像素的均值作为输出。其窗口模板的系数和均值滤波器不同，均值滤波器的模板系数相同且都为1；而高斯滤波器的模板系数则随着距离模板中心的增大而系数减小。所以高斯滤波器相比于均值滤波器对图像的模糊程度较小。
图像大多数噪声均属于高斯噪声，因此高斯滤波器应用也较广泛。高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像去噪。
可以简单地理解为，高斯滤波去噪就是对整幅图像像素值进行加权平均，针对每一个像素点的值，都由其本身值和邻域内的其他像素值经过加权平均后得到。
高斯滤波的具体操作是：用一个用户指定的模板（或称卷积、掩膜）去扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

高斯函数：

注：σ的大小决定了高斯函数的宽度。

高斯核
理论上，高斯分布在所有定义域上都有非负值，这就需要一个无限大的卷积核。实际上，仅需要取均值周围3倍标准差内的值，以外部份直接去掉即可。
高斯滤波的重要两步就是先找到高斯模板然后再进行卷积，模板。
举个栗子：
假定中心点的坐标是（0,0），那么取距离它最近的8个点坐标，为了计算，需要设定σ的值。假定σ=1.5，则模糊半径为1的高斯模板就算如下：

这个时候我们我们还要确保这九个点加起来为1（这个是高斯模板的特性），这9个点的权重总和等于0.4787147，因此上面9个值还要分别除以0.4787147，得到最终的高斯模板。

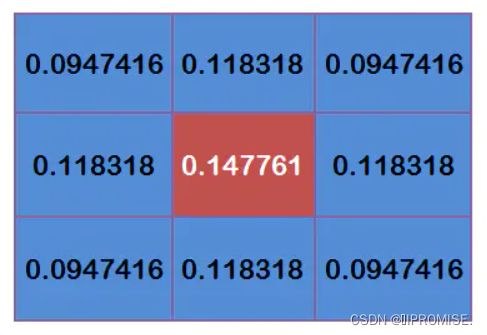
高斯滤波计算
假设现有9个像素点，灰度值（0-255）的高斯滤波计算如下：

将这9个值加起来，就是中心点的高斯滤波的值。
对所有点重复这个过程，就得到了高斯模糊后的图像。

高斯滤波步骤
（1）移动相关核的中心元素，使它位于输入图像待处理像素的正上方
（2）将输入图像的像素值作为权重，乘以相关核
（3）将上面各步得到的结果相加做为输出
简单来说就是根据高斯分布得到高斯模板然后做卷积相加的一个过程。

2.实例

(1)原图

(2)σ=2的高斯滤波图像

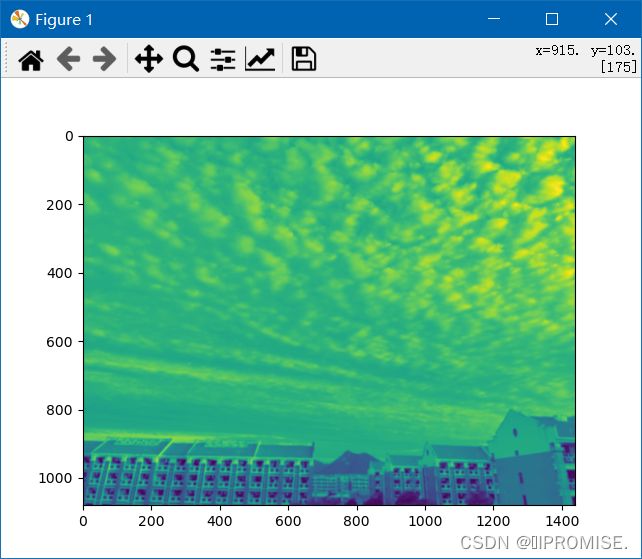
(3)σ=5的高斯滤波图像

(4)σ=10的高斯滤波图像

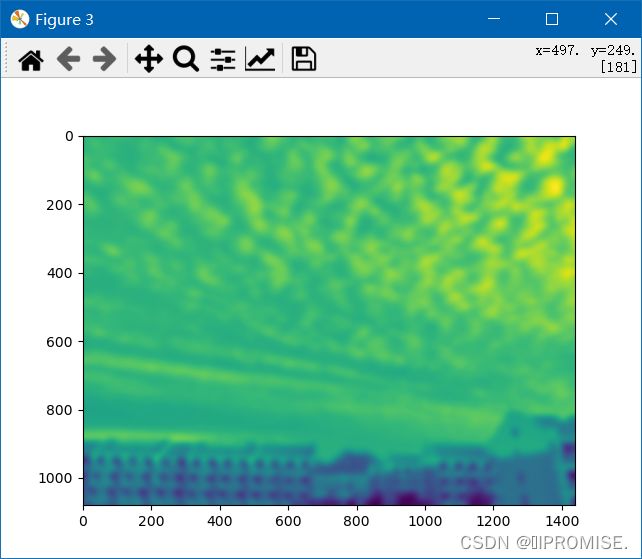
(5)python源码

im = array(Image.open('./images/vision01.jpg').convert('L'))
im2 = filters.gaussian_filter(im, 2)
im3 = filters.gaussian_filter(im, 5)
im4 = filters.gaussian_filter(im, 10)
figure()
imshow(im2)
figure()
imshow(im3)
figure()
imshow(im4)
show()