ResNet详解与分析

博客： 博客园 | CSDN | blog

Resnet要解决的是什么问题

ResNets要解决的是深度神经网络的“退化”问题。

什么是“退化”？

我们知道，对浅层网络逐渐叠加layers，模型在训练集和测试集上的性能会变好，因为模型复杂度更高了，表达能力更强了，可以对潜在的映射关系拟合得更好。 而** “退化”指的是，给网络叠加更多的层后，性能却快速下降的情况。 **

训练集上的性能下降，可以排除过拟合，BN层的引入也基本解决了plain net的梯度消失和梯度爆炸问题。 如果不是过拟合以及梯度消失导致的，那原因是什么？

按道理，给网络叠加更多层，浅层网络的解空间是包含在深层网络的解空间中的，深层网络的解空间至少存在不差于浅层网络的解，因为只需将增加的层变成恒等映射，其他层的权重原封不动copy浅层网络，就可以获得与浅层网络同样的性能。更好的解明明存在，为什么找不到？找到的反而是更差的解？

显然，这是个优化问题，反映出结构相似的模型，其优化难度是不一样的，且难度的增长并不是线性的，越深的模型越难以优化。

有两种解决思路，一种是调整求解方法，比如更好的初始化、更好的梯度下降算法等；另一种是调整模型结构，让模型更易于优化——改变模型结构实际上是改变了error surface的形态。

ResNet的作者从后者入手，探求更好的模型结构。将堆叠的几层layer称之为一个block，对于某个block，其可以拟合的函数为$F(x)$，如果期望的潜在映射为$H(x)$，**与其让$F(x)$ 直接学习潜在的映射，不如去学习残差$H(x)-x$，即$F(x):=H(x)-x$，这样原本的前向路径上就变成了$F(x)+x$，用$F(x)+x$来拟合$H(x)$。作者认为这样可能更易于优化，因为相比于让$F(x)$学习成恒等映射，让$F(x)$学习成0要更加容易——后者通过L2正则就可以轻松实现。**这样，对于冗余的block，只需$F(x)\to 0$就可以得到恒等映射，性能不减。

Instead of hoping each few stacked layers directly fit a desired underlying mapping, we explicitly let these layers fit a residual mapping. Formally, denoting the desired underlying mapping as $H(x)$, we let the stacked nonlinear layers fit another mapping of $F(x):=H(x)-x$. The original mapping is recast into $F(x)+x$. We hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.

—— from Deep Residual Learning for Image Recognition

下面的问题就变成了$F(x)+x$ 该怎么设计了。

Residual Block的设计

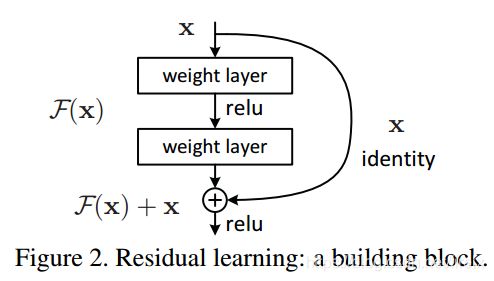
$F(x)+x$构成的block称之为Residual Block，即残差块，如下图所示，多个相似的Residual Block串联构成ResNet。

一个残差块有2条路径$F(x)$和$x$，$F(x)$路径拟合残差，不妨称之为残差路径，$x$路径为identity mapping恒等映射，称之为”shortcut”。图中的$\oplus$为element-wise addition，要求参与运算的$F(x)$和$x$的尺寸要相同。所以，随之而来的问题是，

• 残差路径如何设计？
• shortcut路径如何设计？
• Residual Block之间怎么连接？

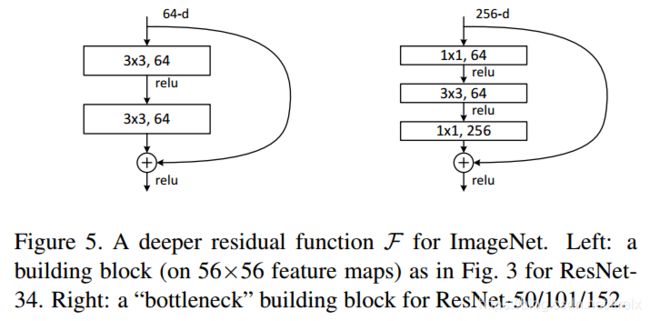
在原论文中，残差路径可以大致分成2种，一种有bottleneck结构，即下图右中的$1\times 1$ 卷积层，用于先降维再升维，主要出于降低计算复杂度的现实考虑，称之为“bottleneck block”，另一种没有bottleneck结构，如下图左所示，称之为“basic block”。basic block由2个$3\times 3$卷积层构成，bottleneck block由$1\times 1$

shortcut路径大致也可以分成2种，取决于残差路径是否改变了feature map数量和尺寸，一种是将输入$x$原封不动地输出，另一种则需要经过$1\times 1$卷积来升维 or/and 降采样，主要作用是将输出与$F(x)$路径的输出保持shape一致，对网络性能的提升并不明显，两种结构如下图所示，

至于Residual Block之间的衔接，在原论文中，$F(x)+x$经过$ReLU$后直接作为下一个block的输入$x$。

对于$F(x)$路径、shortcut路径以及block之间的衔接，在论文Identity Mappings in Deep Residual Networks中有更进一步的研究，具体在文章后面讨论。

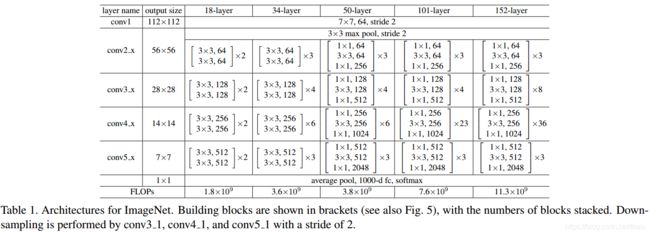
ResNet 网络结构

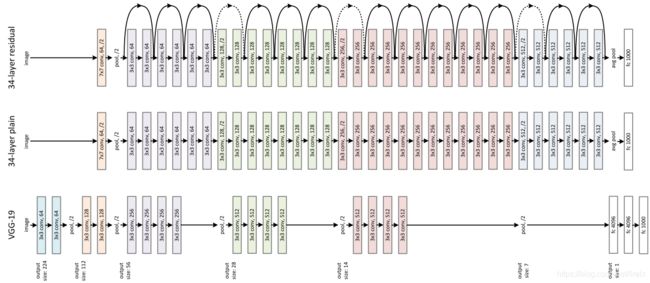
ResNet为多个Residual Block的串联，下面直观看一下ResNet-34与34-layer plain net和VGG的对比，以及堆叠不同数量Residual Block得到的不同ResNet。

ResNet的设计有如下特点：

• 与plain net相比，ResNet多了很多“旁路”，即shortcut路径，其首尾圈出的layers构成一个Residual Block；
• ResNet中，所有的Residual Block都没有pooling层，降采样是通过conv的stride实现的；
• 分别在conv3_1、conv4_1和conv5_1 Residual Block，降采样1倍，同时feature map数量增加1倍，如图中虚线划定的block；
• 通过Average Pooling得到最终的特征，而不是通过全连接层；
• 每个卷积层之后都紧接着BatchNorm layer，为了简化，图中并没有标出；

ResNet结构非常容易修改和扩展，通过调整block内的channel数量以及堆叠的block数量，就可以很容易地调整网络的宽度和深度，来得到不同表达能力的网络，而不用过多地担心网络的“退化”问题，只要训练数据足够，逐步加深网络，就可以获得更好的性能表现。

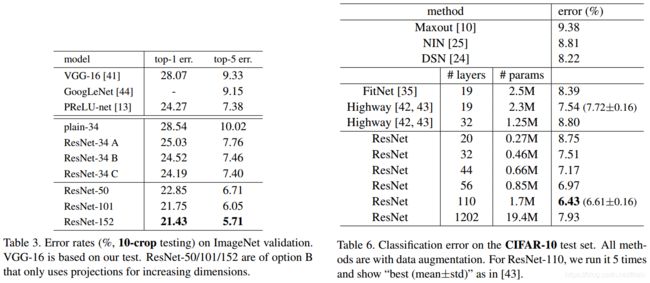
下面为网络的性能对比，

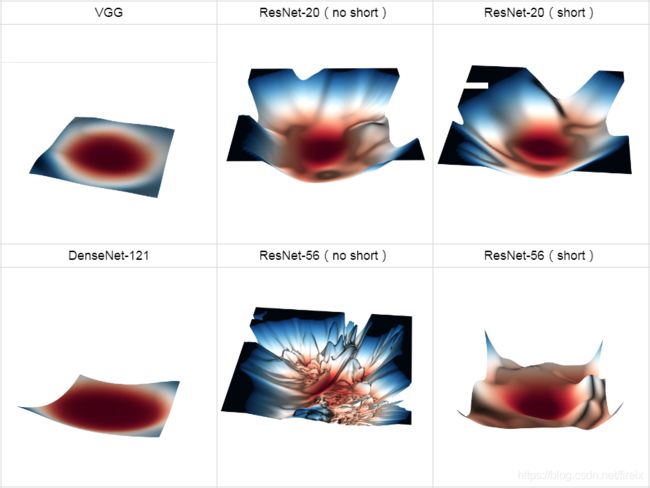
error surface对比

上面的实验说明，不断地增加ResNet的深度，甚至增加到1000层以上，也没有发生“退化”，可见Residual Block的有效性。ResNet的动机在于认为拟合残差比直接拟合潜在映射更容易优化，下面通过绘制error surface直观感受一下shortcut路径的作用，图片截自Loss Visualization。

可以发现：

• ResNet-20（no short）浅层plain net的error surface还没有很复杂，优化也会很困难，但是增加到56层后复杂程度极度上升。对于plain net，随着深度增加，error surface 迅速“恶化”；
• 引入shortcut后，error suface变得平滑很多，梯度的可预测性变得更好，显然更容易优化；

Residual Block的分析与改进

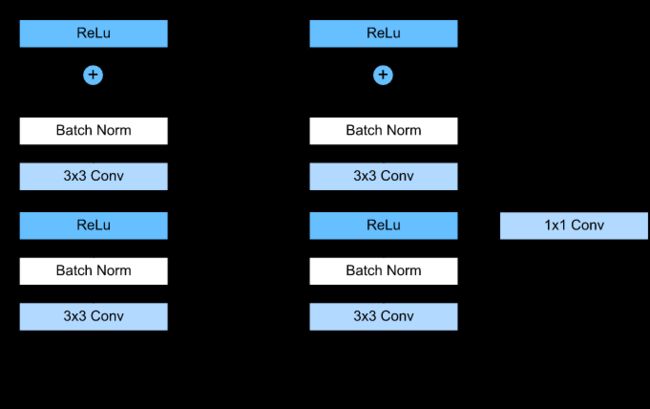
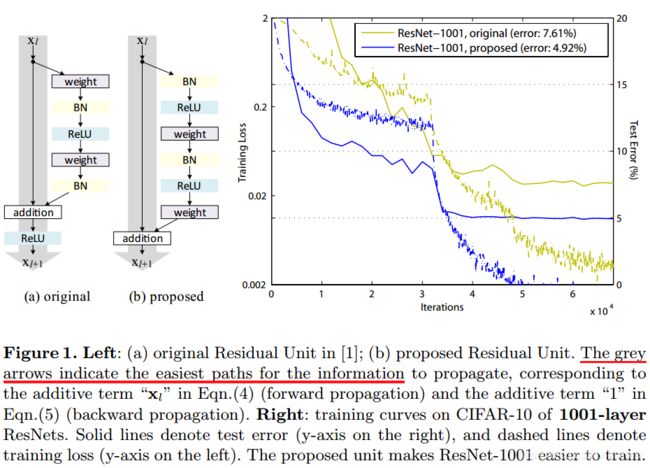
论文Identity Mappings in Deep Residual Networks进一步研究ResNet，通过ResNet反向传播的理论分析以及调整Residual Block的结构，得到了新的结构，如下

注意，这里的视角与之前不同，这里将shortcut路径视为主干路径，将残差路径视为旁路。

新提出的Residual Block结构，具有更强的泛化能力，能更好地避免“退化”，堆叠大于1000层后，性能仍在变好。具体的变化在于

• **通过保持shortcut路径的“纯净”，可以让信息在前向传播和反向传播中平滑传递，这点十分重要。**为此，如无必要，不引入$1\times 1$卷积等操作，同时将上图灰色路径上的ReLU移到了$F(x)$路径上。
• 在残差路径上，将BN和ReLU统一放在weight前作为pre-activation，获得了“Ease of optimization”以及“Reducing overfitting”的效果。

下面具体解释一下。

令$h(x_l)$为shortcut路径上的变换，$f$为addition之后的变换，原Residual Block中$f=ReLU$，当$h$和$f$均为恒等映射时，可以得到任意两层$x_L$和$x_l$之间的关系，此时信息可以在$x_l$和$x_L$间无损直达，如下前向传播中的$x_l$以及反向传播中的$1$。
y l = h ( x l ) + F ( x l , W l ) x l + 1 = f ( y l ) x l + 1 = x l + F ( x l , W l ) x L = x l + ∑ i = l L − 1 F ( x i , W i ) ∂ E ∂ x l = ∂ E ∂ x L ∂ x L ∂ x l = ∂ E ∂ x L ( 1 + ∂ ∂ x l ∑ i = l L − 1 F ( x i , W i ) ) \begin{aligned}\mathbf{y}_{l}&= h\left(\mathbf{x}_{l}\right)+\mathcal{F}\left(\mathbf{x}_{l}, \mathcal{W}_{l}\right) \\ \mathbf{x}_{l+1}&=f\left(\mathbf{y}_{l}\right) \\\mathbf{x}_{l+1}&=\mathbf{x}_{l}+\mathcal{F}\left(\mathbf{x}_{l}, \mathcal{W}_{l}\right) \\\mathbf{x}_{L}&=\mathbf{x}_{l}+\sum_{i=l}^{L-1} \mathcal{F}\left(\mathbf{x}_{i}, \mathcal{W}_{i}\right) \\\frac{\partial \mathcal{E}}{\partial \mathbf{x}_{l}}=\frac{\partial \mathcal{E}}{\partial \mathbf{x}_{L}} \frac{\partial \mathbf{x}_{L}}{\partial \mathbf{x}_{l}}&=\frac{\partial \mathcal{E}}{\partial \mathbf{x}_{L}}\left(1+\frac{\partial}{\partial \mathbf{x}_{l}} \sum_{i=l}^{L-1} \mathcal{F}\left(\mathbf{x}_{i}, \mathcal{W}_{i}\right)\right)\end{aligned} yl​xl+1​xl+1​xL​∂xl​∂E​=∂xL​∂E​∂xl​∂xL​​​=h(xl​)+F(xl​,Wl​)=f(yl​)=xl​+F(xl​,Wl​)=xl​+i=l∑L−1​F(xi​,Wi​)=∂xL​∂E​(1+∂xl​∂​i=l∑L−1​F(xi​,Wi​))​
反向传播中的这个$1$具有一个很好的性质，**任意两层间的反向传播，这一项都是$1$，可以有效地避免梯度消失和梯度爆炸。**如果$h$和$f$不是恒等映射，就会让这一项变得复杂，若是令其为一个大于或小于1的scale因子，反向传播连乘后就可能导致梯度爆炸或消失，层数越多越明显，这也是ResNet比highway network性能好的原因。需要注意的是，BN层解决了plain net的梯度消失和爆炸，这里的1可以避免short cut 路径上的梯度消失和爆炸。

shortcut路径将反向传播由连乘形式变为加法形式，让网络最终的损失在反向传播时可以无损直达每一个block，也意味着每个block的权重更新都部分地直接作用在最终的损失上。看上面前向传播的公式，可以看到某种ensemble形式，信息虽然可以在任意两层之间直达，但这种直达其实是隐含的，对某个block而言，它只能看到加法的结果，而不知道加法中每个加数是多数，从信息通路上讲尚不彻底——由此也诞生了DenseNet。

对于残差路径的改进，作者进行了不同的对比实验，最终得到了将BN和ReLU统一放在weight前的full pre-activation结构。

小结

ResNet的动机在于解决“退化”问题，残差块的设计让学习恒等映射变得容易，即使堆叠了过量的block，ResNet可以让冗余的block学习成恒等映射，性能也不会下降。所以，网络的“实际深度”是在训练过程中决定的，即ResNet具有某种深度自适应的能力。

深度自适应能解释不会“退化”，但为什么可以更好？

通过可视化error surface，我们看到了shortcut的平滑作用，但这只是结果，背后的根由是什么？

也许彻底搞懂ResNet还需要进一步地研究，但已有很多不同的理解角度，

• 微分方程的角度，A Proposal on Machine Learning via Dynamical Systems
• ensemble的角度，Residual Networks Behave Like Ensembles of Relatively Shallow Networks
• 信息/梯度通路的角度，Identity Mappings in Deep Residual Networks
• 类比泰勒展开、类比小波……

通过不同侧面尝试解释，能获得对ResNet更深刻更全面的认识，限于篇幅，本文不再展开。以上。

PS：实际是笔者还没整理出清晰完整的思路（逃

参考

• paper: Deep Residual Learning for Image Recognition
• paper: Identity Mappings in Deep Residual Networks
• Loss Visualization
• blog: ResNet, torchvision, bottlenecks, and layers not as they seem
• code: pytorch-resnet
• Residual Networks (ResNet)
• code: resnet-1k-layers/resnet-pre-act.lua