数据结构-树(一)
我们在前面讲解了排序算法的相关知识,现在来插入数据结构的相关内容。树是数据结构的三大结构之一。肯定是非常重要的。乃什么是树呢?树又是怎样的数据结构呢?树又分为哪些种类呢?我们接下来去探索下一!!!
目录
树的定义
树结点的分类
树结点之间的关系
树的层次
二叉树
定义
特点
基本形态
特殊情况
二叉树的性质
二叉树存储结构
二叉树的遍历
二分搜索树(BST)
添加元素
是否包含某元素
前序遍历(递归-迭代)
中序遍历(递归-迭代)
后序遍历(递归)
层次遍历(迭代)
查找最大值与最小值
删除最大值和最小值
判空和元素个数
toString()和iterator()
二分搜索树的完整代码
LinkedSet
完成代码
TreeSet
完整代码
测试LinkedSet与TreeSet
测试代码
运行结果
TreeMap
完整代码
测试代码
运行结果
AVLTreeMap
完整代码
测试代码
运行结果
树的定义
树(Tree)是n(n≥0)个结点的有限集。当n=0时称为空树。在任意一颗非空树中: (1)有且仅有一个特定的称为根(root)的结点; (2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、……、Tm,其中每一个集合本身又是一颗树,并且称为根的子树(SubTree)
树结点的分类
结点拥有的子树数称为结点的度(Degree)。度为0的结点称为叶节点(Leaf)或终端结点;度不为0的结点称为非终端结点或分支结点。除根节点外,分支结点也成为内部节点。树的度是树内各结点的度的最大值。
树结点之间的关系
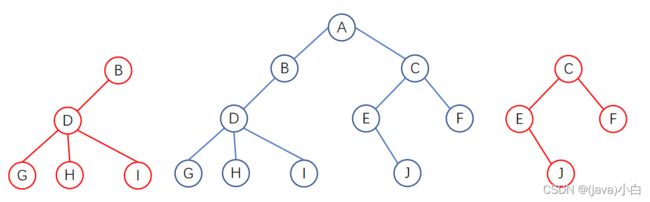
结点的子树的根称为该结点的孩子(Child),相应地,该结点称为孩子的双亲(Parent)。同一个双亲的孩子之间互称兄弟(Sibling)。结点的祖先是从根到该结点所经分支上的所有结点。以某结点为根的子树中任一结点都称为该结点的子孙。
对于如图 我们就可以简单的去解释一下:
(1)A是B,C的双亲
(2)B,C之间是兄弟
(3)D是B的孩子
(4)D和E之间是堂兄弟
(5)A,B,D是G的祖先
(6)其他都是A的子孙
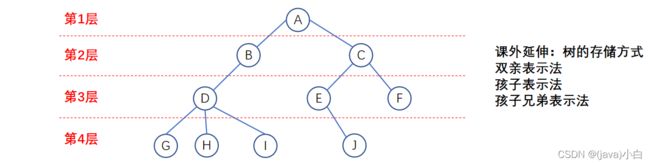
树的层次
结点的层次(Level)从根结点开始定义起,根为第一层,根的孩子为第二层。若某结点在第i层,则其子树的根就在i+1层。其双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度(Depth)或高度。
二叉树
定义
二叉树(Binary Tree)是n(n≥0)个结点的有限集合,该集合或者空集(称为空二叉树),或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
特点
(1)每个结点最多有两棵子树
(2)左子树和右子树是有顺序的
(3)即使树中某结点只有一棵子树,也要区分左右
基本形态
(1)空二叉树
(2)只有一个根节点
(3)根节点只有左子树
(4)根节点只有右子树
(5)根节点既有左子树又有右子树
特殊情况
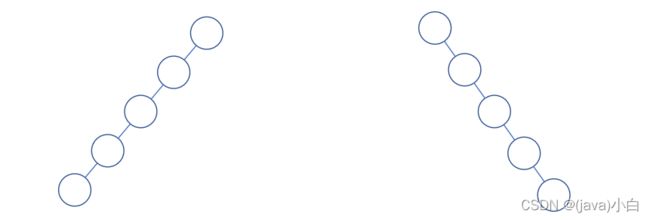
斜树
所有的结点都只有左子树的二叉树叫左斜树。所有结点都只有右子树的二叉树叫右斜树 所以在极端情况下二叉树会退化成线性表(线性表是树的特殊表现形式),这种情况也称之为非平衡树
满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树 满二叉树是一种平衡二叉树
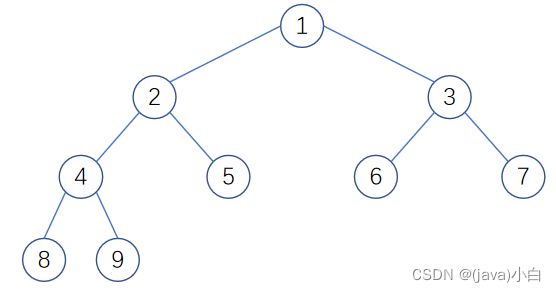
完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1≤i≤n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这颗二叉树称为完全二叉树 完全二叉树也是一种平衡二叉树
特点
(1)叶子节点只能出现在最下两层 (2)最下层的叶子一定集中在左部连续位置 (3)倒数二层,若有叶子结点,一定都在右部连续位置 (4)如果结点度为1,则该结点只有左孩子 (5)同样结点个数的二叉树,完全二叉树的深度最小
二叉树的性质
(1)在二叉树的第i层上至多有2^ⅈ−1个结点(i≥1) (2)深度为k的二叉树至多有2^k−1个结点(k≥1) (3)对任何一棵二叉树 如果终端结点数为n_0,度为2的结点数为n_2 则n_0= n_2+1 (4)具有n个结点的完全二叉树的深度为⌊log_2n⌋+1 (5)如果对于一棵有n个结点的完全二叉树的结点按层序编号 如果i=1,结点无双亲;如果i>1,则双亲是⌊i/2⌋ 如果2i>n,则结点i无左孩子;否则其左孩子为2i 如果2i+1>n,则结点i无右孩子;否则有孩子为2i+1
二叉树存储结构
顺序存储结构
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现出之间的逻辑关系。
链式存储结构
二叉树每个结点最多有两个孩子,所以设计为一个数据域和两个指针域的结点进行链接,这种链表也叫作二叉链表
二叉树的遍历
主要分为两类:深度优先遍历DFS和广度优先遍历BFS
深优:前序遍历,中序遍历,后序遍历 广优:层序遍历
我们上面讲解了树的相关概念。我们现在来讲解一下二分搜索树(Binary Search Tree)。那什么是二分搜索树呢?
二分搜索树(BST)
本身是二叉树,只不过对于二分搜索树的每个结点而言 大于其左子树的所有结点的值 小于其右子树的所有结点的值 同样,其子树也是一颗二分搜索树 那么该树中元素要具有可比性 不包含重复元素
我们现在用代码实现,因为在添加 删除等操作时所传入的结点数据域的类型不一定是整数,所以我们的数据类型得是具有可比较能力的。因为树也是由结点来连接而成,简单来说结点是一个单位。所以我们先要创建一个结点类,并且要编写相关属性。
//定义二分搜索树的结点信息
private class Node {
public E e; //数据域
public Node left; //左孩子(当前Node结点左子树的根)
public Node right; //右孩子(当前Node结点右子树的根)
public Node(E e) {
this.e = e;
left = null;
right = null;
}
@Override
public String toString() {
return e.toString();
}
}
private Node root; //根节点的指针 根指针 采用真实根节点 如果二分搜索树为空 root == null
private int size; //二分搜索树中元素的个数(结点的个数)
public BinarySearchTree(){
root = null;
size = 0;
}添加元素
我们可以通过迭代和递归两种思路来完成。
迭代思路
Node node = new Node(e);
if (isEmpty()) {
root = node;
size++;
}
Node cur = root;
while (true) {
//新元素比当前大 往右走
if (node.e.compareTo(cur.e) > 0) {
if (cur.right == null) {
cur.right = node;
size++;
break;
} else {
cur = cur.right;
}
//新元素比当前小 往左走
} else if (node.e.compareTo(cur.e) < 0) {
if (cur.left == null) {
cur.left = node;
size++;
break;
} else {
cur = cur.left;
}
} else {
break;
}
}递归思路
root = add(root,e);
}
//在以node为根的树中 插入元素e 并返回新树的根
private Node add(Node node, E e) {
//从下一层向上一层
if (node == null){
size++;
return new Node(e);
}
//当前层向下一层
if (e.compareTo(node.e) < 0){
node.left = add(node.left,e);
}else if (e.compareTo(node.e) > 0){
node.right = add(node.right,e);
}
//当前层向上一层
return node;
}是否包含某元素
迭代思路
//迭代思路
Node cur = root ;
while (true){
if (e.compareTo(cur.e) < 0){
if (cur.left == null){
return false;
}
cur = cur.left;
}else if (e.compareTo(cur.e) > 0){
if (cur.right == null){
return false;
}
cur = cur.right;
}else {
return true;
}
}递归思路
return contains(root,e);
}
//查看以nide为根的二分搜索树中是否包含元素e
private boolean contains(Node node, E e) {
if (node == null){
return false;
}
if (e.compareTo(node.e) < 0){
return contains(node.left,e);
}else if (e.compareTo(node.e) > 0){
return contains(node.right,e);
}else {
return true;
}
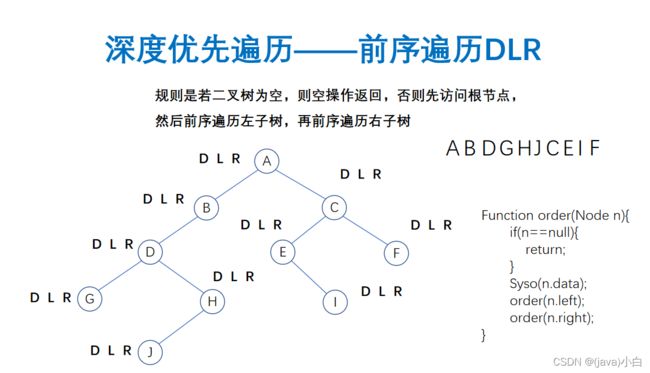
}前序遍历(递归-迭代)
在这里肯定递归比迭代的代码简单,但是递归还是需要大家去思考.
//前序遍历
public void preOrder(){
preOrder(root);
}
//前序遍历-递归方式 以node为根节点 前序遍历DLR
private void preOrder(Node node) {
if (node == null){
return;
}
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
//前序遍历-迭代方式
public void preOrderNR(){
LinkedList stack = new LinkedList<>();
if (isEmpty()){
return;
}
stack.push(root);
while (!stack.isEmpty()){
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null){
stack.push(cur.right);
}
if (cur.left != null ){
stack.push(cur.left);
}
}
} 中序遍历(递归-迭代)
//中序遍历-向外提供
public void inOrder() {
inOrder(root);
}
//中序遍历-递归方式 以node为根节点 中序遍历LDR
private void inOrder(Node node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
//中序遍历-迭代方式
public void inOrderNR(){
LinkedList stack = new LinkedList<>();
Node p = root;
while (p != null){
stack.push(p);
p = p.left;
}
while (!stack.isEmpty()){
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null){
Node n = cur.right;
while (n != null){
stack.push(n);
n = n.left;
}
}
}
} 后序遍历(递归)
//后序遍历
public void postOrder(){
postOrder(root);
}
//后序遍历-递归方式 以node为根节点 后序遍历LDR
private void postOrder(Node node) {
if (node == null){
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
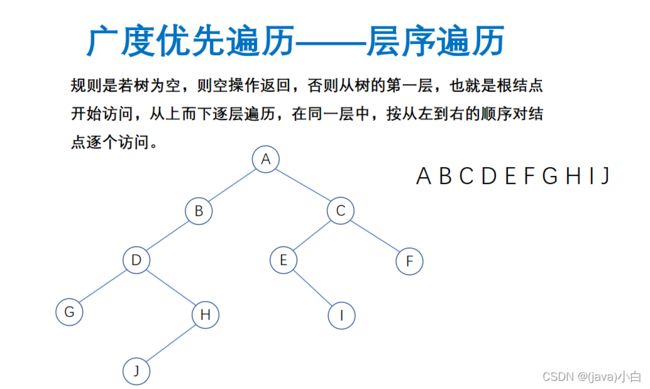
}层次遍历(迭代)
//层次遍历-迭代方式
public void levelOrder(){
LinkedList queue = new LinkedList<>();
if (isEmpty()){
return;
}
queue.offer(root);
while (!queue.isEmpty()){
Node cur = queue.poll();
System.out.println(cur.e);
if (cur.left != null){
queue.offer(cur.left);
}
if (cur.right != null){
queue.offer(cur.right);
}
}
} 查找最大值与最小值
采用递归查找最小值
//查找最小值-递归
public E minimum(){
if (root == null){
throw new IllegalArgumentException("bst is empty");
}
return minimum(root).e;
}
private Node minimum(Node node){
if (node.left == null){
return node;
}
return minimum(node.left);
}采用递归查找最大值
//查找最大值-递归
public E maximum(){
if (root == null){
throw new IllegalArgumentException("bst is empty");
}
return maximum(root).e;
}
private Node maximum(Node node){
if (node.right == null){
return node;
}
return maximum(node.right);
}
删除最大值和最小值
删除最小值
//删除最小值
public E removeMin(){
E ret = minimum();
root = removeMin(root);
return ret;
}
//以node为根 删除其中的最小值节点 返回删除后的新树的根
private Node removeMin(Node node){
if (node.left == null){
Node rigthNode = node.right;
node.right = null;
size--;
return rigthNode;
}
node.left = removeMin(node.left);
return node;
}删除最大值
//删除最大值
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
//以node为根 删除其中的最大值节点 返回删除后的新树的根
private Node removeMax(Node node){
if (node.right == null){
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}删除任意元素
//随意删除元素
public void remove(E e){
root = remove(root,e);
}
//以node为根 删除元素e 并返回删除后的新树的根
//如果存在重复 删除的时候就要考虑当前节点出现的次数node.count--
private Node remove(Node node, E e) {
if (node == null){
return null;
}
if (e.compareTo(node.e) < 0){
node.left = remove(node.left,e);
return node;
}else if (e.compareTo(node.right.e) > 0){
node.right = remove(node.right,e);
return node;
}else { // 找到了
/*
if(node.count > 1){
node.count--;
}
*/
//如果待删除的节点左边为空 则右子树直接上
if(node.left == null){
Node rightNode = node.right;//此时右边可能为空 可能非空
node.right = null;
size--;
return rightNode;
}
if (node.right == null){
Node leftNode = node.left; // 此时左边非空
node.left = null;
size--;
return leftNode;
}
//左右都不不为空 把右子树的最小值当成新树的根返回
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
node.left = node.right = null;
return successor;
}
}判空和元素个数
public int size() {
return size;
}
public boolean isEmpty() {
return root == null && size == 0;
}
toString()和iterator()
@Override
public String toString() {
StringBuilder sb = new StringBuilder("[");
if (isEmpty()) {
sb.append(']');
} else {
Iterator it = iterator();
for (int i = 0; i < size; i++) {
sb.append(it.next());
if (i == size - 1) {
sb.append(']');
} else {
sb.append(',');
}
}
// while (it.hasNext()) {
// sb.append(it.next());
// sb.append(',');
// }
// sb.deleteCharAt(sb.length() - 1);
// sb.append(']');
}
return sb.toString();
}
@Override
public Iterator iterator() {
return new BinarySearchTreeIterator();
}
private class BinarySearchTreeIterator implements Iterator {
private Iterator it;
public BinarySearchTreeIterator() {
LinkedList list = new LinkedList<>();
LinkedList stack = new LinkedList<>();
Node p = root;
while (p != null) {
stack.push(p);
p = p.left;
}
while (!stack.isEmpty()) {
Node cur = stack.pop();
list.offer(cur.e);
if (cur.right != null) {
Node n = cur.right;
while (n != null) {
stack.push(n);
n = n.left;
}
}
}
it = list.iterator();
}
@Override
public boolean hasNext() {
return it.hasNext();
}
@Override
public E next() {
return it.next();
}
} 二分搜索树的完整代码
package p6.树与哈希表;
import P3.链式结构.LinkedList;
import java.util.Iterator;
//树与哈希表
public class BinarySearchTree> implements Iterable{
//定义二分搜索树的结点信息
private class Node {
public E e; //数据域
public Node left; //左孩子(当前Node结点左子树的根)
public Node right; //右孩子(当前Node结点右子树的根)
public Node(E e) {
this.e = e;
left = null;
right = null;
}
@Override
public String toString() {
return e.toString();
}
}
private Node root; //根节点的指针 根指针 采用真实根节点 如果二分搜索树为空 root == null
private int size; //二分搜索树中元素的个数(结点的个数)
public BinarySearchTree(){
root = null;
size = 0;
}
public void add(E e) {
/*
//添加的迭代思路
Node node = new Node(e);
if (isEmpty()) {
root = node;
size++;
}
Node cur = root;
while (true) {
//新元素比当前大 往右走
if (node.e.compareTo(cur.e) > 0) {
if (cur.right == null) {
cur.right = node;
size++;
break;
} else {
cur = cur.right;
}
//新元素比当前小 往左走
} else if (node.e.compareTo(cur.e) < 0) {
if (cur.left == null) {
cur.left = node;
size++;
break;
} else {
cur = cur.left;
}
} else {
break;
}
}
*/
root = add(root,e);
}
//在以node为根的树中 插入元素e 并返回新树的根
private Node add(Node node, E e) {
//从下一层向上一层
if (node == null){
size++;
return new Node(e);
}
//当前层向下一层
if (e.compareTo(node.e) < 0){
node.left = add(node.left,e);
}else if (e.compareTo(node.e) > 0){
node.right = add(node.right,e);
}
//当前层向上一层
return node;
}
public boolean contains(E e){
/*
//迭代思路
Node cur = root ;
while (true){
if (e.compareTo(cur.e) < 0){
if (cur.left == null){
return false;
}
cur = cur.left;
}else if (e.compareTo(cur.e) > 0){
if (cur.right == null){
return false;
}
cur = cur.right;
}else {
return true;
}
}
*/
return contains(root,e);
}
//查看以nide为根的二分搜索树中是否包含元素e
private boolean contains(Node node, E e) {
if (node == null){
return false;
}
if (e.compareTo(node.e) < 0){
return contains(node.left,e);
}else if (e.compareTo(node.e) > 0){
return contains(node.right,e);
}else {
return true;
}
}
//前序遍历
public void preOrder(){
preOrder(root);
}
//前序遍历-递归方式 以node为根节点 前序遍历DLR
private void preOrder(Node node) {
if (node == null){
return;
}
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
//前序遍历-迭代方式
public void preOrderNR(){
LinkedList stack = new LinkedList<>();
if (isEmpty()){
return;
}
stack.push(root);
while (!stack.isEmpty()){
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null){
stack.push(cur.right);
}
if (cur.left != null ){
stack.push(cur.left);
}
}
}
//中序遍历-向外提供
public void inOrder() {
inOrder(root);
}
//中序遍历-递归方式 以node为根节点 中序遍历LDR
private void inOrder(Node node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
//中序遍历-迭代方式
public void inOrderNR(){
LinkedList stack = new LinkedList<>();
Node p = root;
while (p != null){
stack.push(p);
p = p.left;
}
while (!stack.isEmpty()){
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null){
Node n = cur.right;
while (n != null){
stack.push(n);
n = n.left;
}
}
}
}
//后序遍历
public void postOrder(){
postOrder(root);
}
//后序遍历-递归方式 以node为根节点 后序遍历LDR
private void postOrder(Node node) {
if (node == null){
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
//层次遍历-迭代方式
public void levelOrder(){
LinkedList queue = new LinkedList<>();
if (isEmpty()){
return;
}
queue.offer(root);
while (!queue.isEmpty()){
Node cur = queue.poll();
System.out.println(cur.e);
if (cur.left != null){
queue.offer(cur.left);
}
if (cur.right != null){
queue.offer(cur.right);
}
}
}
//查找最小值-递归
public E minimum(){
if (root == null){
throw new IllegalArgumentException("bst is empty");
}
return minimum(root).e;
}
private Node minimum(Node node){
if (node.left == null){
return node;
}
return minimum(node.left);
}
//查找最大值-递归
public E maximum(){
if (root == null){
throw new IllegalArgumentException("bst is empty");
}
return maximum(root).e;
}
private Node maximum(Node node){
if (node.right == null){
return node;
}
return maximum(node.right);
}
//删除最小值
public E removeMin(){
E ret = minimum();
root = removeMin(root);
return ret;
}
//以node为根 删除其中的最小值节点 返回删除后的新树的根
private Node removeMin(Node node){
if (node.left == null){
Node rigthNode = node.right;
node.right = null;
size--;
return rigthNode;
}
node.left = removeMin(node.left);
return node;
}
//删除最大值
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
//以node为根 删除其中的最大值节点 返回删除后的新树的根
private Node removeMax(Node node){
if (node.right == null){
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
//随意删除元素
public void remove(E e){
root = remove(root,e);
}
//以node为根 删除元素e 并返回删除后的新树的根
//如果存在重复 删除的时候就要考虑当前节点出现的次数node.count--
private Node remove(Node node, E e) {
if (node == null){
return null;
}
if (e.compareTo(node.e) < 0){
node.left = remove(node.left,e);
return node;
}else if (e.compareTo(node.right.e) > 0){
node.right = remove(node.right,e);
return node;
}else { // 找到了
/*
if(node.count > 1){
node.count--;
}
*/
//如果待删除的节点左边为空 则右子树直接上
if(node.left == null){
Node rightNode = node.right;//此时右边可能为空 可能非空
node.right = null;
size--;
return rightNode;
}
if (node.right == null){
Node leftNode = node.left; // 此时左边非空
node.left = null;
size--;
return leftNode;
}
//左右都不不为空 把右子树的最小值当成新树的根返回
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
node.left = node.right = null;
return successor;
}
}
public int size() {
return size;
}
public boolean isEmpty() {
return root == null && size == 0;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder("[");
if (isEmpty()) {
sb.append(']');
} else {
Iterator it = iterator();
for (int i = 0; i < size; i++) {
sb.append(it.next());
if (i == size - 1) {
sb.append(']');
} else {
sb.append(',');
}
}
// while (it.hasNext()) {
// sb.append(it.next());
// sb.append(',');
// }
// sb.deleteCharAt(sb.length() - 1);
// sb.append(']');
}
return sb.toString();
}
@Override
public Iterator iterator() {
return new BinarySearchTreeIterator();
}
private class BinarySearchTreeIterator implements Iterator {
private Iterator it;
public BinarySearchTreeIterator() {
LinkedList list = new LinkedList<>();
LinkedList stack = new LinkedList<>();
Node p = root;
while (p != null) {
stack.push(p);
p = p.left;
}
while (!stack.isEmpty()) {
Node cur = stack.pop();
list.offer(cur.e);
if (cur.right != null) {
Node n = cur.right;
while (n != null) {
stack.push(n);
n = n.left;
}
}
}
it = list.iterator();
}
@Override
public boolean hasNext() {
return it.hasNext();
}
@Override
public E next() {
return it.next();
}
}
} 上述讲解完二分搜索树 ,我们可以利用才写一个集合(链式结构和树形结构)
存储不重复元素的容器 由链表实现 LinkedSet 有序 由二分搜索树实现 TreeSet 有序 自然排序 由哈希表实现 HashSet 无序
首先得定义Set接口
package p1.接口;
//底层可以用三种方式实现 linkSet bstSet HashSet
public interface Set extends Iterable {
public void add(E e);
public void remove(E e);
public boolean contains(E e);
public int size();
public boolean isEmpty();
}
LinkedSet
完成代码
package p6.树与哈希表;
import p1.接口.Set;
import P3.链式结构.LinkedList;
import java.util.Iterator;
//底层由链表来实现的集合
public class LinkedSet implements Set {
private LinkedList list;
public LinkedSet() {
list = new LinkedList<>();
}
@Override
public void add(E e) { //O(n)
if (!list.contains(e)) {
list.add(e);
}
}
@Override
public void remove(E e) { //O(n)
list.remove(e);
}
@Override
public boolean contains(E e) { //O(n)
return list.contains(e);
}
@Override
public int size() {
return list.size();
}
@Override
public boolean isEmpty() {
return list.isEmpty();
}
@Override
public String toString() {
return list.toString();
}
@Override
public Iterator iterator() {
return list.iterator();
}
} TreeSet
完整代码
package p6.树与哈希表;
import p1.接口.Set;
import java.util.Iterator;
//底层由二分搜索树BinarySearchTree(BST)实现的集合
public class TreeSet> implements Set {
private BinarySearchTree bst;
public TreeSet() {
bst = new BinarySearchTree<>();
}
@Override
public void add(E e) { //O(logn)
bst.add(e);
}
@Override
public void remove(E e) { //O(logn)
bst.remove(e);
}
@Override
public boolean contains(E e) { //O(logn)
return bst.contains(e);
}
@Override
public int size() {
return bst.size();
}
@Override
public boolean isEmpty() {
return bst.isEmpty();
}
@Override
public String toString() {
return bst.toString();
}
@Override
public Iterator iterator() {
return bst.iterator();
}
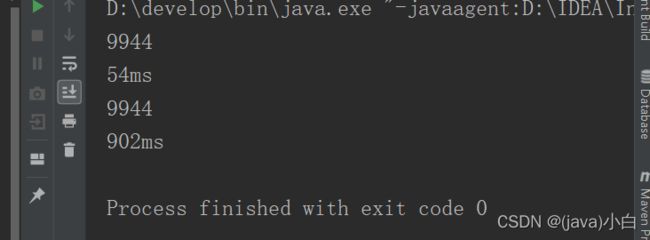
} 测试LinkedSet与TreeSet
测试代码
用英文文章来测试单词的个数等
package p0.测试;
import p6.树与哈希表.FileOperation;
import p6.树与哈希表.LinkedSet;
import p6.树与哈希表.TreeSet;
import java.util.ArrayList;
public class TestBSTSetAndLinkedSet {
public static void main(String[] args) {
ArrayList words = new ArrayList<>();
//把文本文件中所有的英文单词统计在words这个线性表中(所有单词 包含重复)
FileOperation.readFile("D:\\IDEA\\DataSAlgorithms\\a-tale-of-two-cities.txt", words);
testTreeSet(words);
testLinkedSet(words);
}
private static void testLinkedSet(ArrayList words) {
Long startTime = System.currentTimeMillis();
LinkedSet set = new LinkedSet<>();
for (String word : words) {
set.add(word); //把所有单词统计到集合中 每个单词只出现一次
}
Long endTime = System.currentTimeMillis();
System.out.println(set.size());
System.out.println(endTime - startTime + "ms");
}
private static void testTreeSet(ArrayList words) {
Long startTime = System.currentTimeMillis();
TreeSet set = new TreeSet<>();
for (String word : words) {
set.add(word); //把所有单词统计到集合中 每个单词只出现一次
}
Long endTime = System.currentTimeMillis();
System.out.println(set.size());
System.out.println(endTime - startTime + "ms");
}
} 运行结果
我们上面定义完Set集合,不能忘了还有映射关系Map;首先得定义Map接口;
Map接口
package p1.接口;
public interface Map{
//将键值对key-value加入映射 如果已存在则为修改
public void put(K key, V value);
//删除指定key的键值对 并返回对应的值value
public V remove(K key);
//查找指定key对应的键值对是否存在
public boolean contains(K key);
//获取指定key对应的值value
public V get(K key);
//修改指定key处的值为新的value
public void set(K key, V value);
public int size();
public boolean isEmpty();
//获取所有键的Set
public Set keySet();
//获取所有值的List
public List values();
//获取所有键值对的Set
public Set> entrySet();
public interface Entry extends Comparable> {
public K getKey();
public V getValue();
}
} TreeMap
完整代码
package p6.树与哈希表;
import p1.接口.List;
import p1.接口.Map;
import p1.接口.Set;
import P3.链式结构.LinkedList;
import java.util.Iterator;
public class TreeMap,V> implements Map,Iterable> {
//定义二分搜索树的结点信息
private class Node {
public K key; //键
public V value; //值
public Node left;
public Node right;
public Node() {}
public Node(K key, V value) {
this.key = key;
this.value = value;
}
}
private Node root;
private int size;
public TreeMap() {
root = null;
size = 0;
}
//辅助函数 获取指定key所在的结点
//以node为根的二分搜索树中 查找key所在的结点 - 递归
private Node getNode(Node node, K key) {
if (node == null) {
return null;
}
if (key.compareTo(node.key) < 0) {
return getNode(node.left, key);
} else if (key.compareTo(node.key) > 0) {
return getNode(node.right, key);
} else {
return node;
}
}
@Override
public void put(K key, V value) {
root = put(root, key, value);
}
private Node put(Node node, K key, V value) {
if (node == null) {
size++;
return new Node(key,value);
}
if (key.compareTo(node.key) < 0) {
node.left = put(node.left, key,value);
} else if (key.compareTo(node.key) > 0) {
node.right = put(node.right, key,value);
} else { //如果已经存在 则put为修改
node.value = value;
}
return node;
}
@Override
public V remove(K key) {
Node delNode = getNode(root,key);
if (delNode != null) {
root = remove(root,key);
return delNode.value;
}
return null;
}
private Node remove(Node node, K key) {
if (node == null) {
return null;
}
if (key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
return node;
} else if (key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
return node;
} else {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
private Node removeMin(Node node) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
private Node minimum(Node node) {
if (isEmpty()) {
return null;
}
if (node.left == null) {
return node;
}
return minimum(node.left);
}
@Override
public boolean contains(K key) {
return getNode(root,key) != null;
}
@Override
public V get(K key) {
Node node = getNode(root,key);
if (node != null) {
return node.value;
}
return null;
}
@Override
public void set(K key, V value) {
Node node = getNode(root,key);
if (node == null) {
throw new IllegalArgumentException("key-value is not exist");
}
node.value = value;
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0 && root == null;
}
//获取所有键的Set
@Override
public Set keySet() {
TreeSet set = new TreeSet<>();
inOrderKetSet(root, set);
return set;
}
private void inOrderKetSet(Node node, TreeSet set) {
if (node == null) {
return;
}
inOrderKetSet(node.left,set);
set.add(node.key);
inOrderKetSet(node.right,set);
}
//获取所有值的List
@Override
public List values() {
LinkedList list = new LinkedList<>();
inOrderValues(root, list);
return list;
}
private void inOrderValues(Node node, LinkedList list) {
if (node == null) {
return;
}
inOrderValues(node.left, list);
list.add(node.value);
inOrderValues(node.right, list);
}
@Override
public Set> entrySet() {
TreeSet> entries = new TreeSet<>();
inOrderEntrys(root,entries);
return entries;
}
private void inOrderEntrys(Node node, TreeSet> entries) {
if (node == null) {
return;
}
inOrderEntrys(node.left,entries);
entries.add(new BSTEntry<>(node.key, node.value));
inOrderEntrys(node.right,entries);
}
//自己实现
@Override
public String toString() {
return null;
}
//自己实现
@Override
public Iterator> iterator() {
return null;
}
//键值对对象
private class BSTEntry,V> implements Entry {
private K key;
private V value;
public BSTEntry(K key, V value) {
this.key = key;
this.value = value;
}
@Override
public K getKey() {
return key;
}
@Override
public V getValue() {
return value;
}
@Override
public String toString() {
return key + ":" + value;
}
@Override
public int compareTo(Entry o) {
return this.getKey().compareTo(o.getKey()) ;
}
}
}
测试代码
package p0.测试;
import p6.树与哈希表.FileOperation;
import p6.树与哈希表.TreeMap;
import java.util.ArrayList;
public class TestTreeMap {
public static void main(String[] args) {
TreeMap map = new TreeMap<>();
map.put(12,"xixi");
map.put(10,"haha");
map.put(9,"baba");
map.put(13,"lala");
System.out.println(map.keySet());
System.out.println(map.values());
System.out.println(map.entrySet());
TreeMap map2 = new TreeMap<>();
ArrayList words = new ArrayList<>();
FileOperation.readFile("D:\\IDEA\\DataSAlgorithms\\a-tale-of-two-cities.txt",words);
for (String word : words) {
if (map2.contains(word)) {
map2.set(word,map2.get(word) + 1);
} else {
map2.put(word,1);
}
}
System.out.println(map2.size());
System.out.println(map2.get("the"));
System.out.println(map2.get("if"));
}
} 运行结果
AVLTreeMap
完整代码
package p6.树与哈希表;
import p1.接口.List;
import p1.接口.Map;
import p1.接口.Set;
import p2.线性结构.ArrayList;
import P3.链式结构.LinkedList;
//AVL平衡二分搜索树实现的映射
public class AVLTreeMap,V> implements Map {
private class Node {
public K key; //键
public V value; //值
public int height; //高度
public Node left;
public Node right;
public Node (K key, V value) {
this.key = key;
this.value = value;
left = null;
right = null;
height = 1; //新结点的高度默认都是1
}
}
private Node root;
private int size;
public AVLTreeMap() {
root = null;
size = 0;
}
//以node为根的子树中 查找key所在的结点
private Node getNode(Node node, K key) {
if(node == null) {
return null;
}
if (key.compareTo(node.key) < 0) {
return getNode(node.left, key);
} else if (key.compareTo(node.key) > 0) {
return getNode(node.right, key);
} else {
return node;
}
}
//获取某一个结点的高度 如果该结点为空 则高度为0
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
//计算某一个结点的平衡因子(左右子树的高度差) >0左边高 ==0左右同高 <0右边高
private int getBalanceFactor(Node node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
//验证是否是二分搜索树
public boolean isBST() {
ArrayList list = new ArrayList<>();
inOrderKeys(root, list);
for (int i = 1; i < list.size(); i++) {
if (list.get(i - 1).compareTo(list.get(i)) > 0) {
return false;
}
}
return true;
}
private void inOrderKeys(Node node, ArrayList list) {
if (node == null) {
return;
}
inOrderKeys(node.left, list);
list.add(node.key);
inOrderKeys(node.right,list);
}
//验证得是一颗平衡树
public boolean isBalanced() {
return isBalanced(root);
}
private boolean isBalanced(Node node) {
if (node == null) {
return true;
}
int balancedFactor = getBalanceFactor(node);
if (Math.abs(balancedFactor) > 1) {
return false;
}
return isBalanced(node.left) && isBalanced(node.right);
}
//左旋转(右侧的右侧) 将y结点进行左旋转 并返回新的根
private Node leftRotate(Node y) {
Node x = y.right;
Node T3 = x.left;
x.left = y;
y.right = T3;
y.height = Math.max(getHeight(y.left),getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left),getHeight(x.right)) + 1;
return x;
}
//右旋转(左侧的左侧) 将y结点进行右旋转 并返回新的根
private Node rightRotate(Node y) {
Node x = y.left;
Node T3 = x.right;
x.right = y;
y.left = T3;
y.height = Math.max(getHeight(y.left),getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left),getHeight(x.right)) + 1;
return x;
}
@Override
public void put(K key, V value) {
root = put(root,key, value);
}
private Node put(Node node, K key, V value) {
if (node == null) {
size++;
return new Node(key, value);
}
if (key.compareTo(node.key) < 0) {
node.left = put(node.left, key, value);
} else if (key.compareTo(node.key) > 0) {
node.right = put(node.right, key,value);
} else {
node.value = value;
}
//当前结点的高度需要更新
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
//判断当前结点是否是平衡的
int balanceFactor = getBalanceFactor(node);
// >1说明当前结点左侧不平衡 node.left >= 0 左侧的左侧不平衡
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
return rightRotate(node);
}
// >1说明当前结点左侧不平衡 node.left < 0 左侧的右侧不平衡
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// <-1说明当前结点右侧不平衡 node.right >= 0 右侧的左侧不平衡
if (balanceFactor < -1 && getBalanceFactor(node.right) >= 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
// <-1说明当前结点右侧不平衡 node.right < 0 右侧的右侧不平衡
if (balanceFactor < -1 && getBalanceFactor(node.right) < 0) {
return leftRotate(node);
}
return node;
}
@Override
public V remove(K key) {
Node delNode = getNode(root,key);
if (delNode != null) {
root = remove(root,key);
return delNode.value;
}
return null;
}
private Node remove(Node node, K key) {
if (node == null) {
return null;
}
Node retNode = null;
if (key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
retNode = node;
} else if (key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
retNode = node;
} else { //找到了要删除的结点
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
retNode = rightNode;
} else if (node.right == null) {
Node leftNode = node.left;
node.left = null;
retNode = leftNode;
} else {
Node successor = minmum(node.right);
successor.right = remove(node.right,successor.key);
successor.left = node.left;
node.left = node.right = null;
retNode = successor;
}
}
if (retNode == null) {
return retNode;
}
//更新高度
retNode.height = Math.max(getHeight(retNode.left), getHeight(retNode.right)) + 1;
//获取平衡因子判断是否需要自平衡
int balanceFactor = getBalanceFactor(retNode);
// >1说明当前结点左侧不平衡 node.left >= 0 左侧的左侧不平衡
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
return rightRotate(retNode);
}
// >1说明当前结点左侧不平衡 node.left < 0 左侧的右侧不平衡
if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left);
return rightRotate(retNode);
}
// <-1说明当前结点右侧不平衡 node.right >= 0 右侧的左侧不平衡
if (balanceFactor < -1 && getBalanceFactor(retNode.right) >= 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
// <-1说明当前结点右侧不平衡 node.right < 0 右侧的右侧不平衡
if (balanceFactor < -1 && getBalanceFactor(retNode.right) < 0) {
return leftRotate(retNode);
}
return retNode;
}
private Node minmum(Node node) {
if (node.left == null) {
return node;
} else {
return minmum(node.left);
}
}
@Override
public boolean contains(K key) {
return getNode(root,key) != null;
}
@Override
public V get(K key) {
Node node = getNode(root,key);
if (node != null) {
return node.value;
}
return null;
}
@Override
public void set(K key, V value) {
Node node = getNode(root,key);
if (node == null) {
throw new IllegalArgumentException("key-value is not exist");
}
node.value = value;
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0 && root == null;
}
@Override
public Set keySet() {
TreeSet set = new TreeSet<>();
inOrderKeySet(root, set);
return set;
}
private void inOrderKeySet(Node node, TreeSet set) {
if (node == null) {
return;
}
inOrderKeySet(node.left,set);
set.add(node.key);
inOrderKeySet(node.right,set);
}
@Override
public List values() {
LinkedList list = new LinkedList<>();
inOrderValues(root, list);
return list;
}
private void inOrderValues(Node node, LinkedList list) {
if (node == null) {
return;
}
inOrderValues(node.left, list);
list.add(node.value);
inOrderValues(node.right, list);
}
@Override
public Set> entrySet() {
TreeSet> entries = new TreeSet<>();
inOrderEntrys(root,entries);
return entries;
}
private void inOrderEntrys(Node node, TreeSet> entries) {
if (node == null) {
return;
}
inOrderEntrys(node.left, entries);
entries.add(new BSTEntry<>(node.key, node.value));
inOrderEntrys(node.right, entries);
}
//键值对对象
private class BSTEntry,V> implements Entry {
private K key;
private V value;
public BSTEntry(K key, V value) {
this.key = key;
this.value = value;
}
@Override
public K getKey() {
return key;
}
@Override
public V getValue() {
return value;
}
@Override
public String toString() {
return key + ":" + value;
}
@Override
public int compareTo(Entry o) {
return this.getKey().compareTo(o.getKey()) ;
}
}
//前序遍历
public void preOrder() {
preOrder(root);
}
//前序遍历-递归方式 以node为根节点 前序遍历DLR
private void preOrder(Node node) {
if (node == null) {
return;
}
System.out.println(node.key);
preOrder(node.left);
preOrder(node.right);
}
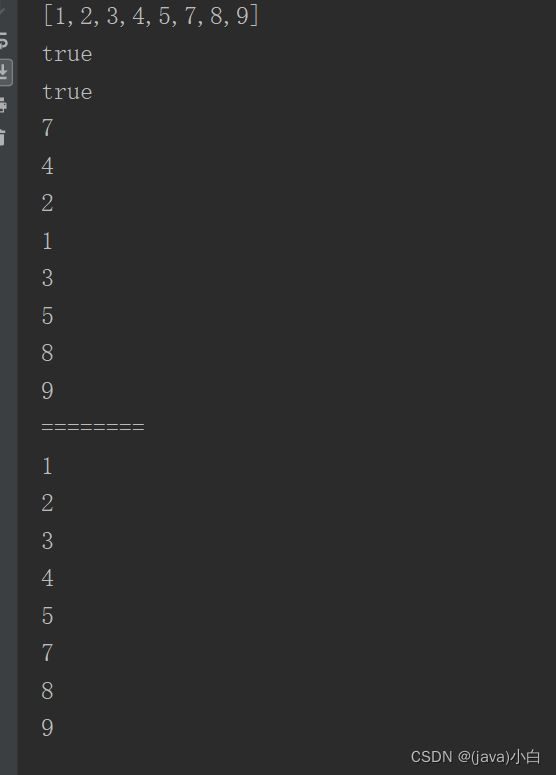
} 测试代码
public class TestAVLTreeMap {
public static void main(String[] args) {
AVLTM map = new AVLTM<>();
map.put(6, "666");
map.put(4, "444");
map.put(3, "333");
map.put(7, "777");
map.put(5, "555");
map.put(9, "999");
map.put(8, "888");
map.put(1, "111");
map.put(2, "222");
map.remove(6);
System.out.println(map.keySet());
System.out.println(map.isBST());
System.out.println(map.isBalanced());
map.preOrder();
System.out.println("========");
map.inOrder(); 运行结果