Python3.WRF的投影转换

有一种WRF输出的数据采用兰伯特双标准纬线投影，那么除非刚好需要同样的投影，想对这种数据进行处理的话往往要进行投影转换，WRF应该是有一套工具可以进行相关的处理，比如wrf-python，但是作为并不熟悉wrf、仅仅是使用WRF输出数据的小白，去使用WRF系工具的话学习成本就比较高了，如何用熟悉、更通用的工具实现这一投影转换呢？

难道不是设置几个投影参数，用常见的投影相关的包就可以实现了吗？

对，问题在于这个参数怎么设置？这个坑还是很坑的，好在最终找到一篇2018年的英文博客https://fabienmaussion.info/2018/01/06/wrf-projection/，加上我自己的尝试和理解，梳理出本文

采用WRF输出的数据格式为GrADS二进制码

关键

从我的角度来看，WRF的兰伯特双标准纬线投影有两个坑：

1. 椭球体参数
2. 投影中心参数

完全不了解WRF输出的情况下

“啪”的一下，很快啊，观察到WRF输出的GrADS二进制数据对应的ctl文件中pdef如下所示

pdef  288 288 lcc  32.318  117.203  144.500  144.500  60.00000  30.00000  117.30000   3000.000   3000.000

然后查到pdef的lcc语法如下：

那么熟悉GDAL的小伙伴应该就会很开心地想：哟，这不就是SetLCC里需要的参数吗？咱这么写（默认WGS84地理坐标系）：

from osgeo import osr

(isize, jsize, latref, lonref, iref, jref, Struelat, Ntruelat, slon, dx, dy) = \
    (288, 288, 32.318, 117.203, 144.5, 144.5, 60, 30, 117.3, 3000, 3000)

lcc = osr.SpatialReference()
lcc.SetLCC(Struelat, Ntruelat, latref, lonref, iref * dx, jref * dy)
lcc.SetLinearUnitsAndUpdateParameters('kilometre', 3000)
geo = lcc.CloneGeogCS()
geo2lcc = osr.CoordinateTransformation(geo, lcc)
lcc2geo = osr.CoordinateTransformation(lcc, geo)

接下来通过geo2lcc和lcc2geo就可以愉快的在投影坐标和地理坐标之间反复横跳了不是？

当然我们需要验证。WRF输出数据中有XLAT和 XLONG两个要素，描述每个格点对应的经纬度（即地理坐标），加上很自然认为投影坐标是均匀地从西南角(0, 0)到东北角(isize-1, jsize-1)，如果能够用我们的lcc2geo计算出的经纬度矩阵与XLAT和 XLONG一致那就说明可以放心地左右横跳

x = np.arange(isize)
y = np.arange(jsize)
x_mesh, y_mesh = np.meshgrid(x, y)
latlon = np.array(lcc2geo.TransformPoints(np.vstack([x_mesh.ravel(), y_mesh.ravel()]).T))
lat = latlon[:, 0].reshape(shape)
lon = latlon[:, 1].reshape(shape)

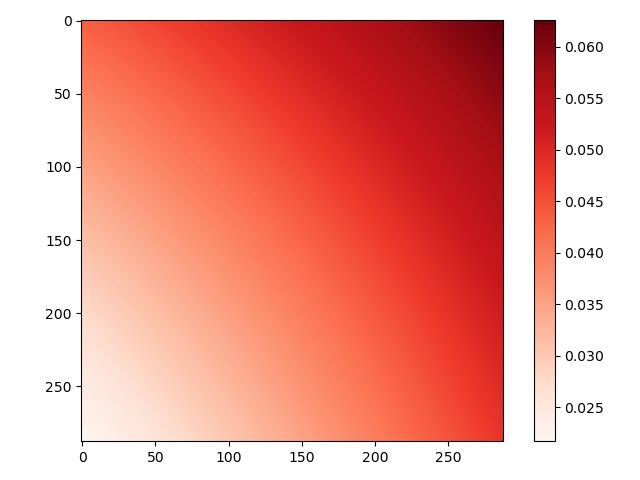
然而当我们计算出咱们的经纬度坐标lat和lon后，与XLAT和 XLONG作差（欧氏距离）快速画个图一看：

d = ((lat - lat_in_wrf)**2 + (lon - lon_in_wrf)**2)**0.5

import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
im = ax.imshow(d, cmap='Reds')
cb = fig.colorbar(im, ax=ax)
fig.set_tight_layout(True)

这时候就有弹幕说：“我不满意！”其实我也不满意，误差有点大，但是也没大到离谱，说明应该是投影参数有一点点问题。

修正椭球体参数

于是查资料发现，WRF的椭球体不是椭球体，是【芬芳的语气词】一个半径为6370000米的正球体！那么咱这么干：

lcc = osr.SpatialReference()
lcc.ImportFromProj4('+proj=longlat +a=6370000 +b=6370000 +no_defs')
lcc.SetLCC(Struelat, Ntruelat, latref, lonref, iref * dx, jref * dy)
lcc.SetLinearUnitsAndUpdateParameters('kilometre', 3000)
geo = lcc.CloneGeogCS()
geo2lcc = osr.CoordinateTransformation(geo, lcc)
lcc2geo = osr.CoordinateTransformation(lcc, geo)

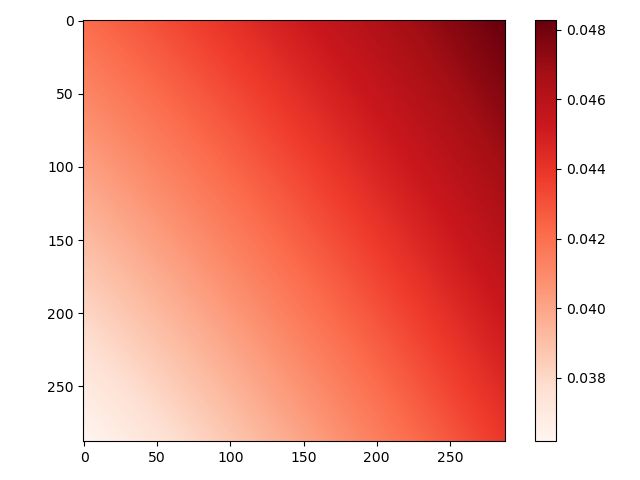
再画个图瞧瞧

【芬芳的语气词】！但是可以发现最大误差变小了，说明有所改进，最小误差变大了，说明剩下的误差应该是水平偏移的成分多一些了。

继续查资料

修正投影中心地理坐标参数并计算投影坐标

终于，找到开头提到的博客。我虽然不会WRF，但是根据我的理解：WRF大概有两个区域，大区域里嵌套小区域，投影参数是按大区域的来，最终产出的数据是小区域的。这意味着，pdef中的latref和lonref并不是投影中心地理坐标，只是一个reference（洋屁，“参考”的意思），是用来计算真正的投影坐标用的，而真正的投影中心地理坐标，是MOAD_CEN_LAT和STAND_LON，在ctl文件中最下面像注释一样的东西里

@ global String comment MOAD_CEN_LAT =        32.40
@ global String comment STAND_LON =       117.30

那么咱这么干：

MOAD_CEN_LAT = 32.40
STAND_LON = 117.30

lcc = osr.SpatialReference()
lcc.ImportFromProj4('+proj=longlat +a=6370000 +b=6370000 +no_defs')
lcc.SetLCC(Struelat, Ntruelat, MOAD_CEN_LAT, STAND_LON, 0, 0)
lcc.SetLinearUnitsAndUpdateParameters('kilometre', 3000)
geo = lcc.CloneGeogCS()
geo2lcc = osr.CoordinateTransformation(geo, lcc)
lcc2geo = osr.CoordinateTransformation(lcc, geo)

e, n, _ = geo2lcc.TransformPoint(lonref, latref)
false_west = -(iref-1) + e
false_south = -(jref-1) + n
x, y = np.arange(isize) + false_west, np.arange(jsize) + false_south
x_mesh, y_mesh = np.meshgrid(x, y)

lonlat = np.array(lcc2geo.TransformPoints(np.vstack([x_mesh.ravel(), y_mesh.ravel()]).T))
lon = lonlat[:, 0].reshape(shape)
lat = lonlat[:, 1].reshape(shape)

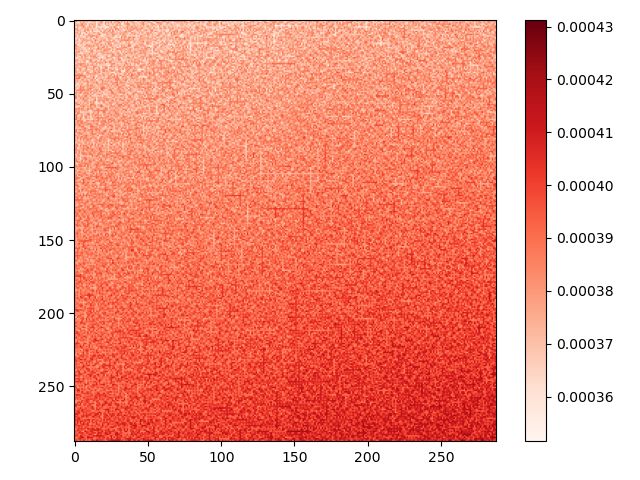
再画个图瞧瞧

误差降了两个数量级啦，我已经比较满意了

---

总结一下

• WRF投影中心参数为MOAD_CEN_LAT和STAND_LON，采用的椭球体为半径为6370000米的正球体
• pdef中的latref和lonref表示输出数据第jref行第iref列的地理坐标（经纬度），不代表投影中心（jref和iref是从1开始计数的）

讨论一下

• 我觉得投影坐标的绝对数值由于直接受单位和偏移的影响可以任意变化，真正反映出空间信息的是投影坐标之间的差值（相对数值），所以我在最后的SetLCC投影参数中没有设置false_east和false_north偏移（最后两个参数）。虽然可以求出符合WRF输出数据的false_east和false_north，再调用一次lcc.SetLCC获得“完美投影关系”，但是似乎会让人感到更复杂。（其实作为非地理专业的我，这段话就已经有点绕了，权当作讨论再绕一点：最后一段代码中lcc.SetLinearUnits也是没有必要的，之后所有距离按米计算就行）
• 原文采用pyproj进行投影，由于我更熟悉GDAL所以换成了GDAL实现。但是吐槽一点，TransformPoint这个方法在公开地理坐标系下如WGS84传参或返回的地理坐标都是先纬度再经度（如本文第一次调用），在自定义地理坐标系下传参或返回的地理坐标却是先经度再维度（本文最后两次调用），这也有可能是我用得不好，有了解的读者麻烦指教一下
• 原文的WRF输出是nc，我用的WRF输出是GrADS二进制码，不影响这个投影的逻辑
• 原文误差在10^-5，而本文误差在10^-4，我觉得应该是nc文件提供的各参数小数位数比GrADS的ctl文件多
• 查资料时发现WRF也有基于WGS84的数据，不在本文讨论范围内