运筹说 第53期 | 智能优化算法介绍之粒子群算法

本期为大家带来的是运筹学智能优化算法——粒子群算法（PSO）的讲解。我们将简单介绍一下粒子群算法的产生背景和基本思想，并重点介绍实现粒子群算法求解实际问题的Python及MATLAB相关代码，以帮助大家更好的理解和运用粒子群算法。话不多说，我们一起来看看吧！

 

1、算法介绍

1.1、产生背景

自然界中的鸟群和鱼群的群体行为一直是科学家的研究兴趣所在。1990年，生物学家 Frank Heppner 提出了鸟群聚集模型，在他的仿真中，一开始每一只鸟都没有特定的飞行目标，只是使用简单的规则确定自己的飞行方向和飞行速度，当有一只鸟飞到栖息地附近时，它周围的鸟也会跟着飞向栖息地，最终整个鸟群都会落在栖息地。利用上面几条简单的规则，就可以非常接近地模拟出鸟群飞行的现象。l995年，美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出了粒子群算法（James Kennedy社会心理学家。自1994年起，他一直致力于粒子群算法的研究工作，目前在美国劳工部从事调查方法的研究工作。他在计算机科学和社会科学杂志和学报上发表过许多关于粒子群的论文。RusselI C．Eberhart　美国印第安纳州普度大学电子与计算机工程系主任，IEEE会士，曾任IEEE神经网络委员会的主席，著有《计算智能：从概念到实现》等）。

该算法的提出是受对鸟类群体行为进行建模与仿真的研究结果的启发。他们的模型和仿真算法主要对Frank Heppner的模型进行了修正，以使粒子飞向解空间并在最优解处降落。它模拟鸟类的觅食行为，将求解问题的搜索空间比作鸟类的飞行空间，将每只鸟抽象成一个没有质量和体积的粒子，用它来表征问题的一个可能解，将寻找问题最优解的过程看成鸟类寻找食物的过程，进而求解复杂的优化问题。

粒子群算法具有很好的生物社会背景而易于理解，由于参数少而容易实现，对非线性、多峰问题均具有较强的全局搜索能力，已广泛应用于函数优化、神经网络训练、模式分类、模糊控制等领域。

1.2、基本思想

在粒子群算法中，潜在解的改进是合作的结果，而在进化算法中则是因为竞争。这个概念使得群体智能有别于进化算法。简而言之，在进化算法中，每一次迭代都有一个新的种群进化，而在群智能算法中，每一代都有个体使自己变得更好。通过将群体中的个体看作在D维搜索空间中没有质量和体积的粒子，每个粒子以一定的速度在解空间运动，并向自身历史最佳位置pbest和邻域历史最佳位置gbest聚集，实现对候选解的进化。通俗来讲，思路如下：
★1.每只鸟（粒子）随机在一个位置搜索，评估这个地方的食物量。
★2.所有的鸟信息共享，选出当前这群鸟遇到的食物量最多的位置作为飞行目标的候选点g。
★3.每只鸟回顾自己的旅程，记住自己曾经去过的食物量最多的位置p。
★4.每只鸟为了找到食物量更多的位置，于是向着g点飞行，但是考虑鸟儿飞行的惯性，也就是鸟儿无法从p和g点进行选择，由于惯性它会下一次飞行到达位置q 。
★5.如果小鸟们决定停止寻找，那么它们会选择当前的g点；否则继续上述步骤来寻找它们的栖息地。

现在我们赋予鸟儿一些参数：

· N：群落中的粒子个数，i＝1，2，...，N
· D：搜索空间的维度，j＝1，2，...，D
· C1：个体学习因子，也称为个体加速因子。这个因子越大，鸟儿越倾向于飞往它自己曾去的食物量最多的地方。
· C2：社会学系因子，也成为社会加速因子。这个因子越大，鸟儿越倾向于飞往其他鸟儿（同伴们）曾去的食物量最多的地方。
· r1、r2：[0,1]上的随机数。随机代表着鸟儿比较佛系，他也不知道飞哪里。
· w：惯性权重，也叫惯性系数，这个数越大，代表着它不容易更改之前的运动路线，更倾向于探索未知领域。

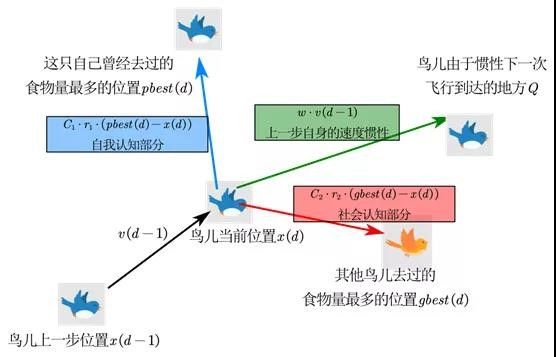
根据以上参数，速度和位置更新公式为：

 式（1）中，第一部分表示粒子先前的速度，用于保证算法的全局收敛性能；第二部分、第三部分则使算法具有局部收敛能力。惯性权重w表示在多大程度上保留原来的速度：w较大，则全局收敛能力较强，局部收敛能力较弱；w较小，则局部收敛能力较强，全局收敛能力较弱。示意图如下：

2、应用案例

2.1、案例分析

问题描述（TSP问题）：

假设有一个旅行商人要拜访全国31个省会城市，全国31个省会城市的坐标已给出，他需要选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。并且要求所选路径的总路程为所有路径之中的最小值。

粒子群算法过程：

（1）初始化群体粒子个数N，粒子维数D,最大迭代次数T，学习因子c1、c2,惯性权重最大值Wmax，惯性权重最小值Wmin。

（2）初始化速度v和种群粒子位置x，计算个体适应度值，获得粒子个体最优位置p和最优值pbest，以及粒子群全局最优位置g和最优值gbest。

（3）根据权重值w,更新速度值v，进行边界条件处理判断，并更新位置x，计算适应度值，判断是否替换粒子个体最优位置p和最优值pbest，以及粒子群全局最优位置g和最优值gbest。

（4）判断是否满足终止条件：如果满足则结束搜索过程，输出优化值；如果不满足，则继续进行迭代。

2.2、代码实现

基于以上求解步骤及思想，借助MATLAB和Python两种平台分别实现粒子群算法求解TSP问题的详细代码以及最终的运行结果。由于篇幅有限，部分代码如下（感兴趣的小伙伴们关注“运筹学”公众号后台回复“粒子群算法MATLAB”及“粒子群算法Python”即可获取完整代码）

（1）MATLAB

★代码展示

MATLAB平台实现求解PSO算法需要分别建立一个主函数文件和若干函数，本案例群体的粒子数为500，每个粒子的维数为31，算法迭代进化次数为200。加速度因子c1=0.5，c2=0.7，惯性权重w=0.96。生成随机初始解的部分代码如代码1所示，适应度函数的计算即路径距离的部分代码如代码2所示。标准粒子群算法中速度位置的更新是直接采用加权的方式进行，但是对于求解TSP问题难以直接套用。所以常见的做法是引用交换子和交换序进行求解，也就是pij-xij 为粒子与个体极值的交换序,pgj-xij为粒子与全局极值的交换序，并以c1，c2的概率保留，之后更新各路径总距离。部分代码如代码3所示。产生交叉算子和保留的过程由单独的函数文件GenerateChangeNums、HoldByOdds计算。小伙伴们可以关注“运筹学”公众号→后台回复“粒子群算法MATLAB代码”获取完整代码。

★代码调用及运行结果

案例求解的最终结果和示意图如下，途经31个城市的最短路径距离为16399。可以看出和初始解相比，优化后的路径方案更加合理，并且在进化收敛速度方面性能较好。

（2）Python

★代码展示

求解流程与上述步骤相同，程序的运行逻辑也基本一致。计算城市之间的距离和评价函数的部分代码如代码1所示，在这里引入了遗传算法的轮盘赌的思想产生交叉算子，即采用混合型粒子群算法进行求解，对惯性因子w、自我认知因子c1、社会认知因子c2分别以

的概率接受粒子本身逆序、当前最优解、全局最优解作为子代。

由于篇幅有限，小伙伴们可以关注“运筹学”公众号→后台回复“粒子群算法Python”获取完整代码。

★代码调用及运行结果
点击运行，得到最短距离为15450。可以看出由于交叉序的设计不同，使用第二种方法运行求解得到的结果相对更优。

☆ 参考资料：

《人工智能导论》

【粒子群算法】：
https://blog.csdn.net/daaikuaichuan/article/details/81382794
【粒子群算法matlab实现】：
粒子群算法及MATLAB代码仿真实例 - 知乎
公众号：python学习杂记：Python粒子群算法实现、数学建模：非常通俗易懂的粒子群算法（PSO）入门

本期的内容就介绍到这里，想要进一步了解运筹算法，关注本公众号，快快学起来吧！

回复“粒子群算法MATLAB”获得代码！

运筹说

作者 | 陈楠

责编 | 刘文志

审核 | 徐小峰