Codeforces Round #833 (Div. 2)

A. The Ultimate Square

答案是n/2上取整。

B. Diverse Substrings

由于是数字串，容易发现满足条件的子串最长是100（鸽巢原理），故暴力即可

C. Zero-Sum Prefixes

前缀和数组，考虑贪心。假设从原数组第一个0的位置到最后，可以吧数组分成k个子区间，答案等于每个子区间对应的前缀和数组中出现次数最多次数之和。
AC代码：

#include 

using namespace std;
typedef long long ll;
#define int ll
#define endl '\n'
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

const int maxn = 2e5 + 5;
int t, n, ans;
int ar[maxn];
map<int, int> mp;
vector<int> vt;

signed main()
{
    //io;
    cin >> t;
    while(t--)
    {
        cin >> n;
        vt.clear();
        ans = 0;
        for(int i = 1; i <= n; ++i)
        {
            cin >> ar[i];
            if(ar[i] == 0) vt.push_back(i);
            ar[i] += ar[i - 1];
        }

        int l, r, mx;
        for(int i = 0; i < vt.size(); ++i)
        {
            l = vt[i];
            if(i != vt.size() - 1) r = vt[i + 1] - 1;
            else r = n;
            mp.clear();
            mx = 0;
            for(int j = l; j <= r; ++j) mx = max(mx, ++mp[ar[j]]);
            ans += mx;
        }
        if(vt.size())
        {
            for(int i = 1; i < vt[0]; ++i)
                if(ar[i] == 0) ++ans;
        }
        else
        {
            for(int i = 1; i <= n; ++i)
                if(ar[i] == 0) ++ans;
        }
        cout << ans << '\n';
    }

    return 0;
}

D. ConstructOR

题意：
给你a，b，d，让你找一个x，满足$a|x$能整除$d$，$b|x$能整除$d$,$(1<=a,b,d<=2^{30},0<=x<=2^{60})$。
分析：
假设$aa$是第一个大于$a|b$的2的n次幂，容易想到方程$aa\ast x+a|b=d\ast y$,解出一个正的x，答案就是$aa\ast x+a|b$，方程无解，就是-1，（答案可以取到$2^{60}$，故可以考虑这样子）。
AC代码：

#include 

using namespace std;
#define int long long
#define endl '\n'
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;

const int maxn = 2e5 + 5;
int n, m, k, x;
int aa, bb, dd;
int t;

ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if(b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    ll r = exgcd(b, a % b, x, y);
    ll t = x;
    x = y;
    y = t - a / b * y;
    return r;
}

signed main()
{
    //io;
    cin >> t;
    int a, b, c, d;
    int x0, y0, x1, y1;
    int dx, dy;
    while(t--)
    {
        cin >> aa >> bb >> dd;
        c = (aa|bb);
        int bas = 1;
        for(int i = 1; i <= 60; ++i)
        {
            bas = bas * 2ll;
            if(bas > c)
            {
                a = bas;
                break;
            }
        }
        c = -c;
        b = -dd;

        d = exgcd(a, b, x0, y0);
        if((c % d) != 0)
        {
            cout << -1 << '\n';
            continue;
        }

        x1 = x0 * c / d;
        dx = abs(b / d);
        x1 = (x1 % dx + dx) % dx;
        int ans = bas * x1 + (aa|bb);
        cout << ans << '\n';
    }
    return 0;
}

E. Yet Another Array Counting Problem

题意：
给你一个长度为n的数组ar[i],子区间[l,r]的权值等于数字x=max(ar[l],ar[l+1],...,ar[r])在区间中第一次出现的位置（最靠左的位置）pos,让你找一个长度为n的数组br，满足1<=br[i]<=m，并且所有n*(n+1)/2个子区间的权值相同。
分析：
构造原数组的笛卡尔树，可以发现对于一个区间[l,r],它的权值就是节点l,l+1,...,r的LCA。数组br只需要有和它一样的笛卡尔树即可。故作树形dp,定义为dp[n][m],注意到n的取值虽然达到2e5，但是n*m只有1e6,故n*m的dp是行得通的，加之前缀和优化一下即可实现$O(1)$转移，总体复杂度O(n*m)

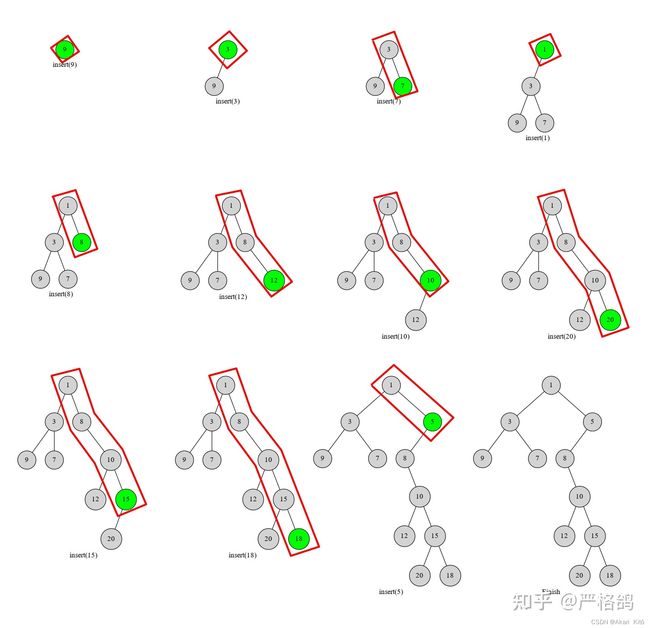
（图片来源：知乎ygg）
AC代码：

#include 

using namespace std;
#define int long long
#define endl '\n'
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
typedef long long ll;

const int maxn = 2e5 + 5;
const int mod = 1e9 + 7;
struct node
{
    int l, r;
} tree[maxn];
int t, n, m;
int top, k, root;
int ar[maxn];
int stk[maxn];

int build()
{
    top = 0;
    for(int i = 1; i <= n; ++i)
    {
        k = top;
        while(k && ar[stk[k]] < ar[i]) --k;
        if(k) tree[stk[k]].r = i;
        if(k < top) tree[i].l = stk[k + 1];
        stk[++k] = i;
        top = k;
    }
    return stk[1];
}

void work()
{
    cin >> n >> m;
    for(int i = 1; i <= n; ++i) cin >> ar[i];
    for(int i = 1; i <= n; ++i) tree[i].l = tree[i].r = 0;

    root = build();
    vector<vector<int>> dp(n + 1, vector<int>(m + 1));
    for(int i = 0; i <= m; ++i) dp[0][i] = 1;

    function<void(int)> dfs = [&](int u)
    {
        if(tree[u].l) dfs(tree[u].l);
        if(tree[u].r) dfs(tree[u].r);

        for(int i = 1; i <= m; ++i)
        {
            dp[u][i] = (dp[tree[u].l][i - 1] * dp[tree[u].r][i]) % mod;
            dp[u][i] = (dp[u][i] + dp[u][i - 1]) % mod;
        }
    };

    dfs(root);
    cout << dp[root][m] << '\n';
}

signed main()
{
    io;
    cin >> t;
    while(t--) work();
    return 0;
}