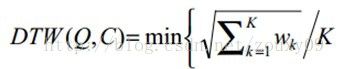DTW+matlab之辣鸡学算法
为了无愧于良心,决定标注为转载+整理,毕竟我也没什么个人见解,纯粹整理网上广为流传的内容并尽力理解而已。
首先附上转载的网站
1Dynamic Time Warping 动态时间规整算法
2DTW的原理及matlab实现(转载+整理)
3HMM学习笔记_1(从一个实例中学习DTW算法)
4【重大修改】动态时间规整(Dynamic Time Warping)
1的评论区里似乎有大佬改进的代码
2比较全面的整合了DTW的原理和来自3的实例
123的代码相似,而4则提出了一个新的代码,否了123所用代码,表述为可视化DTW,代码段超长/(ㄒoㄒ)/~~
here we go!
DTW算法原理和代码整理
- 原理
-
- 时间序列数据
- DTW算法
-
- 概述
- 思路
- 具体步骤
- 实例
-
- 实例1
- 实例2
- 代码
-
- 代码1
-
- dtw.m
- main.m
- 代码2
-
- dtw.m
- test.m
原理
时间序列数据
首先了解一下DTW作用于的数据,时间序列数据,比较两个时间序列数据的相似性是一种普遍的研究方式。
在时间序列中,需要比较相似性的两段时间序列的长度可能并不相等,在语音识别领域表现为不同人的语速不同。因为语音信号具有相当大的随机性,即使同一个人在同时刻发同一个音,也不可能具有完全的时间长度。而且同一个单词内的不同音节的发音速度也不同,比如有的人会把“A”这个音拖得很长,或者把“i”发的很短。
由此,会产生信号相似,但时间上不太对齐的现象,所以,使用传统的欧几里得距离无法有效地求出两个时间序列之间的距离(或者相似性)。
例如图A所示,实线和虚线分别是同一个词“pen”的两个语音波形(在y轴上拉开了,以便观察)。可以看到他们整体上的波形形状很相似,但在时间轴上却是不对齐的。例如在第20个时间点的时候,实线波形的a点会对应于虚线波形的b’点,这样传统的通过比较距离来计算相似性很明显不靠谱。因为很明显,实线的a点对应虚线的b点才是正确的。 而在图B中,DTW就可以通过找这两个波形对齐的点计算它们之间距离。
由B)图可以看出,模板序列中的一个点(这里的点可能是单个数值或是一个向量)可能对应测试序列中的好几个点(也有可能反过来,模板中的好几个点对应测试中的一个点),这正好反映了特征可能的延迟性。比如同一个音节,有的时候发得快,有的时候发的慢。这两种情况进行匹配时,你要把发得快的那个点完全匹配到发的慢的那几个点上。
当两个序列整体上具有非常相似的形状,但是这些形状在x轴上并不是对齐时。我们要在比较他们的相似度之前,将其中一个(或者两个)序列在时间轴下warping扭曲,以达到更好的对齐。而DTW就是实现这种warping扭曲的一种有效方法。DTW通过把时间序列进行拉长和缩短,来计算两个时间序列性之间的相似性。
DTW算法
概述
DTW(Dynamic Time Warping )动态时间规整算法,是一种衡量两个时间序列之间的相似度的方法,把两个代表同一个类型的事物(如同一个单词发音或动作)的不同长度序列进行时间上的“对齐”(用一个函数拉长或者缩短其中一个信号,这样warping一个序列后可以与另一个序列重合,此时两个序列中所有对应点的距离之和最小,同时它们之间的误差也达到最小。)。主要应用在语音识别领域来识别两段语音是否表示同一个单词。
就像使用神经网络进行训练一样,做DTW都事先需要一个对照组一个测试组。对照组已经识别出了该时间序列数据的标签,而测试组待识别的时间序列长度又和对照组不同,怎么办呢?
我们可以让已标签时间序列的每一帧找到无标签的时间序列的对应帧,使得它们的距离最短。这样便可以计算出两个时间序列的相似度,然后设定一个阈值,满足阈值范围就把未知时间序列加上某标签。
动态时间规整DTW是一个典型的优化问题,它用满足一定条件的时间规整函数W(n)描述测试组和对照组的时间对应关系,求解两组时间序列匹配时累计距离最小所对应的规整函数。
思路
假设我们有两个时间序列Q和C,他们的长度分别是n和m:(实际语音匹配运用中,一个序列为对照组,一个序列为测试组,序列中的每个点的值为语音序列中每一帧的特征值。例如语音序列Q共有n帧,第i帧的特征值(一个数或者一个向量)是qi。至于取什么特征,在这里不影响DTW的讨论。我们需要的是匹配这两个语音序列的相似性,以识别我们的测试语音是哪个词)
Q = q1, q2,…,qi,…, qn ;
C = c1, c2,…, cj,…, cm ;
如果n=m,那么就用不着折腾了,直接计算两个序列的距离就好了。但如果n≠m我们就需要对齐。
最简单的对齐方式就是线性缩放。 把短的序列线性放大到和长序列一样的长度再比较,或者把长的线性缩短到和短序列一样的长度再比较。但是这样的计算没有考虑到语音中各个段在不同情况下的持续时间会产生或长或短的变化,因此识别效果不可能最佳。比如原本一个词说的很快,硬拉长后会导致语音模糊,在某一段内与对照组对比会出现很多对应点,听哪几秒都像在说一个音,无法实现准确识别。
因此更多的是采用动态规划(dynamic programming)的方法。
为了对齐这两个序列,我们需要构造一个n x m的矩阵网格,矩阵元素(i, j)表示qi和cj两个点的距离d(qi, cj)(也就是序列Q的每一个点和C的每一个点之间的相似度,距离越小则相似度越高),一般采用欧式距离,d(qi, cj)= (qi-cj)²(也可以理解为失真度)。每一个矩阵元素(i, j)表示点qi和cj的对齐。最终寻找一条通过此网格中若干格点的路径,路径通过的格点即为两个序列进行计算的对齐的点。

那么这条路径我们怎么找到呢?哪条路径才是最好的呢?也就是刚才那个问题,怎么样的warping才是最好的。
两个序列长度不同时,不能使用欧氏距离进行匹配。DTW以DP算法为理念,使用DTW,上图方格中的每个连续的点(保证开头(1,1)和结尾(m,n))构成的曲线都有可能,而我们能需要找出代价最小的那条曲线,如图中标出的黑色曲线。
我们把最终的路径定义为warping path规整路径,并用W来表示, W的第k个元素定义为wk=(i,j)k,定义了序列Q和C的映射。
这样我们有:
首先,这条路径不是随意选择的,需要满足以下几个约束:
- 边界条件:w1=(1, 1)和wK=(m, n)。任何一种语音的发音快慢都有可能变化,但是其各部分的先后次序不可能改变,因此所选的路径必定是从左下角出发,在右上角结束。
- 连续性:如果wk-1= (a’, b’),那么对于路径的下一个点wk=(a, b)需要满足 (a-a’) <=1和 (b-b’) <=1。也就是不可能跨过某个点去匹配,只能和自己相邻的点对齐。这样可以保证Q和C中的每个坐标都在W中出现。
- 单调性:如果wk-1= (a’, b’),那么对于路径的下一个点wk=(a, b)需要满足0<=(a-a’)和0<= (b-b’)。这限制W上面的点必须是随着时间单调进行的。以保证图B中的虚线不会相交。
结合连续性和单调性约束,每一个格点的路径就只有三个方向了。例如如果路径已经通过了格点(i, j),那么下一个通过的格点只可能是下列三种情况之一:(i+1, j),(i, j+1)或者(i+1, j+1)。

满足上面这些约束条件的路径可以有指数个,然后我们要得到的是使得下面的规整代价最小的路径:
分母中的K主要是用来对不同的长度的规整路径做补偿。
我们的目的是什么?或者说DTW的思想是什么?是把两个时间序列进行延伸和缩短,来得到两个时间序列距离最短也就是最相似的那一个warping,这个最短的距离也就是这两个时间序列的最后的距离度量。在这里,我们要做的就是选择一个路径,使得最后得到的总的距离最小。
这里我们定义一个累加距离cumulative distances。从(0, 0)点开始匹配这两个序列Q和C,每到一个点,之前所有的点计算的距离都会累加。到达终点(m,n)后,这个累加距离就是我们上面说的最后的总的距离,也就是序列Q和C的相似度。
累加距离γ(i,j)可以按下面的方式表示:累加距离γ(i,j)为当前格点距离d(i,j),也就是点qi和cj的欧式距离(相似性)与可以到达该点的最小的邻近元素的累加距离之和:
注明:先把对照组和测试组的每个点相对应的距离算出来,构成一个mxn的矩阵。然后根据每个元素的代价计算一条最短路径。这里的计算要符合以上三个约束。即,一个点的代价=这个点的值+来自min{下、左、斜下这三个方向的值}。所以可知该算法使用逆推导的形式,每个点的下、左、斜下这三个方向的值可以依次递归求得,从终点(m,n)开始,直到(1,1)点结束。
具体步骤
- 首先,已知存在两个或多个序列,但比较时必须两两进行,所以假设有两个序列,A={a1,a2…am},B={b1,b2…bn},其中每个分量可以是一个数或者是一个更小的向量,在这里设总维数m>n。注意M不一定等于N,但是每个分量的维数应该相同。
- 然后,用欧氏距离计算出两序列的每两点之间的距离,D(ai,aj),其中1≤i≤m,1≤j≤n
画出下表:
-
根据上图找出最短路径。从D(a1,b1)沿着某条路径到达D(am,bn)。找路径满足:假如当前节点是D(ai,bj),那么下一个节点必须是在D(i+1,j),D(i,j+1),D(i+1,j+1)之间选择,并且路径必须是最短的。计算的时候是按照动态规划的思想计算,也就是说在计算到达第(i,j)个节点的最短路径时候,考虑的是左上角也即第(i-1,j)、(i-1,j-1)、(i,j-1)这三个点到(i,j)的最短距离。
-
接下来从最终的最短距离往回找到那条最佳的输出路径, 从D(a1,b1)到D(am,bn)。他们的总和就是就是所需要的DTW距离。
【注】如果不回溯路径,直接在第3步的时候将左上角三个节点到下一个节点最短的点作为最优路径节点,就是贪婪算法了。DTW是先计算起点到终点的最小值,然后从这个最小值回溯回去看看这个最小值都经过了哪些节点。
实例
实例1
已知:两个列向量a=[8 9 1]’,b=[ 2 5 4 6]’,其中’代表转置,也就是把行向量转换为列向量
求:两个向量利用动态时间规整以后的最短距离
第一步:计算对应点的欧式距离矩阵d【注意开根号】
6 3 4 2
7 4 5 3
1 4 3 5
第二步:计算累加距离D【从6出发到达5的累加距离】
(D(i,j)是从上往下数的第一行第一列)
把(1,1)往上的部分当作0。所以对于下一个点,其上一个格点的情况为

6 9 13 15
13 10 14 16
14 14 13 18
计算方法如下:
D(1,1)=d(1,1)=6
D(1,2)=D(1,1)+d(1,2)=9
…
D(2,2)=min(D(1,2),D(1,1),D(2,1))+d(2,2)=6+4=10
…
D(m,n)=min(D(m-1,n),D(m-1,n-1),D(m,n-1))+d(m,n)
注:在该实例中,使用从下往上的计算方法无法得到如上的最终距离,18。只得到了11。也就证明算错了,具体原因见实例2中的区别分析。
实例2
就是转载网页3的内容
相比实例1,实例2引用的更广泛,而且说明更详细,包括了记录路径并往回推导。唯一有争议的点就是斜向距离是否必须×2。如果结合实例1看,斜向距离只需要×大于等于1的值。
而且我认为实例1和2的区别在于:对比两个原始数据时,放置的方位不同,导致初始判定为0的位置不同,所以整体距离趋向方向不同,对于下一个点,其上一个格点的情况也不同。
假设现在有一个标准的参考模板R,是一个M维的向量
R={R(1),R(2),……,R(m),……,R(M)},每个分量可以是一个数或者是一个更小的向量。
现在有一个才测试的模板T,是一个N维向量
T={T(1),T(2),……,T(n),……,T(N)},同样每个分量可以是一个数或者是一个更小的向量,注意M不一定等于N,但是每个分量的维数应该相同。
由于M不一定等于N,计算R和T的相似度的时候选用DTW算法。
首先我们应该知道R中的一个分量R(m)和T中的一个分量T(n)的维数是相同的,它们之间可以计算相似度(即距离)。在运用DTW前,我们要首先计算R的每一个分量和T中的每一个分量之间的距离,形成一个M*N的矩阵。(为了方便,行数用将标准模板的维数M,列数为待测模板的维数N)。
然后下面的步骤该怎么计算呢?用个例子来看看。
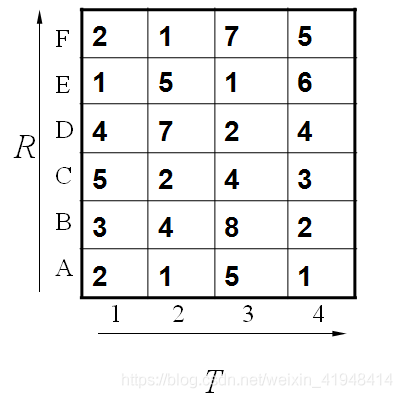
这个例子中假设标准模板R为字母ABCDEF(6个),测试模板T为1234(4个)。R和T中各元素之间的距离已经给出(提前假设的欧式距离)。如下:
既然是模板匹配,所以各分量的先后匹配顺序已经确定了,虽然不是一一对应的。我们的目的是要计算出测试模板T和标准模板R之间的距离。因为2个模板的长度不同,所以其对应匹配的关系有很多种,我们需要找出其中距离最短的那条匹配路径。
现假设题目满足如下的约束:当从一个方格((i-1,j-1)或者(i-1,j)或者(i,j-1))中到下一个方格(i,j),如果是横着或者竖着的话其距离为d(i,j),如果是斜着对角线过来的则是2d(i,j).
其约束条件如下图像所示:
其中g(i,j)表示两个模板都从起始分量逐次匹配,已经到了M中的i分量和T中的j分量,表示两个模板之间的距离。并且都是在前一次匹配的结果上加d(i,j)或者2d(i,j),然后取最小值。
所以我们将所有的匹配步骤标注后如下:
怎么得来的呢?
比如说g(1,1)=4
当然前提都假设是g(0,0)=0,就是说g(1,1)=g(0,0)+2d(1,1)=0+2*2=4.
g(2,2)=9是一样的道理。
如果从g(1,2)来算的话是g(2,2)=g(1,2)+d(2,2)=5+4=9,因为是竖着上去的。
如果从g(2,1)来算的话是g(2,2)=g(2,1)+d(2,2)=7+4=11,因为是横着往右走的。
如果从g(1,1)来算的话,g(2,2)=g(1,1)+2d(2,2)=4+24=12.因为是斜着过去的。
综上所述,取最小值为9. 所有g(2,2)=9.
当然在这之前要计算出g(1,1),g(2,1),g(1,2)。因此计算g(i,j)也是有一定顺序的。
其基本顺序可以体现在如下:
计算了第一排,其中每一个红色的箭头表示最小值来源的那个方向。当计算了第二排后的结果如下:
最后都算完了的结果如下:
到此为止,我们已经得到了答案,即2个模板直接的距离为26。 我们还可以通过回溯找到最短距离的路径,通过箭头方向反推回去。如下所示:

楼主讲了:这里横竖项加d(i,j)以及斜向加2×d(i,j)只是为了举个例子,没什么依据的,你也可以斜向加n×d(i,j),只需取n>1即可。d(i,j)的含义是在这个例子中只是一个模版匹配路径的单位消耗代价,这里取的是1。那个最后算出来的距离26也只是一个相对的概念。
但据实例1了解,n也可以等于1。
代码
代码1
在转载网页1的评论区中
dtw.m
function dist = dtw(t,r)
n = size(t,1);
m = size(r,1);
% 帧匹配距离矩阵
d = zeros(n,m);
for i = 1:n
for j = 1:m
d(i,j) = sum((t(i,:)-r(j,:)).^2);
end
end
% 累积距离矩阵
D = ones(n,m) * realmax;
D(1,1) = d(1,1);
% 动态规划
for i = 1:n
for j = 1:m
if i==1&&j==1
continue;
end
if i>1
D1 = D(i-1,j);
else
D1=realmax;
end
if j>1&&i>1
D2 = D(i-1,j-1);
else
D2 = realmax;
end
if j>1
D3 = D(i-1,j-2);
else
D3 = realmax;
end
D(i,j) = d(i,j) + min([D1,D2,D3]);
end
end
dist = D(n,m);
endmain.m
clear;
t=[1,5,8,10,56,21,32,8];
r=[1,5,8,10,23,56,21,51];
dist=dtw(t,r);通过实际数据测试,该算法只能输入m=n的数据。
得出结果也很大:
dist=4284
无法运行实例1的列向量并得出结果。但代码2可以做到,而且结果准确,Dist=18
代码2
dtw.m
function [Dist,D,k,w,rw,tw]=dtw(r,t,pflag)
% [Dist,D,k,w,rw,tw]=dtw(r,t,pflag)
% Dynamic Time Warping Algorithm
% Dist is unnormalized distance between t and r
% D is the accumulated distance matrix
% k is the normalizing factor
% w is the optimal path
% t is the vector you are testing against
% r is the vector you are testing
% rw is the warped r vector
% tw is the warped t vector
% pflag plot flag: 1 (yes), 0(no)
% Version comments:
[row,M]=size(r);
if (row > M)
M=row; r=r';
end
[row,N]=size(t);
if (row > N)
N=row; t=t';
end
d=sqrt((repmat(r',1,N)-repmat(t,M,1)).^2); %得到两序列对比后的欧式距离矩阵
%sqrt(X)求X所有元素的平方根
%repmat()让r平铺1行N列的矩阵
%所以把r和t的值都撒入坐标矩阵中,相减后分别计算平方后的开方值,也就是欧式距离。
D=zeros(size(d));%按d的大小初始化一个零矩阵给累加矩阵D
D(1,1)=d(1,1);%令第一个累加值等于其欧式距离值,由于D(1,1)只有D(0,0)可以依靠,但D(0,0)=0,所以D(1,1)=0+d(1,1)
for m=2:M
D(m,1)=d(m,1)+D(m-1,1);%在欧式距离矩阵中先计算第一列的每个累加距离
end
for n=2:N
D(1,n)=d(1,n)+D(1,n-1);%在欧式距离矩阵中先计算第一行的每个累加距离
end
for m=2:M
for n=2:N
D(m,n)=d(m,n)+min(D(m-1,n),min(D(m-1,n-1),D(m,n-1))); % this double MIn construction improves in 10-fold the Speed-up.
end
end
Dist=D(M,N);%把最终累加距离给Dist
%实际使用时到这里就可以结束了,只需要得到距离,而后面是可视化的内容
n=N;
m=M;
k=1;
w=[M N];%给出路径终点,开始反推路径
while ((n+m)~=2)
if (n-1)==0
m=m-1;
elseif (m-1)==0
n=n-1;
else
[~,number]=min([D(m-1,n),D(m,n-1),D(m-1,n-1)]);
switch number
case 1
m=m-1;
case 2
n=n-1;
case 3
m=m-1;
n=n-1;
end
end
k=k+1;
w=[m n; w]; %累加最优路径
end
% warped waves
rw=r(w(:,1));
tw=t(w(:,2));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if pflag
% --- Accumulated distance matrix and optimal path
figure('Name','DTW - Accumulated distance matrix and optimal path', 'NumberTitle','off');
main1=subplot('position',[0.19 0.19 0.67 0.79]);
image(D);
cmap = contrast(D);
colormap(cmap); % 'copper' 'bone', 'gray' imagesc(D);
hold on;
x=w(:,1); y=w(:,2);
ind= x==1; x(ind)=1+0.2;
ind= x==M; x(ind)=M-0.2;
ind= y==1; y(ind)=1+0.2;
ind= y==N; y(ind)=N-0.2;
plot(y,x,'-w', 'LineWidth',1);
hold off;
axis([1 N 1 M]);
set(main1, 'FontSize',7, 'XTickLabel','', 'YTickLabel','');
colorb1=subplot('position',[0.88 0.19 0.05 0.79]);
nticks=8;
ticks=floor(1:(size(cmap,1)-1)/(nticks-1):size(cmap,1));
mx=max(max(D));
mn=min(min(D));
ticklabels=floor(mn:(mx-mn)/(nticks-1):mx);
colorbar(colorb1);
set(colorb1, 'FontSize',7, 'YTick',ticks, 'YTickLabel',ticklabels);
set(get(colorb1,'YLabel'), 'String','Distance', 'Rotation',-90, 'FontSize',7, 'VerticalAlignment','bottom');
left1=subplot('position',[0.07 0.19 0.10 0.79]);
plot(r,M:-1:1,'-b');
set(left1, 'YTick',mod(M,10):10:M, 'YTickLabel',10*rem(M,10):-10:0)
axis([min(r) 1.1*max(r) 1 M]);
set(left1, 'FontSize',7);
set(get(left1,'YLabel'), 'String','Samples', 'FontSize',7, 'Rotation',-90, 'VerticalAlignment','cap');
set(get(left1,'XLabel'), 'String','Amp', 'FontSize',6, 'VerticalAlignment','cap');
bottom1=subplot('position',[0.19 0.07 0.67 0.10]);
plot(t,'-r');
axis([1 N min(t) 1.1*max(t)]);
set(bottom1, 'FontSize',7, 'YAxisLocation','right');
set(get(bottom1,'XLabel'), 'String','Samples', 'FontSize',7, 'VerticalAlignment','middle');
set(get(bottom1,'YLabel'), 'String','Amp', 'Rotation',-90, 'FontSize',6, 'VerticalAlignment','bottom');
% --- Warped signals
figure('Name','DTW - warped signals', 'NumberTitle','off');
subplot(1,2,1);
set(gca, 'FontSize',7);
hold on;
plot(r,'-bx');
plot(t,':r.');
hold off;
axis([1 max(M,N) min(min(r),min(t)) 1.1*max(max(r),max(t))]);
grid;
legend('signal 1','signal 2');
title('Original signals');
xlabel('Samples');
ylabel('Amplitude');
subplot(1,2,2);
set(gca, 'FontSize',7);
hold on;
plot(rw,'-bx');
plot(tw,':r.');
hold off;
axis([1 k min(min([rw; tw])) 1.1*max(max([rw; tw]))]);
grid;
legend('signal 1','signal 2');
title('Warped signals');
xlabel('Samples');
ylabel('Amplitude');
end
test.m
clear;
clc;
a=[8 9 1]';
b=[2 5 4 6]';
[Dist,D,k,w,rw,tw] = dtw(a,b,1);
fprintf('最短距离为%d\n',Dist)
fprintf('最优路径为%d\n',w)