day76-day77【代码随想录】单调栈专题

---

前言

1、栈的压入、弹出序列
2、每日温度
3、下一个更大元素 I
4、下一个更大元素 II
5、接雨水
6、状图中最大的矩形
7、最大矩形
8、最大正方形
9、去除重复字母
10、交换一次的先前排列
11、下一个排列

---

一、栈的压入、弹出序列（剑指 Offer 31）【美团3.25笔试】

分析：

大佬清晰题解！！！
太优雅了！！！

class Solution {
    public boolean validateStackSequences(int[] pushed, int[] popped) {
        Stack<Integer> stack = new Stack<>();
        int i=0;
        for(int num:pushed){
            stack.push(num);
            while(!stack.isEmpty() && stack.peek()==popped[i]){
                i++;
                stack.pop();
            }
        }
        return stack.isEmpty();
    }
}

二、每日温度（力扣739）

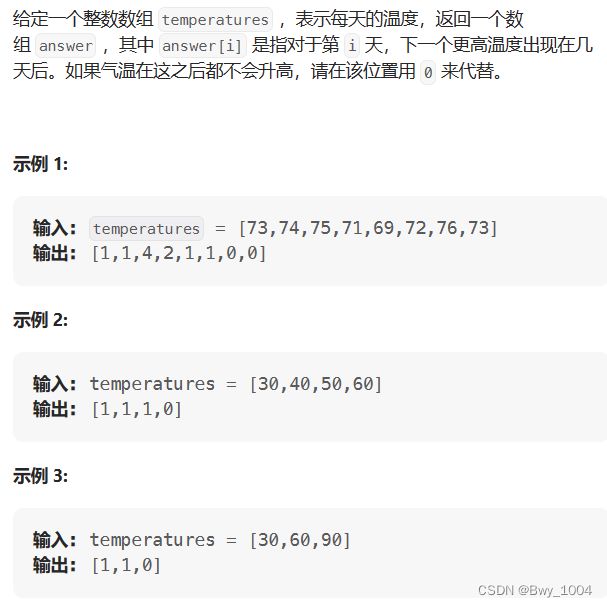
分析：
栈中存放的一定是元素的下标，而不是直接存放元素。因为要计算有多少个值
找右边第一个大于当前元素的下标值，分析清楚什么时候压入栈中，什么时候弹出，栈内元素是递增还是递减的。

class Solution {
public int[] dailyTemperatures(int[] temperatures) {
        //单调栈
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        int[] res = new int[temperatures.length];
        for(int i=1;i<temperatures.length;i++){
            //大小关系 temperatures[stack.peek()]  temperatures[i]
            if( !stack.isEmpty() && temperatures[stack.peek()]>=temperatures[i]){
                //当前遍历元素小于栈顶元素 压入栈中 [下标压入栈中]
                stack.push(i);
            }else{
                //当前遍历元素大于栈顶元素 栈顶元素弹出 并将该元素压入栈中
                while(!stack.isEmpty() && temperatures[stack.peek()]<temperatures[i]){
                    int index = stack.pop();
                    res[index] = i-index;
                }
                stack.push(i);
            }
        }
        return res;
    }
}

三、下一个更大元素 I（力扣496）

class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        int[] res = new int[nums1.length];
        int[] res2= new int[nums2.length];
        res2 = StackIncrement(nums2);
        for(int i=0;i<nums1.length;i++){
            //拿到当前元素 num，去另一个数组中该值对应的下标
            int index = nums1FindInNums2(nums1[i],nums2);
            res[i] = res2[index]==0?-1:nums2[index+res2[index]];
        }
        return res;
    }

    public int[] StackIncrement(int[] nums2){
        Deque<Integer> stack = new LinkedList<>();
        int[] res = new int[nums2.length];
        stack.push(0);
        for(int i=1;i<nums2.length;i++){
            if(!stack.isEmpty() && nums2[i]<=nums2[stack.peek()]){
                stack.push(i);
            }else{
                while(!stack.isEmpty() && nums2[i]>nums2[stack.peek()]){
                    int index = stack.pop();
                    res[index] = i-index;
                }
                stack.push(i);
            }
        }
        return res;
    }

    public int nums1FindInNums2(int num,int[] nums2){
        for(int i=0;i<nums2.length;i++){
            if(num==nums2[i])
                return i;
        }
        return -1;
    }
}

四、下一个更大元素 II（力扣503）

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int[] res = new int[nums.length];
        Arrays.fill(res,-1);
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);

        for(int i=1;i<nums.length*2;i++){
            if(nums[i%nums.length]<= nums[stack.peek()]){
                stack.push(i%nums.length);
            }else{
                while(!stack.isEmpty() && nums[i%nums.length]>nums[stack.peek()]){
                    res[stack.peek()] = nums[i%nums.length];
                    stack.pop();
                }
                stack.push(i%nums.length);
            }
        }
        return res;
    }
}

五、接雨水（力扣42）

分析：
单调栈的经典应用：套用单调栈的模板，找到右边第一个比当前元素大的元素，除此之外，多加了一步找左边第一个比当前元素大的元素【栈内元素 单调递增】，将当前元素弹出之后，栈顶元素就是第一个比当前元素大的值，获取到三个数 left right mid 以及 leftNum rightNum midNum，求对应的面积即可。
ps:会有当前元素值和栈顶元素值相等的情况 可处理可不处理，因为计算面积时，这种情况计算出的面积为0 因此可以不做处理

class Solution {
    public int trap(int[] height) {
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        int res = 0;
        for(int i=1;i<height.length;i++){
            if(!stack.isEmpty() && height[stack.peek()]>= height[i]){
                stack.push(i);
            }
            else{
                while(!stack.isEmpty() && height[stack.peek()]<height[i]){
                    int mid = stack.pop();
                    int midNum = height[mid];
                    if(!stack.isEmpty()){
                        int left = stack.peek();
                        int leftNum = height[left];
                        int rightNum = height[i];
                        int height1 = Math.min(leftNum,rightNum)-midNum;
                        int weight = i-left-1;
                        res += weight*height1;
                    }
                }
                stack.push(i);
            }
        }
        return res;
    }
}

六、状图中最大的矩形（力扣82）

分析：
和接雨水遥相呼应，这道题求当前元素右边出现的第一个比它小的值，以及左边比它小的值，然后再求相应的面积。
注意：那么这道题和接雨水多了一些细节处理 当出现6 7 8 9这样的序列。数据都放栈内了，没法求面积了，因此在heights数组末尾加0，可以让程序继续求面积。 当出现9 8 7 6 这样的序列，9入栈之后，8比9小 此时将9弹出，获取9左边的元素，但是栈为空，所以也没办法求面积，因此需要在heights数组首部加0

class Solution {
public int largestRectangleArea(int[] heights) {
        Stack<Integer> stack = new Stack<Integer>();

        // 数组扩容，在头和尾各加入一个元素
        int [] newHeights = new int[heights.length + 2];
        newHeights[0] = 0;
        newHeights[newHeights.length - 1] = 0;
        for (int index = 0; index < heights.length; index++){
            newHeights[index + 1] = heights[index];
        }
        heights = newHeights;
        stack.push(0);
        int res = 0;
        for (int i = 0; i < heights.length; i++) {
            if (!stack.isEmpty() && heights[stack.peek()] <= heights[i]) {
                stack.push(i);
            } else {
                while (!stack.isEmpty() && heights[stack.peek()] > heights[i]) {
                    //开始出栈
                    int right = i;
                    int mid = stack.peek();
                    int midNum = heights[mid];
                    stack.pop();
                    if (!stack.isEmpty()) {
                        int left = stack.peek();
                        //求面积
                        int weight = right  - left - 1; //宽
                        int height = midNum;
                        res = Math.max(res, weight * height);
                    }
                }
                stack.push(i);
            }
        }
        return res;
    }
}

七、最大矩形（力扣85）

分析：
每一层看作是柱状图，可以套用84题柱状图的最大面积。

第一层柱状图的高度[“1”,“0”,“1”,“0”,“0”]，最大面积为1；

第二层柱状图的高度[“2”,“0”,“2”,“1”,“1”]，最大面积为3；

第三层柱状图的高度[“3”,“1”,“3”,“2”,“2”]，最大面积为6；

第四层柱状图的高度[“4”,“0”,“0”,“3”,“0”]，最大面积为4；

ps:

        if (matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }

class Solution {
   public int maximalRectangle(char[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int[] area = new int[matrix.length];
        int[] heights = new int[matrix[0].length];
        for(int i=0;i<matrix.length;i++){
            for(int j=0;j<matrix[0].length;j++){
                if(matrix[i][j]=='1'){
                    heights[j] += '1'-'0';
                }else{
                    heights[j] = 0;
                }
            }
            //放进单调栈 heights
            area[i] = ZhuZhuangTuMaxArea(heights);
        }
        int res = 0;
        //遍历area数组找最大值
        for(int i=0;i<area.length;i++){
            res = Math.max(res,area[i]);
        }
        return res;

    }

    public int ZhuZhuangTuMaxArea(int[] heights){
        Deque<Integer> stack = new LinkedList<Integer>();
        //数组扩容
        int[] newHeights = new int[heights.length+2];
        newHeights[0] = 0;
        newHeights[newHeights.length-1]=0;
        for(int i=0;i<heights.length;i++){
            newHeights[i+1]= heights[i];
        }
        heights = newHeights;
        stack.push(0);
        int res = 0;
        for(int i=0;i<heights.length;i++){
            if(!stack.isEmpty() && heights[i]>=heights[stack.peek()]){
                stack.push(i);
            }
            else{
                while(!stack.isEmpty() && heights[i]<heights[stack.peek()]){
                    int mid = stack.pop();
                    int midNum = heights[mid];
                    if(!stack.isEmpty()){
                        int left = stack.peek();
                        int weight = i-left-1;
                        res = Math.max(res,weight*midNum);
                    }
                }
                stack.push(i);
            }
        }
        return res;
    }
}

八、最大正方形（力扣221）

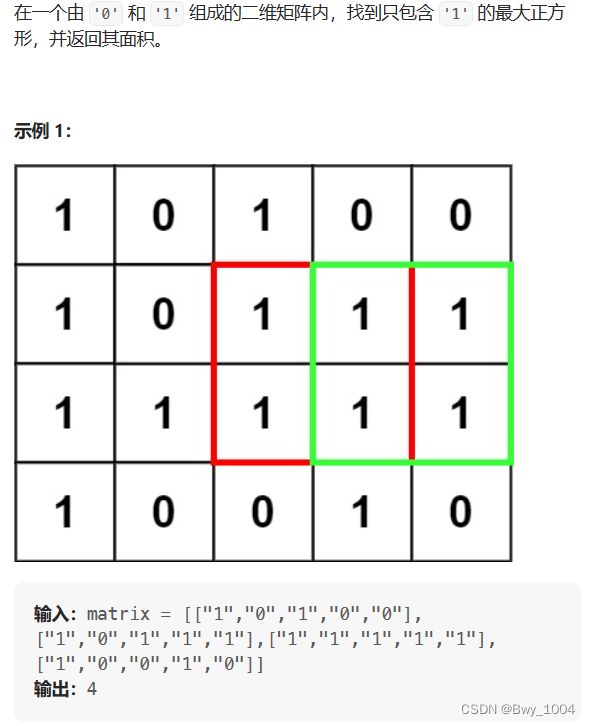
ps：只要想清楚dp数组表示 正方形的最大边长 就比较好求解了

动规五部曲：
1、dp数组以及下标含义
dp[i][j] :表示 matrix矩阵 i行j列时正方形的最大边长
2、初始化

        for(int i=0;i<matrix.length;i++){
            dp[i][0] = matrix[i][0]=='1'?1:0;
        }
        for(int j=0;j<matrix[0].length;j++){
            dp[0][j] = matrix[0][j]=='1'?1:0;
        }

3、递推公式
dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1

4、遍历顺序
从左到右

class Solution {
    public int maximalSquare(char[][] matrix) {
        int[][] dp = new int[matrix.length][matrix[0].length];

        //初始化
        for(int i=0;i<matrix.length;i++){
            dp[i][0] = matrix[i][0]=='1'?1:0;
        }
        for(int j=0;j<matrix[0].length;j++){
            dp[0][j] = matrix[0][j]=='1'?1:0;
        }
        //递推公式

        for(int i=1;i<matrix.length;i++){
            for(int j=1;j<matrix[0].length; j++){
                if(matrix[i][j]=='1'){
                    dp[i][j] = Math.min(dp[i-1][j],Math.min(dp[i][j-1],dp[i-1][j-1]))+1;
                }
            }
        }
        //找dp数组中的最大值
        int res = 0;
        for(int i=0;i<matrix.length;i++){
            for(int j=0;j<matrix[0].length;j++){
                res = Math.max(res,dp[i][j]);
            }
        }
        return res*res;

    }
}

九、去除重复字母（力扣316）

分析：
首先需要记录每一个字符出现的次数
分析清楚什么时候放入栈中什么时候弹出，需要借助一个额外的数组，去记录当前元素在栈中是否出现过。

如果当前元素在栈中已经出现过了，那么相当于舍弃当前元素，需要将其对应的出现次数-1，
如果当前元素在栈中没有出现过，那么还需要考虑什么情况下放入栈中

• 若栈顶元素的字典排序大于当前元素并且栈顶元素的出现次数是大于1的，也就是说之后还会遇到这个元素，此时我们可以把栈顶元素弹出。 **注意：**弹出之后需要将其对应的状态一一修改 （出现次数要-1，该元素要更改为没有在栈中出现过）
• 上述过程结束后，再将当前元素放入栈中

class Solution {
public String removeDuplicateLetters(String s) {
        Deque<Integer> stack = new LinkedList<>();
        char[] ss = s.toCharArray();
        Map<Character,Integer> map = new HashMap<>();
        //统计出现的次数
        for(int i=0;i<ss.length;i++){
            map.put(ss[i],map.getOrDefault(ss[i],0)+1);
        }
        boolean[] exits = new boolean[26];
        stack.push(0);
        exits[ss[0]-'a']=true;

        for(int i=1;i<ss.length;i++){
            char c = ss[i];
            if(!exits[c-'a']){
                while(!stack.isEmpty() && ss[stack.peek()]>c && map.get(ss[stack.peek()])>1){
                    int temp = stack.pop();
                    exits[ss[temp]-'a']=false;
                    map.put(ss[temp],map.get(ss[temp])-1);
                }
                stack.push(i);
                exits[c-'a']=true;

            }else{
                map.put(c,map.get(c)-1);
            }
        }

        StringBuffer res = new StringBuffer();
        for(int ch : stack){
            res.append(ss[ch]);
        }
        return res.reverse().toString();
    }
}

---

每日一题day77：交换一次的先前排列（力扣1053）

分析：
注意：从后往前遍历，当出现逆序时，就说明肯定会存在比当前字典序小的排列，当出现arr[i] > arr[i+1] 时，我们就需要交换 arr[i]所对应的值，那么具体和谁进行交换？从i+1开始遍历 去找arr[j] 如果没有出现逆序的情况，直接返回原数组即可

class Solution {
    public int[] prevPermOpt1(int[] arr) {
        int index = -1;
        int max = -1;
        for(int i=arr.length-2;i>=0;i--){
            if(arr[i]>arr[i+1]){
                //出现逆序
                for(int j = i+1;j<arr.length;j++){
                    if(arr[i]>arr[j]){
                        if(arr[j]>max){
                            max = arr[j];
                            index = j;
                        }
                    }
                }
                int temp = arr[i];
                arr[i] = arr[index];
                arr[index] = temp;
                return arr;
            }
        }
        return arr;
    }
}

每日一题类似题目：下一个排列（力扣31）

分析：
这道题目和上一道题目比较类似，但是需要处理的细节稍微多一点。
想找到比当前字典序列大的组合

• 什么时候进行交换？ 倒序遍历，当nums[i]
• 和谁进行交换？ 从i+1开始遍历 找到 右边最小的值nums[j] 并且还要求nums[j]>nums[i] ，此时交换
• 交换之后还需要进行反转 如下图所示。
  
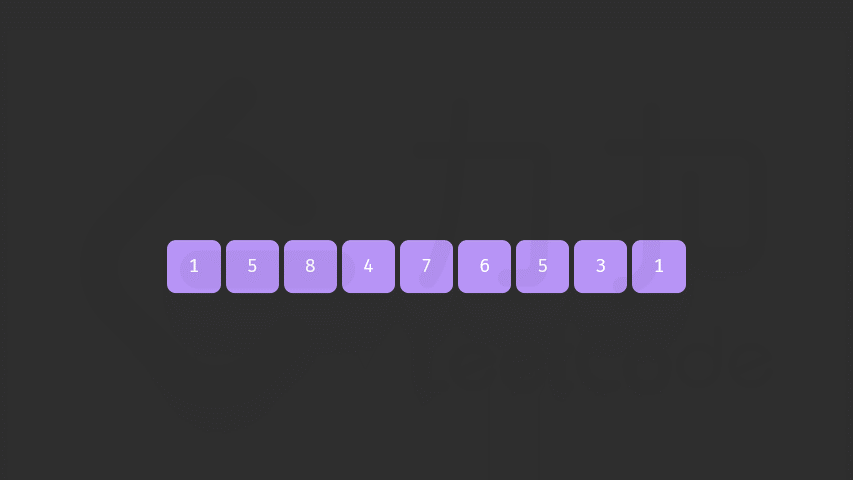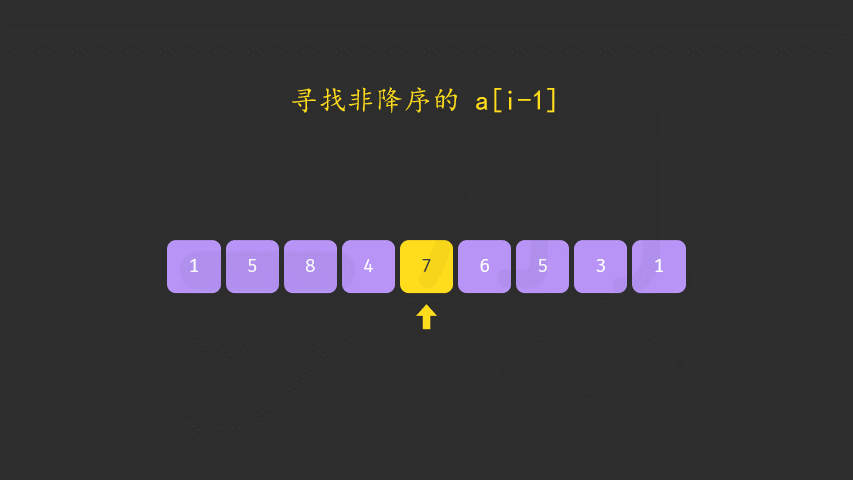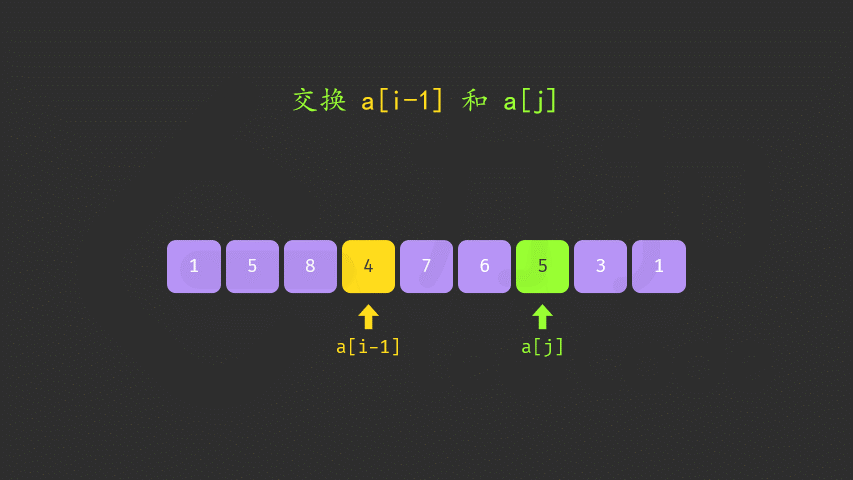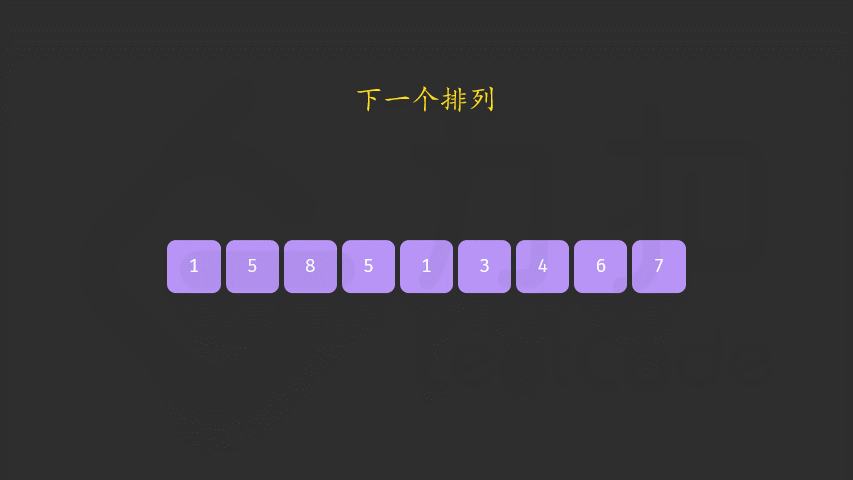
• 细节一：最后的字符反转 容易忘记
• 细节二：当min>=nums[j] 时需要更新最小值的下标 等于时也需要更新

                        if(min>=nums[j]){
                            min = nums[j];
                            index = j;
                        }

例如：2,3,1,3,3
1、首先找到nums[i] 即nums[2] 2、找到和谁交换 j=3 开始 min 更新为3 对应index 更新为3（下标）
j=4 min=nums[j] 也需要更新 min =3 index = 4
3、交换 2 3 3 3 1;
4、从i+1开始翻转 2 3 3 1 3

若 j=4 min=nums[j] 没有更新 min =3 index = 3
此时交换 2 3 3 1 3
再进行翻转 2 3 3 3 1(×) 结果出错

class Solution {
    public void nextPermutation(int[] nums) {
        //逆序遍历 一定需要搞清楚哪个值需要交换，什么条件下才能交换
        //以及和谁交换两个问题
        int i=0;
        for(i=nums.length-2;i>=0;i--){
            if(nums[i]<nums[i+1]){ //说明会有比当前字典序大的结果出现
                //需要进行交换
                //找右边的一个最小值 nums[j]>nums[i]
                int min = Integer.MAX_VALUE;
                int index = -1;
                for(int j=i+1;j<nums.length;j++){
                    if(nums[j]>nums[i]){
                        if(min>=nums[j]){
                            min = nums[j];
                            index = j;
                        }
                    }
                }
                int temp = nums[i];
                nums[i] = nums[index];
                nums[index] = temp;
                break;
            }
        }
        reverse(nums, i + 1);
    }

    public void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    public void reverse(int[] nums, int start) {
        int left = start, right = nums.length - 1;
        while (left < right) {
            swap(nums, left, right);
            left++;
            right--;
        }
    }
}