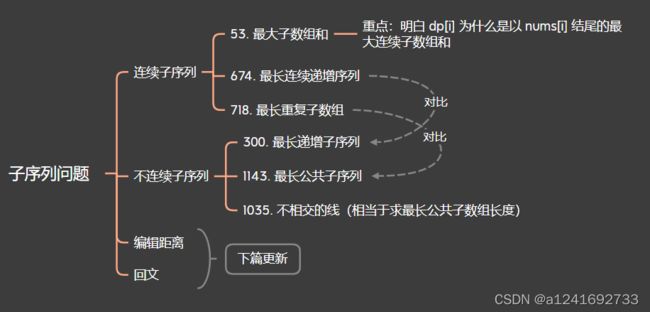
Leetcode 刷题笔记(二十八) ——动态规划篇之子序列问题：连续子序列和不连续子序列

系列文章目录

一、 数组类型解题方法一：二分法
二、数组类型解题方法二：双指针法
三、数组类型解题方法三：滑动窗口
四、数组类型解题方法四：模拟
五、链表篇之链表的基础操作和经典题目
六、哈希表篇之经典题目
七、字符串篇之经典题目
八、字符串篇之 KMP
九、解题方法：双指针
十、栈与队列篇之经典题目
十 一、栈与队列篇之 top-K 问题
十 二、二叉树篇之二叉树的前中后序遍历
十 三、二叉树篇之二叉树的层序遍历及相关题目
十 四、二叉树篇之二叉树的属性相关题目
十 五、 二叉树篇之二叉树的修改与构造
十 六、 二叉树篇之二叉搜索树的属性
十 七、二叉树篇之公共祖先问题
十 八、二叉树篇之二叉搜索树的修改与构造
十 九、回溯算法篇之组合问题
二 十、回溯算法篇之分割、子集、全排列问题
二十一、贪心算法篇之入门题目
二十二、贪心算法篇之进阶题目
二十三、动态规划篇之基础题目
二十四、动态规划篇之背包问题：01背包
二十五、动态规划篇之背包问题：完全背包
二十六、动态规划篇之经典问题：打家劫舍
二十七、动态规划篇之买股票问题（一）
更新中 … …

---

前言

刷题路线来自 ：代码随想录

题录

53. 最大子数组和

Leetcode 链接

题解：
状态 dp[i]: 区间 [0, i] 以 i 结尾的最大子数组和。
递推公式： dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]) 这里的第 i 个状态只与 第 i - 1 个状态有关
以 nums[i] 结尾的子数组最大和 = max(以 nums[i - 1] 结尾的最大子数组和加上 nums[i], nums[i])
返回值另外记录： res

虽然这道题简单，但是不明白下边这个问题，做完后还是会感觉迷迷糊糊。
为什么 dp[i] 的状态 不能表示 区间 [0, i] 的最大子数组和（重点），这样的化返回值就是 dp 数组最后一个元素，不用另外记录返回值，还方便？
因为如果这样的话，状态 dp[i] 不知道前边状态表示的最大连续子数组和表示的子数组 与 新增的 nums[i] 是不是连续的，进而无法得到当前状态的最大连续子数组和。

明白了这个道理，对于下边的子序列问题，到底是将 dp 数组的最后一个元素作为返回值还是另外记录返回值，以及连续和不连续的区别就一目了然了。

class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int res = nums[0];
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

674. 最长连续递增序列

Leetcode 链接

题解：
子序列连续，另外记录返回值
状态 dp[i]：表示以 新增数 nums[i] 结尾的最大连续子数组长度
递推公式：满足 nums[i] > nums[i - 1] ，dp[i] = dp[i - 1] + 1 即可

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int res = 1;
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > nums[i - 1]) {
                dp[i] = dp[i - 1] + 1;
                res = Math.max(res, dp[i]);
            }
        }
        return res;
    }
}

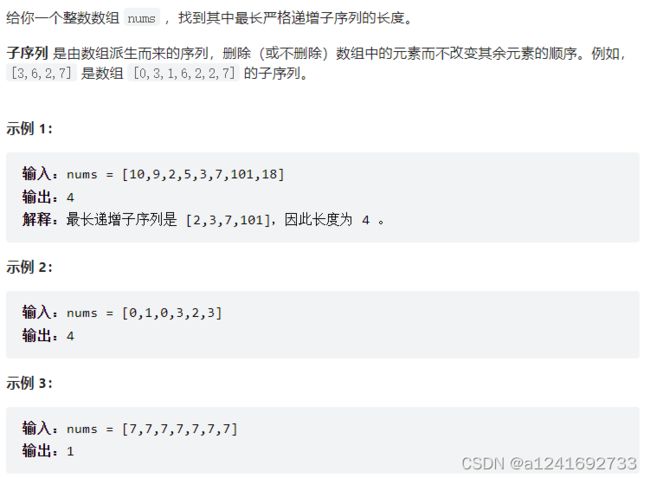
300. 最长递增子序列

Leetcode 链接

题解：
这里还是需要另外记录返回值，为什么呢？
因为这道题的子序列不连续，第 i 个状态不止和连续的第 i - 1 状态有关，还和前边所有不连续的第 j 个状态优化。dp[j] 需要保存以 j 结尾的最长不连续递增子序列长度，这样第 i 个状态，才能根据判断 nums[i] > nums[j] 来确定 dp[i] 的值，这里的 i 和 j 不一定连续，但是比较的时候应该放在一起看。
状态 dp[i]：以 i 结尾的最长不连续递增子序列长度

class Solution {
    public int lengthOfLIS(int[] nums) {
        int len = nums.length;
        int[] dp = new int[len];
        // 初始化
        Arrays.fill(dp, 1);
        int res = 1;
        for (int i = 1; i < len; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            // nums 数组以任意下标结尾的子序列都有可能为最长子序列，所以每个子序列遍历完都要进行返回值的更新
            if (dp[i] > res) res = dp[i];
        }
        return res;
    }
}

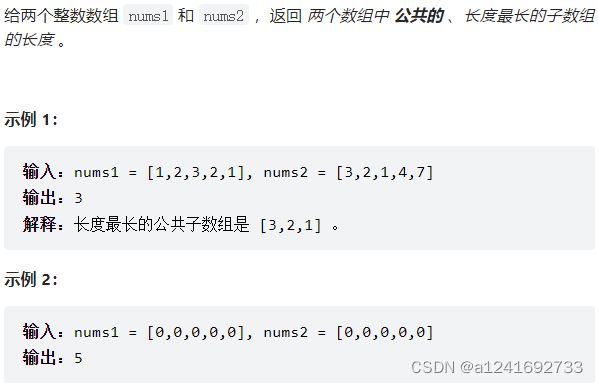
718. 最长重复子数组

Leetcode 链接

题解：

题解：
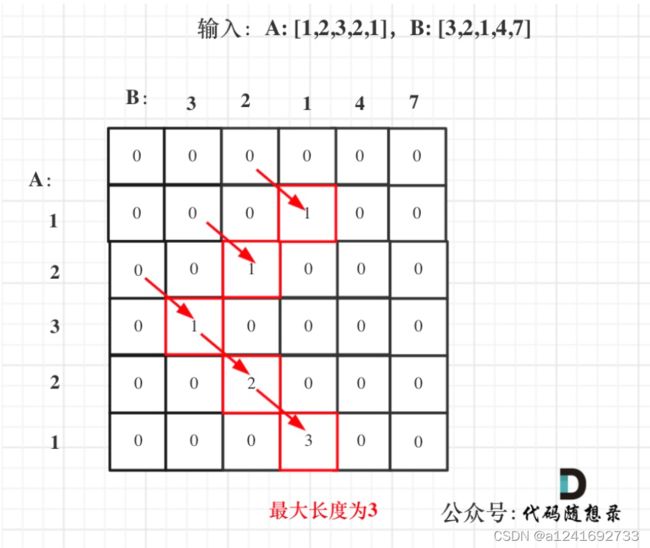
状态 dp[i][j]：以 nums1[i - 1] 和 nums2[j - 1] 结尾的子数组的最长公共连续子序列长度。
每个dp[i][j]状态都有第dp[i - 1][j - 1] 个状态决定，保证了两个子数组都为连续的，返回另外记录

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int row = nums1.length;
        int col = nums2.length;
        int[][] dp = new int[row + 1][col + 1];
        int res = 0;
        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= col; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                    res = Math.max(res, dp[i][j]);
                }
            }
        }
        return res;
    }
}

空间优化：使用一维滚动数组

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int row = nums1.length;
        int col = nums2.length;
        int[] dp = new int[col + 1];
        int res = 0;
        for (int i = 1; i <= row; i++) {
            for (int j = col; j >= 1; j--) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[j] = dp[j - 1] + 1;
                    res = Math.max(res, dp[j]);
                } else {
                    dp[j] = 0;
                }
            }
        }
        return res;
    }
}

1143. 最长公共子序列

Leetcode 链接

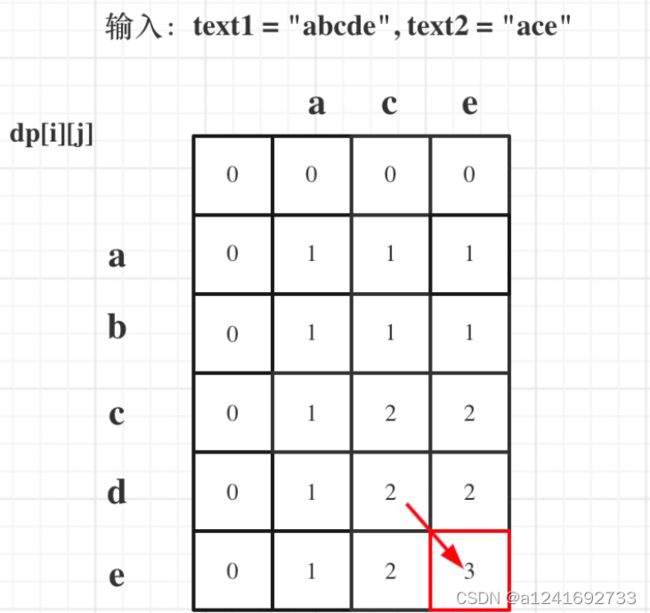
题解：
状态 dp[i][j]：表示[0, i] 子序列1 和 [0, j] 子序列2 的最长公共不连续子序列长度
”abcde“ 和 ”ace“ 在最后一个状态发现结尾都为 e ,此时该状态的值（最长不连续公共子序列）会与"abcd" 和 ”ac“ 状态有关，也就是 dp[i][j] = dp[i - 1][j - 1] + 1，这里和上一个状态是连续的，也就是以 i - 1 和 j - 1 结尾的状态
”abcd“ 和 ”ace“ 时 在最后一个状态结尾不相等，该状态的值与 ”abcd“ 和， ”ac“、”abc“ 和 ”ace“ 两个状态有有关也就是 dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1])，这里的状态一定是不连续的

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int row = text1.length();
        int col = text2.length();
        int[][] dp = new int[row + 1][col + 1];
        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= col; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[row][col];
    }
}

1035. 不相交的线

Leetcode 链接


题解：
同上题，其实是求最长公共子数组

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int row = nums1.length;
        int col = nums2.length;
        int[][] dp = new int[row + 1][col + 1];
        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= col; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[row][col];
    }
}