LeetCode刷题---707. 设计链表（双向链表-带头尾双结点）

• 所属专栏：【LeetCode题解（持续更新中）】

• 作  者：我是夜阑的狗

• 个人简介：一个正在努力学技术的码仔，专注基础和实战分享 ，欢迎咨询！

• 欢迎大家：这里是CSDN，我总结知识的地方，喜欢的话请三连，有问题请私信
  
  

您的点赞、关注、收藏、评论，是对我最大的激励和支持！！！

---

前言

  大家好，又见面了，我是夜阑的狗，本文是专栏【LeetCode题解】专栏的第11篇文章，主要讲解是LeetCode707. 设计链表（双向链表-带头尾双结点）。
  专栏地址：【LeetCode题解（持续更新中）】， 此专栏是我是夜阑的狗对LeetCode问题的讲解，希望能够加深自己的印象，以及帮助到其他的小伙伴。
  如果文章有什么需要改进的地方还请大佬不吝赐教。

---

一、编程题：707. 设计链表（双向链表-带头尾双结点）

1.题目描述

  设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性：val 和 next。val 是当前节点的值，next 是指向下一个节点的指针/引用。如果要使用双向链表，则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。LeetCode题目链接。
  在链表类中实现这些功能：

• get(index)：获取链表中第 index 个节点的值。如果索引无效，则返回-1。
• addAtHead(val)：在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
• addAtTail(val)：将值为 val 的节点追加到链表的最后一个元素。
• addAtIndex(index,val)：在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果index小于0，则在头部插入节点。
• deleteAtIndex(index)：如果索引 index 有效，则删除链表中的第 index 个节点。

2.示例1：

MyLinkedList linkedList = new MyLinkedList();
linkedList.addAtHead(1);
linkedList.addAtTail(3);
linkedList.addAtIndex(1,2); //链表变为1-> 2-> 3
linkedList.get(1); //返回2
linkedList.deleteAtIndex(1); //现在链表是1-> 3
linkedList.get(1); //返回3

3.提示：

• 0 <= index, val <= 1000
• 请不要使用内置的 LinkedList 库。
• get, addAtHead, addAtTail, addAtIndex 和 deleteAtIndex 的操作次数不超过 2000。

---

二、解题思路

  本题单纯就是对数据结构链表构成的考察，由于题中涉及到一些对中间变量的操作，所以采用双向链表来进行解决，加上贪心算法来进行查询位置加快运行速度。不过这里关键点还是在于要定义好链表的边界，这一点要理清楚。不然在编写过程容易缺失部分数据处理（本人踩的坑）。基本上能完成双向链表之后都可以写顺利写单向链表，不然也可以先写出单向链表，然后在写根据单向写双向，多写几遍印象更深刻点。

1.思路

解决方法1（个人想法）：

• Step 1.创建双向链表结点（有前驱后继），在MyLinkedList中创建头尾双结点，以便后续方便处理中间变量;
• Step 2.涉及index操作时，采用贪心算法使其从最近的一边开始遍历（注：一定要对index进行安全处理，以防数据无效）;
• Step 3.编写Nodeshow函数打印链表数据，以便编写过程中进行调试;

2.复杂度分析：

时间复杂度：涉及 index 的相关操作复杂度为 O(index)；其余操作均为 O(1)
空间复杂度：O(n)

3.算法图解（双向链表）

红色部分代表待操作元素。（注：本人不会做成流程动画，希望会的朋友可以私信我指点一二，说个软件名字也可以，谢谢）
头插法（尾插法）：

• Step 1. 要先处理插入结点1的指向，分别把结点1的前驱后继指向
• Step 2. 再来解决原先结点的指向，如图所示把head->next和end->prev指向1，即插入完成。

（注： 这里1，2步不能搞混，要先执行第一步在执行第二步，反过来则会出错，可以尝试一下并打log体会）

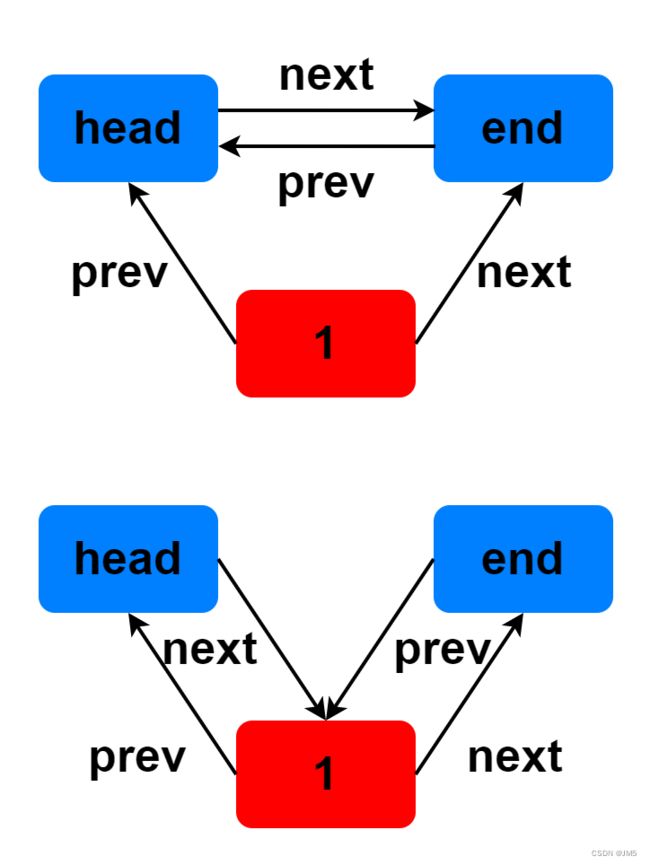
删除操作：

• Step 1. 同理，要先处理删除结点1的前后结点指向，如图所示，分别把head->next指向end，end->prev指向head即可；
• Step 2. 最后在把结点1删除，即删除完成。

（注： 这里1，2步不能搞混，要先执行第一步在执行第二步，反过来则会出错，可以尝试一下并打log体会）

---

三、代码实现

。每个代码块都写了注释，方便理解，代码还可以改进；
代码如下（示例）：
解法一：

class MyLinkedList {
    //创建头结点,尾结点
    private Node head, end;
    //链表长度
    private int length;

    public MyLinkedList() {
        // 链表初始化
        this.head = new Node(-1, null, null);
        this.end = new Node(-1, null, null);

        // 连接链表初始节点
        this.head.setNode(null, this.end);
        this.end.setNode(this.head, null);

        this.length = 0;
    }
    
    //获取当前元素
    public int get(int index) {
        //安全处理
        if(index >= 0 && index+1 <= this.length){
            //当前结点
            // 使用贪心每次都从最近的地方开始找
            Node temp = index <= this.length/2 ? this.head : this.end;
            // 可优化代码将其抽离成模块
            if(index <= this.length/2){
                // 从头结点
                for(int i = 0; i <= index; i++){
                    temp = temp.next;
                }
            }else{
                for(int i = 0; i <= this.length - index - 1; i++){
                    temp = temp.prev;
                }
            }
            return temp.val;
        }
        return -1;
    }
    
    //头插法
    public void addAtHead(int val) {
        Node temp = new Node(val,null,null);
        // 第一步先处理插入的元素指向
        temp.next = this.head.next;
        temp.prev = this.head;
        // 第二步在处理原先的元素指向
        
        this.head.next.prev = temp;
        this.head.next = temp;
        this.length++;
        // Nodeshow();
    }
    
    //尾插法
    public void addAtTail(int val) { 
        Node temp = new Node(val,null,null);
        // 双向链表
        // 第一步先处理插入的元素指向
        temp.next = this.end;
        temp.prev = this.end.prev;
        // 第二步在处理原先的元素指向
        this.end.prev.next = temp;
        this.end.prev = temp;

        this.length++;
        // Nodeshow();
    }
    
    // 在第index个节点之前添加值为val的节点
    public void addAtIndex(int index, int val) {
        //安全处理
        if(index >= 0 && index <= this.length){
            //当前结点
            Node temp = index <= this.length/2 ? this.head : this.end;
            Node temp_node = new Node(val, null,null);

            // 使用贪心每次都从最近的地方开始找
            // 可优化代码将其抽离成模块
            if(index <= this.length/2){
                // 从头结点开始寻找要插入的位置
                for(int i = 0; i < index; i++){
                    temp = temp.next;
                }
                //插入结点 temp结点为要插入位置的前一个结点
                temp_node.next = temp.next;
                temp_node.prev = temp;

                temp.next.prev = temp_node;
                temp.next = temp_node;
            }else{
                // 从尾节点开始找到要插入的位置
                for(int i = 0; i <= this.length - index - 1; i++){
                    temp = temp.prev;
                }
                // 插入结点 temp结点为要插入位置的当前结点
                temp_node.next = temp;
                temp_node.prev = temp.prev;

                temp.prev.next = temp_node;
                temp.prev = temp_node;                
            }

            this.length++;
            // Nodeshow();
        }
    }
    
    public void deleteAtIndex(int index) {
        //安全处理
        // System.out.println("this.length = " + this.length);
        if(index >= 0 && index+1 <= this.length){
            Node temp = this.head;
  
            //双向链表 找到删除结点
            for(int i = 0; i <= index; i++){
                temp = temp.next;
            }
            temp.next.prev = temp.prev;
            temp.prev.next = temp.next;

            this.length--;
            // Nodeshow();
        }
        
    }

    public void Nodeshow(){
        Node temp = head;
        while(temp.next != null){
            System.out.print(temp.val + " ");
            temp = temp.next;
        }
        System.out.print(temp.val + " ");
        System.out.println();
    }
}

//先创建结点对象，双向链表
public class Node{
    public int val;
    public Node prev; //前驱结点
    public Node next; //后续结点

    public Node(int val){
        this.val = val;
        this.prev = null;
        this.next = null;
    }

    public Node(int val, Node prev,Node next){
        this.val = val;
        this.prev = prev;
        this.next = next;
    }

    public void setNode(Node prev, Node next){
        this.prev = prev;
        this.next = next;
    }
}

提交结果：

三、单向链表代码实现

class MyLinkedList {
    //创建头结点,尾结点
    private Node head;
    //链表长度
    private int length;

    public MyLinkedList() {
        //链表初始化
        this.head = new Node(-1, null);
        this.end = new Node(-1, null);
        this.length = 0;
    }
    
    //获取当前元素
    public int get(int index) {
        //安全处理
        if(index >= 0 && index+1 <= this.length){
            //当前结点
            Node temp = this.head;
            for(int i = 0; i <= index; i++){
                temp = temp.next;
            }
            return temp.val;
        }
        return -1;
    }
    
    //头插法
    public void addAtHead(int val) {
        Node temp = new Node(val,null);
        temp.next = this.head.next;
        this.head.next = temp;
        this.length++;
        // Nodeshow();
    }
    
    //尾插法
    public void addAtTail(int val) { 
        Node temp = new Node(val,null);
        Node temp_head = this.head;
        //找到尾部
        while(temp_head.next != null) temp_head = temp_head.next;
        temp_head.next = temp;
        this.length++;
        // Nodeshow();
    }
    
    public void addAtIndex(int index, int val) {
        //安全处理
        if(index >= 0 && index <= this.length){
            //当前结点
            Node temp = this.head;
            Node temp_node = new Node(val, null);
            for(int i = 0; i < index; i++){
                temp = temp.next;
            }
            //插入结点
            temp_node.next = temp.next;
            temp.next = temp_node;
            this.length++;
            // Nodeshow();
        }
    }
    
    public void deleteAtIndex(int index) {
        //安全处理
        // System.out.println("this.length = " + this.length);
        if(index >= 0 && index+1 <= this.length){
            Node temp = this.head;
            //找到删除结点的前一个结点
            for(int i = 0; i <= index-1; i++){
                temp = temp.next;
            }
            // System.out.print(temp.val + " === ");
            temp.next = temp.next.next;
            this.length--;
            // Nodeshow();
        }
        
    }

    public void Nodeshow(){
        Node temp = head;
        while(temp.next != null){
            System.out.print(temp.val + " ");
            temp = temp.next;
        }
        System.out.print(temp.val + " ");
        System.out.println();
    }
}

//先创建结点对象
public class Node{
    public int val;
    public Node next;

    public Node(int val){
        this.val = val;
    }

    public Node(int val, Node next){
        this.val = val;
        this.next = next;
    }
}

---

总结

以上就是今天要讲的内容，本题单纯就是对数据结构链表构成的考察，由于题中涉及到一些对中间变量的操作，所以采用双向链表来进行解决，加上贪心算法来进行查询位置加快运行速度。不过这里关键点还是在于要定义好链表的边界，这一点要理清楚。不然在编写过程容易缺失部分数据处理（本人踩的坑）。所以就赶紧记录一下这时刻。

感谢观看，如果有帮助到你，请给题解点个赞和收藏，让更多的人看到。

也欢迎你，关注我。

原创不易，还希望各位大佬支持一下，你们的点赞、收藏和留言对我真的很重要！！！ 最后，本文仍有许多不足之处，欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正！

更多专栏订阅:

• 【LeetCode题解（持续更新中）】
• 【Java Web项目构建过程】
• 【数字图像处理】
• ⚽ 【JavaScript随手笔记】
• 【大数据学习笔记（华为云）】
• 【程序错误解决方法（建议收藏）】
• 【软件安装教程】

订阅更多，你们将会看到更多的优质内容！！