Java——二叉树的最近公共祖先及二叉搜索树介绍

目录

二叉树的最近公共祖先

题目 

思路一：如果给定的是一颗二叉搜索树，

思路二：假设是孩子双亲表示法

 二叉搜索树

定义Node类

查找

删除

插入

---

二叉树的最近公共祖先

题目 

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

提示：

树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中

思路一：如果给定的是一颗二叉搜索树，

二叉搜索树：中序遍历的大小是有序的，根节点的左树都比根节点的小，根节点的右树都比根节点大。

 

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //先根据二叉搜索树来写
        if(root==null) return null;
        if(root==p||root==q) return root;
        TreeNode leftT=lowestCommonAncestor(root.left,p,q);
        TreeNode rightT=lowestCommonAncestor(root.right,p,q);
        if(leftT!=null&&rightT!=null){
            return root;
        }else if(leftT!=null){
            return leftT;
        }else{
            return rightT;

        }
        
    }
}

思路二：假设是孩子双亲表示法

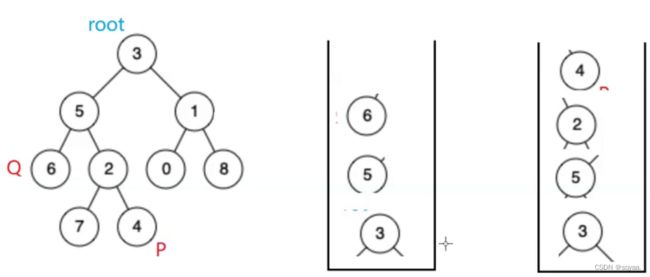
就相当于链表求交点，但是我们的表示中没有双亲结点，因此我们引入两个栈。

1.用两个栈 存储root->q,root->p的路径；

2.求栈的大小；

3.让栈中多的元素出差值个元素；

4.开始出栈，直到栈顶元素相同，就是公共祖先；

如何去找到从根节点到一个指定节点的路径？ 

class Solution {
    //root根结点，node:指定的节点，stack:存放根节点到指定节点的路径
    public boolean getPath(TreeNode root,TreeNode node ,Stack stack){
        if(root==null||node==null) return false;
        stack.push(root);
        if(node==root) return true;
        boolean flg=getPath(root.left,node,stack);
        if(flg==true) return true;//找到啦
      flg=getPath(root.right,node,stack);
        if(flg==true) return true;//找到啦
        stack.pop();
        return false;

    }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null) return null;
        Stack stack1=new Stack<>();
        getPath(root,p,stack1);
        Stack stack2=new Stack<>();
        getPath(root,q,stack2);
        int size1=stack1.size();
        int size2=stack2.size();
        if(size1>size2){
            int size=size1-size2;
            while(size!=0){
                stack1.pop();
                size--;
            }
            while(!stack1.isEmpty()&&!stack2.isEmpty()){
                //直接判断地址
                if(stack1.peek()==stack2.peek()){
                    return stack1.pop();
                }else{
                    stack1.pop();
                    stack2.pop();
                }
            }

        }else{
            int size=size2-size1;
            while(size!=0){
                stack2.pop();
                size--;
            }
            while(!stack1.isEmpty()&&!stack2.isEmpty()){
                //直接判断地址
                if(stack1.peek()==stack2.peek()){
                    return stack2.pop();
                }else{
                    stack1.pop();
                    stack2.pop();
                }
            }
        }
        return null;



    }
}

 二叉搜索树

是空树或者：

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

它的左右子树也分别为二叉搜索树

定义Node类

class Node{
    public int val;
    public Node left;
    public Node right;
    public Node(int val){
        this.val=val;
    }
}

查找

  public Node root=null;
    public Node search(int key){
        Node cur = root;
        if(cur.valkey){
            cur = cur.left;
        }else{
            return cur;
        }
        return null;
    }

删除

设待删除结点为 cur, 待删除结点的双亲结点为 parent

1. cur.left == null

1. cur 是 root ，则 root = cur.right

2. cur 不是 root ， cur 是 parent.left ，则 parent.left = cur.right

3. cur 不是 root ， cur 是 parent.right ，则 parent.right = cur.right

2. cur.right == null

1. cur 是 root ，则 root = cur.left

2. cur 不是 root ， cur 是 parent.left ，则 parent.left = cur.left

3. cur 不是 root ， cur 是 parent.right ，则 parent.right = cur.left

3. cur.left != null && cur.right != null

1. 需要使用 替换法 进行删除，即在它的右子树中寻找中序下的第一个结点 ( 关键码最小 ) ，用它的值填补到被

删除节点中，再来处理该结点的删除问题

   //要删除节点，你需要知道这个节点的父节点
    //当要删除的节点的左节点为空
    //一般删除节点都是删除叶子节点

    public void f(Node cur,Node parent){
        if(cur.left==null){//当删除的节点左边没有节点
            if(cur==root){
                root=cur.right;
            }else if(cur==parent.left){
                parent.left=cur.right;

            }else{
                parent.right=cur.right;

            }
        }else if(cur.right==null){
            if(cur==root){
                root=cur.left;
            }else if(cur==parent.left){
                parent.left=cur.left;
            }else{
                parent.right=cur.left;
            }
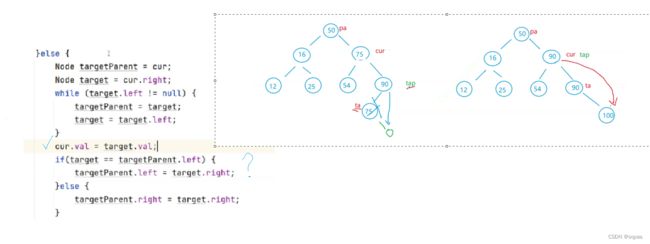
        }else{//左右节点都不是空
            //相当于在右树中找一个较小值换到那个位置
            //或者就是在左树中找较大值
            //
            Node targetParent=cur;
            Node target=cur.right;
            while(target.left!=null){
                targetParent=target;
                target=target.left;
            }
            cur.val=target.val;
            if(target==targetParent.left){
                targetParent.left=target.right;
            }else{
                targetParent.right=target.right;
            }
        }


    }
    public void remove(int key){
        Node cur=root;
        Node parent=null;
        while(cur!=null){
            if(cur.val==key){
                f(cur,parent);
                break;
            }else if(cur.val

插入

   //二叉搜索树插入的数据一定是在叶子节点
    //1.cur,parent来找到val需要存储的位置
    //2.parent.val比较大小，确定格式在左边还是右边进行插入
    public  boolean insert(int val){
        if(root == null){
            root = new Node(val);
            return true;

        }
        Node cur = root;
        Node parent = null;
        //找到parent的位置
        while(cur!=null){
            if(cur.val