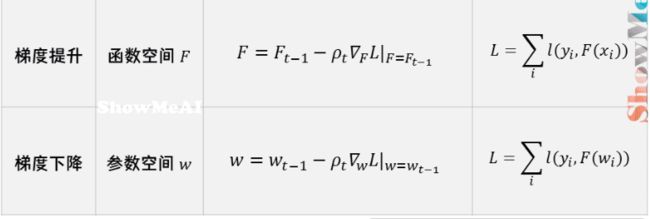GBDT模型详解
GBDT算法
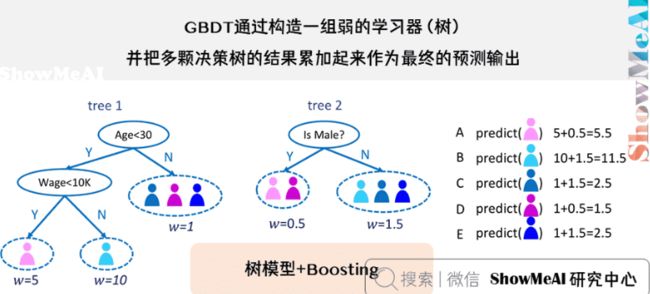
GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,是一种迭代的决策树算法,又叫MART(Multiple Additive Regression Tree),它通过构造一组弱的学习器(树),并把多颗决策树的结果累加起来作为最终的预测输出。该算法将决策树与集成思想进行了有效的结合。
Boosting核心思想
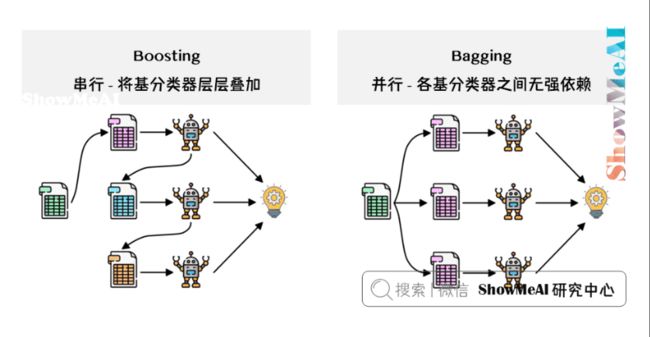
Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。
Bagging 与 Boosting 的串行训练方式不同,Bagging方法在训练过程中,各基分类器之间无强依赖,可以进行并行训练。
GBDT详解
GBDT的原理
(1)所有弱分类器的结果相加等于预测值;
(2)每次都以当前预测为基准,下一个弱分类器去拟合误差函数对预测值的残差(预测值与真实值之间的误差)
(3)GBDT的弱分类器使用的是树模型
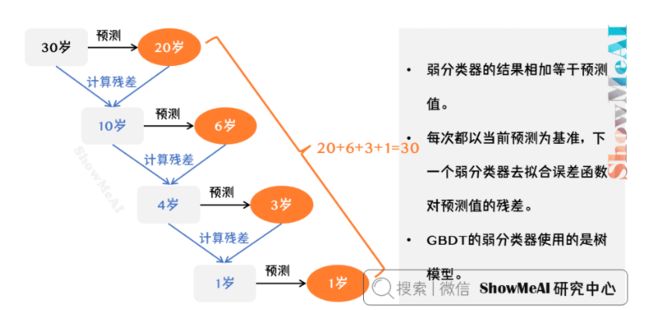
如下图所示是一个非常简单的帮助理解的示例,我们用GBDT去预测年龄:
第一个弱分类器(第一棵树)预测一个年龄(如20岁),计算发现误差有10岁;
第二棵树预测拟合残差,预测值6,计算发现差距还有4岁;
第三棵树继续预测拟合残差,预测值3,发现差距只有1岁了;
第四课树用1岁拟合剩下的残差,完成。
最终,四棵树的结论加起来,得到30岁这个标注答案(实际工程实现里,GBDT是计算负梯度,用负梯度近似残差)。
GBDT与负梯度近似残差
回归任务下,GBDT在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数:
l ( y i , y i ^ ) = 1 2 ( y i − y i ^ ) 2 l(y_i,\hat{y_i})=\frac{1}{2}(y_i-\hat{y_i})^2 l(yi,yi^)=21(yi−yi^)2
损失函数的负梯度计算如下:
− [ ∂ l ( y i , y i ^ ) ∂ y i ^ ] = ( y i − y i ^ ) -[\frac{\partial l(y_i,\hat{y_i})}{\partial\hat{y_i}}]=(y_i-\hat{y_i}) −[∂yi^∂l(yi,yi^)]=(yi−yi^)
可以看出,当损失函数选用**「均方误差损失」时,每一次拟合的值就是(真实值-预测值),即残差。**
GBDT训练过程
我们来借助1个简单的例子理解一下 GBDT 的训练过程。
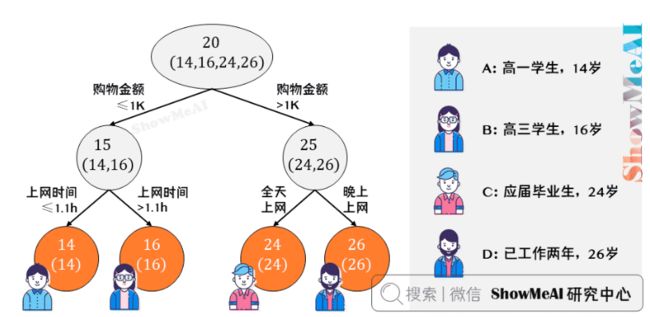
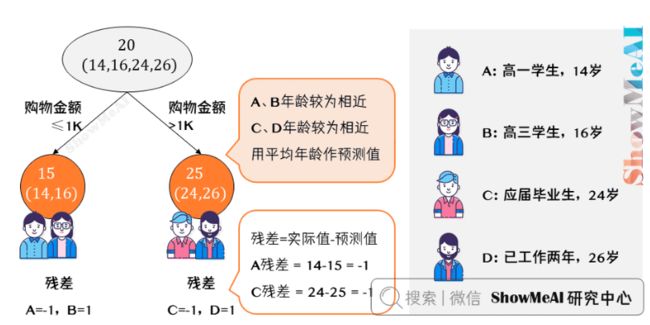
假设训练集只有4个人(A,B,C,D),他们的年龄分别为(14,16,24,26)。其中,A,B分别是高一和高三学生;C和D分别是应届毕业生和工作两年的员工。
我们先看看用回归树来训练,得到的结果如下图所示:
接下来改用 GBDT来训练。由于样本数据少,我们限定叶子节点最多为2(及每棵树都只有一个分支),并且限定树的棵树为2,最终训练得到的结果如下图所示:
上图中的树很好理解:A,B年龄较为相近,C,D年龄较为相近,被分为左右两支,每支用平均年龄作为预测值。
我们计算残差(即「实际值」-「预测值」),所以A的残差为:14-15=-1
这里A的「预测值」是指前面所有树预测结果累加的和,在当前情形下前序只有一棵树,所以直接是15,其他多树的复杂场景下需要累加计算作为A的预测值。
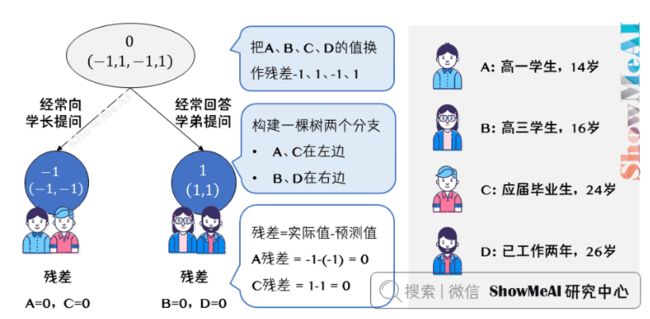
上图中的树就是残差学习的过程了:
把A,B,C,D的值换作残差-1、1、-1、1,再构建一棵树学习,这棵树只有两个值1和-1,直接分成两个节点:A、C在左边,B、D在右边。
这棵树学习残差,在我们当前这个简单的场景下,已经能保证预测值和实际值(上一轮残差)相等了。
我们把这棵树的预测值累加到第一棵树上的预测结果上,就能得到真实年龄,这个简单例子中每个人都完美匹配,得到了真实的预测值。
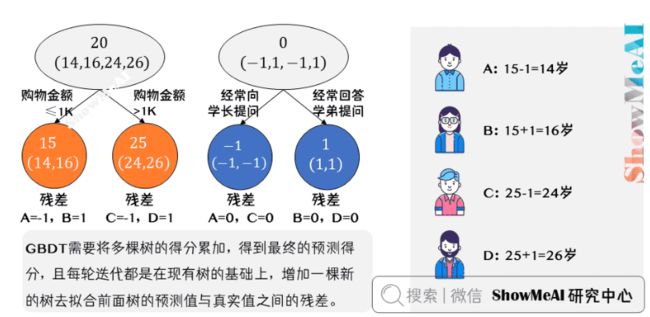
最终的预测过程是这样的:
1)A:高一学生,购物较少,经常问学长问题,真实年龄14岁,预测年龄A=15-1=14
2)B:高三学生,购物较少,经常被学弟提问,真实年龄16岁,预测年龄B=15+1=16
3)C:应届毕业生,购物较多,经常问学长问题,真实年龄24岁,预测年龄C=25-1=24
4)D:工作两年员工,购物较多,经常被学弟提问,真实年龄26岁,预测年龄D=25+1=26
综上,GBDT需要将多棵树的得分累加得到最终的预测得分,且每轮迭代,都是在现有树的基础上,增加一棵新的树去拟合前面树的预测值与真实值之间的残差。
梯度提升 vs 梯度下降
下面我们来对比一下「梯度提升」与「梯度下降」。这两种迭代优化算法,都是在每1轮迭代中,利用损失函数负梯度方向的信息,更新当前模型,只不过:
梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参数的更新。
F = F T − 1 − ρ t ∇ F L ∣ F = F t − 1 L = ∑ i l ( y i , F ( x i ) ) \begin{split} &F=F_{T-1}-\rho_t\nabla_FL|_{F=F_{t-1}}\\ &L=\sum_{i}l(y_i,F(x_i)) \end{split} F=FT−1−ρt∇FL∣F=Ft−1L=i∑l(yi,F(xi))
梯度提升中,模型并不需要进行参数化表示,而是直接定义在函数空间中,从而大大扩展了可以使用的模型种类。
ω t = ω t − 1 − ρ t ∇ ω L ∣ ω = ω t − 1 L = ∑ i l ( y i , f ω ( ω i ) ) \begin{split} &\omega_t=\omega_{t-1}-\rho_t\nabla_{\omega}L|_{\omega=\omega_{t-1}}\\ &L=\sum_{i}l(y_i,f_{\omega}(\omega_i)) \end{split} ωt=ωt−1−ρt∇ωL∣ω=ωt−1L=i∑l(yi,fω(ωi))
GBDT优缺点
下面我们来总结一下 GBDT 模型的优缺点:
优点
预测阶段,因为每棵树的结构都已确定,可并行化计算,计算速度快。
适用稠密数据,泛化能力和表达能力都不错,数据科学竞赛榜首常见模型。
可解释性不错,鲁棒性亦可,能够自动发现特征间的高阶关系。
缺点
1)GBDT 在高维稀疏的数据集上,效率较差,且效果表现不如 SVM 或神经网络。
2)适合数值型特征,在 NLP 或文本特征上表现弱。
3)训练过程无法并行,工程加速只能体现在单颗树构建过程中。
随机森林 vs GBDT
相同点
1)都是集成模型,由多棵树组构成,最终的结果都是由多棵树一起决定。
2)RF 和 GBDT 在使用 CART 树时,可以是分类树或者回归树。
不同点
1)训练过程中,随机森林的树可以并行生成,而 GBDT 只能串行生成。
2)随机森林的结果是多数表决表决的,而 GBDT 则是多棵树累加之。
3)随机森林对异常值不敏感,而 GBDT 对异常值比较敏感。
4)随机森林降低模型的方差,而 GBDT 是降低模型的偏差。
可以是分类树或者回归树。
不同点
1)训练过程中,随机森林的树可以并行生成,而 GBDT 只能串行生成。
2)随机森林的结果是多数表决表决的,而 GBDT 则是多棵树累加之。
3)随机森林对异常值不敏感,而 GBDT 对异常值比较敏感。
4)随机森林降低模型的方差,而 GBDT 是降低模型的偏差。