LL(1)分析法(一) ——文法预处理以及FIRST集FOLLOW集求解(编译原理)
LL(1)分析法
预期达到目标
- 对给定文法,求出各个非终结符的FIRST集,FOLLOW集
- 根据给定文法建立LL(1)分析表
- 对输入的表达式符号串能够给出分析过程输出分析结果
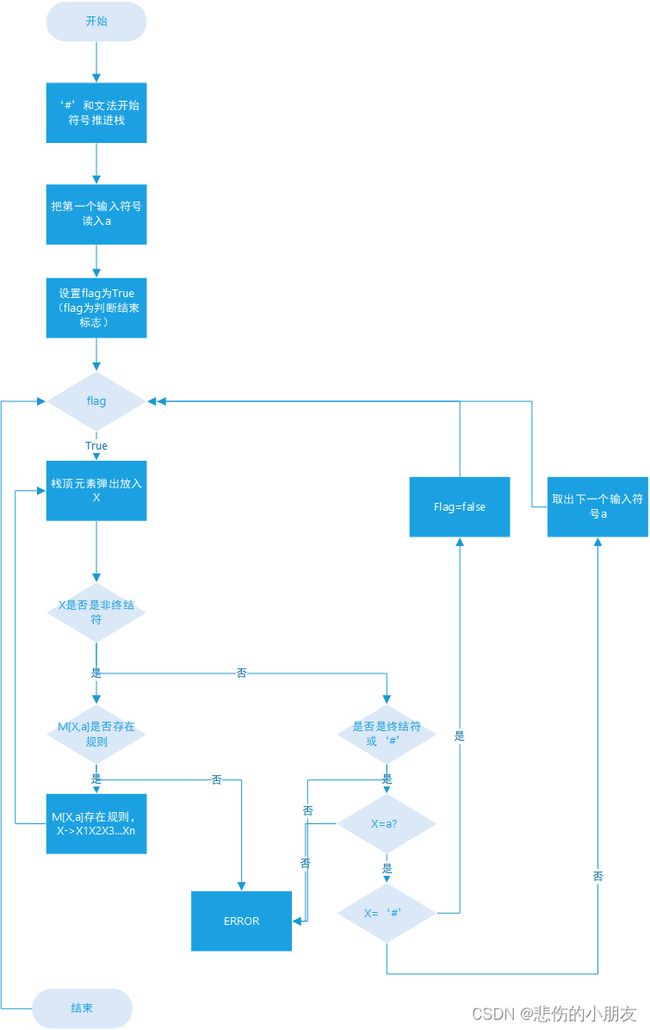
LL(1)预测分析程序整体流程
一些初始设定
name_source = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N',
'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
op = ['(', ')', '{', '}', '[', ']', '/', '\\', '*', '+', '!', '-', '%', '>', '<', '='] #能够识别的一些除小写字母以外的非终结符(操作符)
数据结构设计
实现代码:
class Infinite:
def __init__(self, name):
self.name = name
self.equalList = []
self.FIRST = set()
self.FOLLOW = set()
def equalList_change(self, express):
expresses = express.split('|')
for express in expresses:
self.equalList.append(express)
# 将输入文法转换为LL(1)文法
对输入文法读取以及初始化
代码:
def init(expresses):
infinite = {}
name_get = name_source
for express in expresses:
name = express[0]
equal = express[3:]
if name not in infinite.keys():
inf = Infinite(name)
infinite[name] = inf
name_get.remove(name)
else:
inf = infinite[name]
inf.equalList_change(equal)
print("输入的文法:")
for name in infinite.keys():
print(name, end="->")
s = '|'.join(infinite[name].equalList)
print(s)
return infinite, name_get
文法预处理
- 判定输入文法是否为LL(1)文法,若不是则通过变化将其转换为LL(1)文法
- 根据转换后的等价正规文法建立非终结符的映射关系
LL(1)文法判定与转换
LL(1)文法有三个条件:
- LL(1)文法不含左递归
- 文法中每个非终结符的FIRST集两两不相交。
- 当一个文法的FIRST集内含空串时,其FIRST集与FOLLOW集不能相交。
考虑到以上三个条件,对于输入文法,我们首先需要通过简要判断是否存在左递归,若存在左递归则需要进行消除。对于避免FIRST集相交,需要通过提取公共左因子。在进行完上述操作后再进行验证是否满足文法条件。
文法内容读取
采用正则表达式进行文法匹配,并判定文法中是否存在不匹配项(无效式)
注意此处你的文本文件的保存编码类型,当然如果你选择使用文本文件保存就要注意,最好加个编码方式
def expressGet(fileName):
with open(fileName, 'r',encoding='utf-8') as f:
express = f.read()
regex = "[A-Z]->[a-zA-Z|*+-/(){}ε]+"
res = re.findall(regex, express)
if len(res) == len(express.split('\n')):
return res # 说明输入的文法合法,否则说明输入的文法中有不匹配项
文法左递归消除
左递归分为两种分别为直接左递归和间接左递归。对于间接左递归通常是通过将其转化为直接左递归后然后进行消除。

当然大家看到这里一定很迷,我第一次看到也是这样想的,那么这个应该怎么实现呢?下面请看代码
实现代码
def removeLeft(expresses):
"""
消除左递归
:param expresses: 输入产生式
:return:新的消除左递归后的文法
"""
infinite, name_get = init(expresses)
name_list = list(infinite.keys())
for i in range(0, len(name_list)):
infinite_i = infinite[name_list[i]]
for j in range(0, i):
infinite_j = infinite[name_list[j]]
for equal in infinite_i.equalList:
if equal[0] == infinite_j.name:
if len(equal)>1:
for j_equal in infinite_j.equalList:
new_equal = j_equal + equal[1:]
infinite_i.equalList.append(new_equal)
infinite_i.equalList.remove(equal)
new_name = name_get[0] # 添加新非终结符
target = []
flag = False
for k in range(len(infinite_i.equalList)):
if infinite_i.equalList[k][0] == infinite_i.name: # 消除直接左递归
flag = True
for j in range(0, len(infinite_i.equalList)):
if infinite_i.equalList[j][0] != infinite_i.name:
"""对于不是左递归的后加符号"""
infinite_i.equalList[j] += new_name
target.append(infinite_i.equalList[k])
infinite_i.equalList.remove(infinite_i.equalList[k]) # 删除左递归
if flag:
infinite_new = Infinite(new_name)
for equ in target:
equ_temp = equ[1:] + new_name
infinite_new.equalList.append(equ_temp)
infinite_new.equalList.append('ε')
infinite[new_name] = infinite_new
name_get.remove(new_name)
print("消除左递归后的文法:")
for name in infinite.keys():
print(name,end="->")
s = '|'.join(infinite[name].equalList)
print(s)
leftGet(infinite, name_get)
FIRST_get(infinite)
FOLLOW_get(infinite)
结果展示
消除左递归算法其实只是看起来复杂,但实际上也只是个纸老虎,只要照着算法的具体流程来,我相信懂得基本for循环以及if判断语句的人应该都能够实现,因此此处我不再对具体细节进行过多解释,如果有疑问对流程不理解,建议手动模拟一下操作流程来加深对算法的理解。
文法公共左因子提取
在消除左递归后,对于文法中出现的公共左因子进行提取,以避免出现FIRST相交
实现代码:
def leftGet(infinite, name_get):
name_list = list(infinite.keys())
for name in name_list:
first_set = set()
for equal in infinite[name].equalList:
first_set.add(equal[0])
for first in first_set:
same_equal = [equal for equal in infinite[name].equalList if equal[0] == first]
if len(same_equal) >1:
"""说明存在公共左因子,则采取提取公共左因子操作"""
new_name = name_get[0]
new_infinite = Infinite(new_name)
name_get.remove(new_name)
same = same_equal[0][0]
for equ in same_equal:
new_infinite.equalList.append(equ[1:])
infinite[name].equalList.remove(equ)
infinite[name].equalList.append(same+new_name)
infinite[new_name] = new_infinite
for name in infinite.keys():
print(name,end="->")
s = '|'.join(infinite[name].equalList)
print(s)
这部分内容属于看着难,但真正进行实现的时候并没遇到特别多的困难。
文法FIRST集与FOLLOW集求解
FIRST集求解
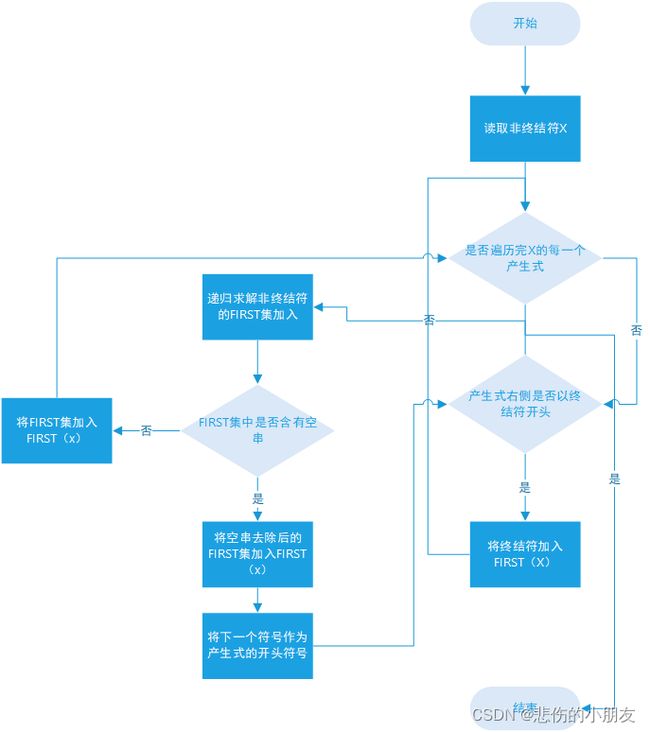
求解算法概述
算法思路分析与代码实现
此处对于终结符的FIRST集的求解我觉得不需要再考虑,主要是对于非终结符的FIRST集。
仔细分析算法思路发现算法的实现应该是通过递归来进行的,在求解一个FIRST集时若遇到以非终结符开头的则需要递归求解该非终结符的FIRST集。
算法流程图:
实现代码:
def FIRST_next(infinite, name, get_record):
"""
求解FIRST集使用的递归函数
:param infinite: 终结符字典
:param name: 要求解的终结符
:param get_record: 记录是否已经求解过
:return: None
"""
if get_record[name]:
return
for equal in infinite[name].equalList:
if equal[0].islower():
infinite[name].FIRST.add(equal[0])
elif equal == 'ε':
infinite[name].FIRST.add(equal)
else:
if not get_record[equal[0]]: # 没有求解则需要递归求解
FIRST_next(infinite, equal[0], get_record)
# 判断是否含有空串
if 'ε' in infinite[equal[0]].FIRST: # 含有时则需要去除空串
new_set = set(infinite[equal[0]].FIRST)
new_set.discard('ε')
infinite[name].FIRST=infinite[name].FIRST.union(new_set)
for new_name in equal[1:]:
if new_name.islower():
infinite[name].FIRST.add(new_name)
break
else:
FIRST_next(infinite, new_name, get_record)
if 'ε' not in infinite[equal[0]].FIRST:
new1_set = set(infinite[equal[0]].FIRST)
infinite[name].FIRST=infinite[name].FIRST.union(new1_set)
break
else:
new1_set = set(infinite[equal[0]].FIRST)
new1_set.discard('ε')
infinite[name].FIRST=infinite[name].FIRST.union(new1_set)
continue
else:
new_set = set(infinite[equal[0]].FIRST)
infinite[name].FIRST=infinite[name].FIRST.union(new_set)
get_record[name] = True
def FIRST_get(infinite):
"""
求解FIRST集
:param infinite:
:return:返回更新后的字典
"""
get_record = {} # 用来记录那些非终结符的FIRST集已经被求解
name_list = list(infinite.keys())
for name in name_list:
get_record[name] = False
for name in name_list:
FIRST_next(infinite, name, get_record)
for name in name_list:
print(name, end=":")
print(infinite[name].FIRST)
改进
其实这样已经能够求解出FIRST集,这部分任务应该可以到此为止了,但是由于后面要建立LL(1)分析表,因此仅仅求出FIRST集是远远不够的,还要记录FIRST集中的每一个元素与产生式间的对应关系
改进的代码
def FIRST_next(infinite, name, get_record):
"""
求解FIRST集使用的递归函数
:param infinite: 终结符字典
:param name: 要求解的终结符
:param get_record: 记录是否已经求解过
:return: None
"""
if get_record[name]:
return
for equal in infinite[name].equalList:
if equal[0].islower() or equal[0] in op:
infinite[name].FIRST.setdefault(equal[0], [])
infinite[name].FIRST[equal[0]].append(equal)
elif equal == 'ε':
infinite[name].FIRST.setdefault(equal, [])
infinite[name].FIRST['ε'].append(equal)
else:
if not get_record[equal[0]]: # 没有求解则需要递归求解
FIRST_next(infinite, equal[0], get_record)
# 判断是否含有空串
if 'ε' in infinite[equal[0]].FIRST: # 含有时则需要去除空串
new_set = set(infinite[equal[0]].FIRST)
new_set.discard('ε')
# infinite[name].FIRST=infinite[name].FIRST.union(new_set)
for key in infinite[equal[0]].FIRST.keys():
infinite[name].FIRST.setdefault(key, [])
infinite[name].FIRST[key].append(equal)
for new_name in equal[1:]:
if new_name.islower() or equal[0] in op:
infinite[name].FIRST.setdefault(new_name, [])
infinite[name].FIRST[new_name].append(equal)
break
else:
FIRST_next(infinite, new_name, get_record)
if 'ε' not in infinite[equal[0]].FIRST:
for key in infinite[equal[0]].FIRST.keys():
infinite[name].FIRST.setdefault(key, [])
infinite[name].FIRST[key].append(equal)
break
else:
new1_set = set(infinite[equal[0]].FIRST)
new1_set.discard('ε')
for key in new1_set:
infinite[name].FIRST.setdefault(key, [])
infinite[name].FIRST[key].append(equal)
continue
else:
for key in infinite[equal[0]].FIRST.keys():
infinite[name].FIRST.setdefault(key, [])
infinite[name].FIRST[key].append(equal)
get_record[name] = True
def FIRST_get(infinite):
"""
求解FIRST集
:param infinite:
:return:返回更新后的字典
"""
get_record = {} # 用来记录那些非终结符的FIRST集已经被求解
name_list = list(infinite.keys())
for name in name_list:
get_record[name] = False
for name in name_list:
FIRST_next(infinite, name, get_record)
print("各个非终结符的FIRST集:")
for name in name_list:
print(name, end=":")
print(infinite[name].FIRST)


这样就可以通过FIRST集判断用户输入的文法是否符合LL(1)文法要求
编写代码的难度还是有的但相比与一些算法竞赛题,难度还是小了不少,而且思路也相对清晰,大家可以对着敲一下试试,我相信只要不是复制粘贴,大家在这个过程中应该会很清晰我的思路
FOLLOW集求解
FOLLOW(A)是所有句型中出现的在紧接A之后的终结符或‘#’

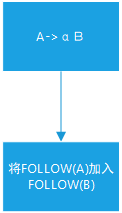
求解算法概述
算法思路分析与代码实现
这个算法的描述也很抽象,自己就很难理解整个求解过程,更不用说还要编写计算机程序,来求解了。哎但怎么说呢,如果不动手尝试一下,又怎么知道自己就一定不可以呢?
FIRST集求解其思路本质上是从产生式的左侧根据产生式的右侧来求解,而FOLLOW集的求解从我给出的算法描述上看,就应该能看出其实分析产生式的右侧来推算FOLLOW集的。
此处默认以文法的第一个符号为开始符号,后面在进行系统设计时可通过增加接口来供用户自定义开始符号,并且此处算法要注意别有一个坑,就是要求解的FOLLOW的目标非终结符其产生式的末尾恰好以其自身为结尾要注意这种情况的判断以及去除避免陷入死循环(算法看起来没有提及这一点但好像就我一个人不知道)
算法流程图:

实现代码:
def FOLLOW_next(infinite, name, get_record, name_list):
if get_record[name]: # 已被求结果则直接返回
return
for find_name in name_list:
for equal in infinite[find_name].equalList:
if name in equal: # 要求解的非终结符在产生式中
index = equal.index(name)
if index == len(equal) - 1 and find_name != name: # 在末尾位置
FOLLOW_next(infinite, find_name, get_record, name_list) # 递归调用求解FOLLOW集
infinite[name].FOLLOW = infinite[name].FOLLOW.union(infinite[find_name].FOLLOW)
elif index < len(equal) - 1 and (equal[index + 1].islower() or equal[index + 1] in op): # 紧接着的为终结符
infinite[name].FOLLOW.add(equal[index + 1])
else: # 紧接着的是非终结符
if index < len(equal) - 1:
if 'ε' not in set(infinite[equal[index + 1]].FIRST.keys()):
keys = set(infinite[equal[index + 1]].FIRST.keys())
for key in keys:
infinite[name].FOLLOW.add(key)
else: # 空串在内的情况
pos = index + 1
first = list(infinite[equal[pos]].FIRST.keys()) # 存储first集合
while 'ε' in first:
first.remove('ε')
for key in first:
infinite[name].FOLLOW.add(key)
if equal[pos].islower() or equal[pos] in op:
infinite[name].FOLLOW.add(equal[pos])
break
if pos + 1 >= len(equal):
break
else:
pos += 1
first = list(infinite[equal[pos]].FIRST.keys())
if pos + 1 == len(equal):
first = list(infinite[equal[pos]].FIRST.keys())
if 'ε' in first:
FOLLOW_next(infinite, find_name, get_record, name_list) # 递归调用求解FOLLOW集
infinite[name].FOLLOW = infinite[name].FOLLOW.union(infinite[find_name].FOLLOW)
get_record[name] = True
def FOLLOW_get(infinite, start=0):
get_record = {}
name_list = list(infinite.keys())
for name in name_list:
get_record[name] = False
if start == 0: # 说明没有自定义开始符号,默认以第一个符号为开始符号
infinite[name_list[0]].FOLLOW.add('#')
for name in name_list:
FOLLOW_next(infinite, name, get_record, name_list)
print("各个非终结符的FOLLOW集:")
for name in name_list:
print(name, end=":")
print(infinite[name].FOLLOW)
到此对于文法的初步处理已经全部完成,回顾上面我们进行了消除左递归,提取公共左因子,求解FIRST集和FOLLOW集。这个过程确实很痛苦,在我没有动手开始实现的时候,我甚至不相信自己能够完成这个艰难的过程。但我最终还是实现了,尽管过程中遇到了很多很多的困难,进行了很多很多的调试,反复测试代码思考逻辑问题,过程很艰难但现在还是蛮有成就感的。下面便是根据LL(1)分析表开始着手进行语法分析,继续加油!!!!
这里我把目前的代码截图贴出来,但不能贴源码,因为毕竟实验还未验收,而且我希望大家能够自己实现一下,如果需要源码请私聊
原先是想在一篇文章实现整个分析过程的,但考虑到内容实在太多因此决定下面在下一篇文章中继续讲解,还望大家持续关注~~~~