CRC计算模型
Poly 生成多项式
Init CRC初始值
RefIn 指的就是如果这个值是FALSE,表示待测数据的每个字节都不用“颠倒”,即BIT7仍是作为最高位,BIT0作为最低位。如果这个值是TURE,表示待测数据的每个字节都要先“颠倒”,即BIT7作为最低位,BIT0作为最高位。
RefOut 是说如果这个值是FALSE,表示计算结束后,寄存器中的值直接进入XOROUT处理即可,如果这个值是TURE,表示计算结束后,寄存器中的值要先“颠倒”,再进入XOROUT处理。注意,这是将整个寄存器的值颠倒,由最高bit到最低bit进行颠倒。
XorOut 这个值与经RefOut后的寄存器的值相XOR,得到的值就是最终正式的CRC值!
CRC计算的详细公式见《CRC校验算法原理及实现》一文:crc校验算法原理及实现
按位计算 CRC
计算本位后的CRC码等于((上一位CRC码乘以2后除以多项式,所得的余数)再加上(本位值左移WIDTH(16)位后除以多项式所得的余数)。
采用CRC-CCITT多项式,多项式为0x11021,C语言编程时,参与计算为0x1021,这个地方得深入思考才能体会其中的奥妙,分享一下我的思路:当按位计算CRC时,例如计算二进制序列为1001 1010 1010 1111时,将二进制序列数左移16位,即为1001 1010 1010 1111 (0000 0000 0000 0000),实际上该二进制序列可拆分为1000 0000 0000 0000 (0000 0000 0000 0000) + 000 0000 0000 0000 (0000 0000 0000 0000) + 00 0000 0000 0000 (0000 0000 0000 0000) + 1 0000 0000 0000 (0000 0000 0000 0000) + ……
现在开始分析运算:
<1>对第一个二进制分序列求余数,竖式除法即为0x10000 ^ 0x11021运算,后面的0位保留;
<2>接着对第二个二进制分序列求余数,将第一步运算的余数*2后再和第二个二进制分序列一起对0x11021求余,这一步理解应该没什么问题。如果该分序列为0,无需计算。
<3>对其余的二进制序列求余与上面两步相同。
<4>计算到最后一位时即为整个二进制序列的余数,即为CRC校验码。
该计算方法相当于对每一位计算,运算过程很容易理解,所占内存少,缺点是一位一位计算比较耗时
下面给出C语言实现方法:
*ptr指向发送缓冲区的首字节,crc_init是crc计算初始值,len是要发送的总字节数
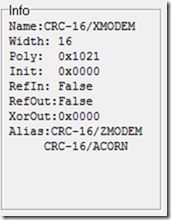
//Name: CRC-16/XMODEM //Width: 16 //Poly: 0x1021 //Init: 0x0000 //RefIn: False //RefOut:False //XorOut: 0x0000 //Alias:CRC-16/ZMODEM // CRC-16/ACORN unsigned int cal_crc(unsigned char *ptr, unsigned char len) { unsigned int crc_init=0x0000; unsigned int crc=crc_init; ungigned int i; while(len--) { for(i=0x80; i!=0; i>>=1) { crc<<=1; //crc left shift 1bit crc*2 if((crc&0x10000)!=0) { crc^=0x11021; } If((*ptr&i)!=0) { crc=crc^(0x10000^0x11021); } } ptr++; } return crc; }
上面的程序根据运算分析而来,很容易理解。为了节约内存空间,我们对程序作进一步的简化。分析可知,当二进制序列中上一位计算的余数第15bit位为1时,即( 上一位计算的余数 & 0x8000) != 0,计算本位时,上一位余数 * 2后可对0x11021作求余运算,然后再加上本位计算所得余数。这个很好理解,也就是说,打个比方,把它看作简单的除法,计算上一位时的余数乘以2后,如果比较大可以当被除数,就再去除除数求余。有一点和普通除法不同的是,因为多项式除法中采用不带借位的减法运算,所以0x10000也可以被0x11021除,余数并非为0x10000,而是0x1021。这个自己动手算一下就知道了。余数之和也是不带进位的加法运算,即异或。最后还强调一点,因为二进制序列是左移16位后参与运算的,所以,一直算到序列的最后一位也是可以被除的,这点大家要明白。下面给出简化后的C语言实现。
//Name: CRC-16/XMODEM //Width: 16 //Poly: 0x1021 //Init: 0x0000 //RefIn: False //RefOut:False //XorOut: 0x0000 //Alias:CRC-16/ZMODEM // CRC-16/ACORN unsigned int cal_crc(unsigned char *ptr, unsigned char len) { unsigned int crc_init=0x0000; unsigned int crc=crc_init; ungigned int i; while(len--) { for(i=0x80; i!=0; i>>=1) { if(crc&0x8000)!=0) { crc<<=1; //crc left shift 1bit crc*2 crc^=0x1021; } else { crc<<=1; //crc left shift 1bit crc*2 } If((*ptr&i)!=0) { crc^=0x1021; } } ptr++; } return crc; }
因为0x1021^0x1021=0,而当两个if条件都成立或都不成立时,crc值不变,而当两个if条件有一个成立时,crc^=0x1021,所以上述代码可以修改为:
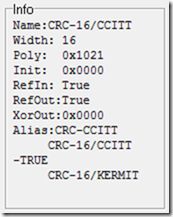
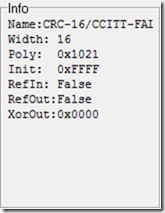
//Name: CRC-16/XMODEM //Width: 16 //Poly: 0x1021 //Init: 0x0000 //RefIn: False //RefOut:False //XorOut: 0x0000 //Alias:CRC-16/ZMODEM // CRC-16/ACORN unsigned int cal_crc(unsigned char *ptr, unsigned char len) { unsigned int crc_init=0x0000; unsigned int crc=crc_init; unsigned int temp; ungigned int i; while(len--) { for(i=0; i<8; i++) { temp=((*ptr<<i)&0x80)^((crc&0x80000)>>8); crc<<=1; //crc left shift 1bit crc*2 If(temp!=0) { crc^=0x1021; } } ptr++; } return crc; } //Name: CRC-16/CCITT-FALSE //Width: 16 //Poly: 0x1021 //Init: 0xFFFF //RefIn: False //RefOut:False //XorOut: 0x0000 unsigned int cal_crc(unsigned char *ptr, unsigned char len) { unsigned int crc_init=0xFFFF; unsigned int crc=crc_init; ungigned int i; while(len--) { for(i=0x80; i!=0; i>>=1) { if(crc&0x8000)!=0) { crc<<=1; //crc left shift 1bit crc*2 crc^=0x1021; } else { crc<<=1; //crc left shift 1bit crc*2 } If((*ptr&i)!=0) { crc^=0x1021; } } ptr++; } return crc; } //Name: CRC-16/CCITT //Width: 16 //Poly: 0x1021 //Init: 0x0000 //RefIn: Ture //RefOut: Ture //XorOut: 0x0000 //Alias:CRC-CCITT // CRC-16/CCITT //-TRUE // CRC-16/KERMIT unsigned int cal_crc(unsigned char *ptr, unsigned char len) { unsigned int crc_init=0x0000; unsigned int crc=crc_init; unsigned int temp; unsigned int crc_temp; ungigned int i; while(len--) { for(i=8; i>0; i--) { temp=((*ptr<<i)&0x80)^((crc&0x80000)>>8); crc<<=1; //crc left shift 1bit crc*2 If(temp!=0) { crc^=0x1021; } } ptr++; } for(i=0;i<8;i++) { crc_temp|=((((0x8000>>i)&crc)>>(15-i))|(((0x0001<<i)&crc)<<(15-i))); } crc=crc_temp; return crc; }
按字节计算CRC
计算本字节后的 CRC 码等于((上一字节余式CRC 码的低 8 位左移 8位后),再加上((上一字节 CRC 右移 8 位(也既取高 8 位)和本字节之和)左移16位))后所求得的CRC码。
有了上面按位计算的知识,理解这个就是小case了。还是举前面的例子:当字节计算CRC时,例如计算二进制序列为1001 1010 1010 1111时,即0x9a9f时,将二进制序列数左移16位,即为0x9a9f(0 0 0 0),实际上该二进制序列可拆分为0x9a00(0 0 0 0) + 0x009f(0 0 0 0),分析计算时和上面的步骤一样,唯一不同的是计算中上一步的余数CRC要乘以2的八次方参与下一步的运算,这个应该好理解撒。为了简化编程,将计算中的CRC拆成高八位和低八位的形式,高八位的值直接与本位值相加求余,(低八位的值乘以2的八次方后作为余数)和计算得的余数相加。为了提高计算速度,我们把8位二进制序列数的CRC全部计算出来,放在一个表中,采用查表法可大大提高计算速度。
//Name: CRC-16/XMODEM //Width: 16 //Poly: 0x1021 //Init: 0x0000 //RefIn: False //RefOut:False //XorOut: 0x0000 //Alias:CRC-16/ZMODEM // CRC-16/ACORN unsigned int crc_table[256] ={ 0x0000, 0x1021, 0x2042, 0x3063, 0x4084, 0x50a5, 0x60c6, 0x70e7, 0x8108, 0x9129, 0xa14a, 0xb16b, 0xc18c, 0xd1ad, 0xe1ce, 0xf1ef, 0x1231, 0x0210, 0x3273, 0x2252, 0x52b5, 0x4294, 0x72f7, 0x62d6, 0x9339, 0x8318, 0xb37b, 0xa35a, 0xd3bd, 0xc39c, 0xf3ff, 0xe3de, 0x2462, 0x3443, 0x0420, 0x1401, 0x64e6, 0x74c7, 0x44a4, 0x5485, 0xa56a, 0xb54b, 0x8528, 0x9509, 0xe5ee, 0xf5cf, 0xc5ac, 0xd58d, 0x3653, 0x2672, 0x1611, 0x0630, 0x76d7, 0x66f6, 0x5695, 0x46b4, 0xb75b, 0xa77a, 0x9719, 0x8738, 0xf7df, 0xe7fe, 0xd79d, 0xc7bc, 0x48c4, 0x58e5, 0x6886, 0x78a7, 0x0840, 0x1861, 0x2802, 0x3823, 0xc9cc, 0xd9ed, 0xe98e, 0xf9af, 0x8948, 0x9969, 0xa90a, 0xb92b, 0x5af5, 0x4ad4, 0x7ab7, 0x6a96, 0x1a71, 0x0a50, 0x3a33, 0x2a12, 0xdbfd, 0xcbdc, 0xfbbf, 0xeb9e, 0x9b79, 0x8b58, 0xbb3b, 0xab1a, 0x6ca6, 0x7c87, 0x4ce4, 0x5cc5, 0x2c22, 0x3c03, 0x0c60, 0x1c41, 0xedae, 0xfd8f, 0xcdec, 0xddcd, 0xad2a, 0xbd0b, 0x8d68, 0x9d49, 0x7e97, 0x6eb6, 0x5ed5, 0x4ef4, 0x3e13, 0x2e32, 0x1e51, 0x0e70, 0xff9f, 0xefbe, 0xdfdd, 0xcffc, 0xbf1b, 0xaf3a, 0x9f59, 0x8f78, 0x9188, 0x81a9, 0xb1ca, 0xa1eb, 0xd10c, 0xc12d, 0xf14e, 0xe16f, 0x1080, 0x00a1, 0x30c2, 0x20e3, 0x5004, 0x4025, 0x7046, 0x6067, 0x83b9, 0x9398, 0xa3fb, 0xb3da, 0xc33d, 0xd31c, 0xe37f, 0xf35e, 0x02b1, 0x1290, 0x22f3, 0x32d2, 0x4235, 0x5214, 0x6277, 0x7256, 0xb5ea, 0xa5cb, 0x95a8, 0x8589, 0xf56e, 0xe54f, 0xd52c, 0xc50d, 0x34e2, 0x24c3, 0x14a0, 0x0481, 0x7466, 0x6447, 0x5424, 0x4405, 0xa7db, 0xb7fa, 0x8799, 0x97b8, 0xe75f, 0xf77e, 0xc71d, 0xd73c, 0x26d3, 0x36f2, 0x0691, 0x16b0, 0x6657, 0x7676, 0x4615, 0x5634, 0xd94c, 0xc96d, 0xf90e, 0xe92f, 0x99c8, 0x89e9, 0xb98a, 0xa9ab, 0x5844, 0x4865, 0x7806, 0x6827, 0x18c0, 0x08e1, 0x3882, 0x28a3, 0xcb7d, 0xdb5c, 0xeb3f, 0xfb1e, 0x8bf9, 0x9bd8, 0xabbb, 0xbb9a, 0x4a75, 0x5a54, 0x6a37, 0x7a16, 0x0af1, 0x1ad0, 0x2ab3, 0x3a92, 0xfd2e, 0xed0f, 0xdd6c, 0xcd4d, 0xbdaa, 0xad8b, 0x9de8, 0x8dc9, 0x7c26, 0x6c07, 0x5c64, 0x4c45, 0x3ca2, 0x2c83, 0x1ce0, 0x0cc1, 0xef1f, 0xff3e, 0xcf5d, 0xdf7c, 0xaf9b, 0xbfba, 0x8fd9, 0x9ff8, 0x6e17, 0x7e36, 0x4e55, 0x5e74, 0x2e93, 0x3eb2, 0x0ed1, 0x1ef0}; unsigned int cal_crc(unsigned char *ptr, unsigned char len) { unsigned int crc_init=0x0000; unsigned int crc=crc_init; unsigned char crc_H8; while(len--) { crc_H8=(unsigned char) (crc>>8); crc<<=8; crc^=crc_table[crc_H8^ *ptr]; ptr++; } return crc; }
按半字节计算 CRC
计算本字节后的 CRC 码等于((上一字节 CRC 码的低 12 位左移 4 位后),再加上(((上一字节余式 CRC 右移12 位(也既取高 4 位))和本字节之和)左移16位))后所求得的 CRC 码。
如果我们把 4 位二进制序列数的 CRC 全部计算出来,放在一个表里,采用查表法, 每个字节算两次(半字节算一次),可以在速度和内存空间取得均衡。
//Name: CRC-16/XMODEM //Width: 16 //Poly: 0x1021 //Init: 0x0000 //RefIn: False //RefOut:False //XorOut: 0x0000 //Alias:CRC-16/ZMODEM // CRC-16/ACORN unsigned int crc_table[16] =={0x0000, 0x1021, 0x2042, 0x3063, 0x4084, 0x50a5, 0x60c6, 0x70e7, 0x8108, 0x9129, 0xa14a, 0xb16b, 0xc18c, 0xd1ad, 0xe1ce, 0xf1ef=}; unsigned int cal_crc(unsigned char *ptr, unsigned char len) { unsigned int crc_init=0x0000; unsigned int crc=crc_init; unsigned char crc_H4; while(len--) { crc_H4=(unsigned char) (crc>>12); //high 4 bits crc<<=4; //LOW 12 BITS crc^=crc_table[crc_H4^(*ptr>>4)]; //(crc high 4bits plus high 4)calculate crc ,then plus // crc of last crc crc_H4=(unsigned char) (crc>>12); crc<<=4; crc^=crc_table[crc_H4^(*ptr&0x0f)]; //(crc high 4bits plus low 4)calculate crc,then plus //crc of last crc ptr++; } return crc; }