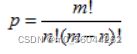C语言经典算法
目录
一、冒泡排序
二、斐波那契函数问题
1、普通解法
2、用数组实现斐波那契函数
三、猴子吃桃问题
四、素数问题
五、最大公约数与最小公倍数
1、使用for循环实现
2、使用辗转相除法
六、水仙花问题
七、分解质因数问题
八、完数问题
九、求a+aa+aaa+aaaa……的值
十、小球落地弹起问题
十一、打擂台算法
十二、switch分级问题
十三、求数组中最大元素的下标,并输出存储的值
十四、阶乘计算
个人博客欢迎访问 ---- 猿客栈
一、冒泡排序
随机输入十个数,按从大到小排序
int main() -----------冒泡排序
{
int a[10];
int i,j,t;
printf("input 10 nimber:\n");
for(i=0;i<10;i++)
{
scanf("%d",&a[i]);
}
printf("\n");
for(j=0;j<9;j++)
for(i=0;i<9-j;i++)
{
if(a[i]>a[i+1])
{t=a[i];a[i]=a[i+1];a[i+1]=t;}
}
printf("sorted number:\n");
for(i=0;i<10;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
}先用for循环,循环打印十个数赋值给a[i],再通过两个嵌套for循环,第一个for循环实现循环9趟
第二个for循环实现在每一趟中比较9-j次,为什么是9-j:第一次循环完成后,第一个数成功安排在第一位,那么接下来的每一次都不用处理这第一个数,因此还剩下9-1个数需要对比,所以在进行第二趟循环时只需要比较8次,以此类推。最后对数组a[i]遍历输出
二、斐波那契函数问题
1、普通解法
求斐波那契数列的前40个数,斐波那契函数的变化规律
F1=1,F2=1,Fn=Fn-1+Fn-2(n>=3)
#include
int main()
{
int f1=1,f2=1,i;
for(i=1;i<=20;i++)
{
printf("%12d %12d",f1,f2);
if(i%2==0)printf("\n");
f1=f1+f2;
f2=f2+f1;
}
return 0;
} 主要关键代码为f1=f1+f2;f2=f2+f1;实现依次累加
在解决这个问题时出现打印结果的排列并不是预期的每四行输出一个换行符,1,1两个初始值单独换行,最后发现i是从0开始循环,所以当i=0时也就是第一次进入循环0%2==0,因此发生了换行操作。
2、用数组实现斐波那契函数
#include
int main()
{
int a[20]={1,1};
int i;
for(i=2;i<20;i++)
a[i]=a[i-1]+a[i-2];
for(i=0;i<20;i++)
{
if(i%3==0)printf("\n");
printf("%12d",a[i]);
}
return 0;
} 对数组的前两个赋初值1,1,for循环从第三个数开始,最后依次遍历数组a[i]的值
再次出现打印结果排列出现问题,原因是在if判断语句时,写在了打印a[i]语句的下方,导致了程序先打印后才进行判断
三、猴子吃桃问题
一只猴子第一天摘了n个桃,当即吃了一半又多吃了一个,第二天又吃了一半再多吃一个,直到第十天早上想吃时只剩下1个,问第一天摘了多少桃?
int main() ------猴子吃桃问题
{
int i,m=1,sum;
for(i=1;i<=9;i++)
{
m=2*(m+1);
}
printf("%d",md);
}第一天个数为n,第二天为n=n/2-1,直到第九天n/2-1=1,因此我们可以进行逆向思考,从第九天开始初值为1,变化量为2(n+1),对变化量循环九次最终得到n。
四、素数问题
求100-200之间所有的素数
#include 100-200之间的素数
int main()
{
int i,j=0,m,n;
for(n=101;n<=200;n+=2)
{
m=sqrt(n);
for(i=2;i<=m;i++)
if(n%i==0)
break;
if(i>=m)
{
printf("%d ",n);
j=j+1;
}
if(j%10==0)
printf("\n");
}
return 0;
} 判断一个数是否为素数,只需要判断这个数n能否被2~√n整除,如果不能整除那么循环不会停止直到最后一个数判断为之,循环结束后i++,而循环条件是i<√n,如果n不是素数,那么i一定大于√n。
五、最大公约数与最小公倍数
1、使用for循环实现
#include
int main()
{
int m,n,temp,i;
scanf("%d %d",&m,&n);
if(m0;i--)
{
if(m%i==0&&n%i==0)
{
printf("Max=%d\n",i); //最大公倍数
break;
}
}
printf("Min=%d\n",m*n/i); //最小公约数
return 0;
} 先判断两个输入值的大小,将两个数按从大到小的顺序互换值,将两者之间较小的数赋值给i
进入for循环,例如,6和10,将6赋值给i,进入循环,6%6=1,10%6=4,i-- == 5,进入下一次循环,直到m,n%i==0时得到最小公约数,最大公倍数:只要求出最小公约数,然后将两数之积除以最小公约数得到
2、使用辗转相除法
int main()
{
int a,b;
int t;
int num1,num2;
scanf("%d %d",&num1,&num2);
a=num1;
b=num2;
while(b!=0)
{
t=a%b;
a=b;
b=t;
}
printf("Max=%d\n",a); //最大公约数
printf("%d",num1*num2/a); //最小公倍数
return 0;
}采用辗转相除法求最小公倍数必须将输入的值赋给另一个变量,如果直接使用公式a*b/a会报错无法输出结果
在while循环中 将a%b的余数赋值给t,再将b赋值给a,t赋值给b,此时b为余数,进入下一次循环直到余数b为零,例如,输入a=6,b=8;先进行t=a%b==6%8==6,a=b=8,b=t=6进入下一次循环
t=a%b==8%6==2,a=b=6,b=t=2;进入下一次循环t=a%b==6%2==0 此时b为0结束循环。
六、水仙花问题
打印100-999中所有的水仙花数
int main()
{
int i,j,m,n,num;
for(i=100;i<1000;i++)
{
j = i/100; //百位
m = i/10%10; //十位
n = i%10; //个位
num = j*j*j+m*m*m+n*n*n;
if(num == i)
printf("%-5d",i);
}
return 0;
}其中%-5d表示的是控制五个字符格式输出,左对齐
%-md:输出格式为整形,长度为m(输出最小长度),左对齐;
七、分解质因数问题
将一个正整数分解质因数,例如将30分解成2*3*5
int main()
{
int i,m;
scanf("%d",&m);
printf("%d=",m);
for(i=2;i<=m;i++)
{
while(m!=i)
{
if(m%i == 0)
{
printf("%d*",i);
m=m/i;
}
else
break;
}
}
printf("%d",m);
return 0;
}问题思路:先用for循环,从2开始循环到这个数m为止,如果循环i等于了m说明循环已经遍历完成跳出循环,所以以这个为条件进行while循环,当i不等于这个数时,如果m%i==0说明i可以除尽m则i是m的一个因子,打印这个i,在对整数继续进行循环遍历m=m/i,直到i=m结束。
八、完数问题
找出1000以内的所有完数
一个数如果恰好等于它的因子之和,这个数就称为完数,例如6=1*2*3而6=1+2+3,所以6是完数
int main()
{
int i=0;
int arr[100]={0};
for(i=2;i<=1000;i++)
{
int m=0,sum=0;
int k=0,j=0;
for(j=1;j问题分析: 先找出每个数的因子并依次存放在数组arr[ ]中,再对数组进行遍历,依次打印并求和
如果和等于这个数则输出。
注:int m=0,sum=0;int k=0,j=0;这四个变量的赋值必须在第一个for循环中,作用是依次找出每个数的因子并判断,一个数判断结束后,进入到下一个数时再对这四个变量重新赋初值
九、求a+aa+aaa+aaaa……的值
例如a=2,n=4,求2+22+222+2222的值
int main()
{
int i=1,a,n,m;
long int count = 0,num = 0;
scanf("%d,%d",&a,&n);
while(i<=n)
{
num += a;
count += num;
a = a*10;
++i;
}
printf("%d\n",count);
return 0;
}问题分析:求解此类问题关键是求出每一项的值,而每一项的值为对(a+a*10)的循环,设每一项初值为0,总和为0,第一次进入循环第一项的值为num=num+a;num初值为0,所以第一项为a,此时num为a,总数count为a,a=a*10进入下一次循环,num=a+a*10,count=a+(a+a*10),再进入下一次循环直到n为止。
十、小球落地弹起问题
一小球从100米高度自由落下,每次落地后反弹回原高度的一半再落下,求它在第十次落地时共经过多少米?第十次反弹多高?
int main()
{
int i;
float h=100.0,s=h/2;
for(i=1;i<=10;i++)
{
h = h + 2*s;
s = s/2;
}
printf("h=%f,s=%f\n",h,s);
return 0;
}十一、打擂台算法
有一个3*4的矩阵,要求编程求出矩阵中最大的元素,以及最大元素的位置
int main()
{
int a[3][4]={{12,14,17,18},{4,67,3,2},{4,58,1,7}};
int row,colum,i,j,max;
max=a[0][0];
for(i=0;i<3;i++)
for(j=0;j<4;j++)
{
if(a[i][j]>max)
{
max=a[i][j];
row=i;
colum=j;
}
}
printf("%d\n%d\n%d\n",max,i,j);
return 0;
}问题分析:首先定义最大值为数组初值[0][0],再用冒泡排序,在三行四列中进行循环,使用if判断如果a[i][j]>max,则将a[i][j]的值赋给max,将i,j值分别存储。
十二、switch分级问题
给出一个百分制成绩,要求输出成绩等级'A','B','C','D','E'。90分以上为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
int main()
{
int sc,i;
printf("please input you score:");
scanf("%d",&sc);
i=sc/10;
printf("your score is:");
switch(i)
{
case 1:
case 2:
case 3:
case 4:
case 5:printf("E");break;
case 6:printf("D");break;
case 7:printf("C");break;
case 8:printf("B");break;
case 9:
case 10:printf("A");break;
}
return 0;
}注意:switch语句括号中的数据必须是整数类型包括字符型。
十三、求数组中最大元素的下标,并输出存储的值
int fun(int *s,int t,int *k)
{
int i;
*k = 0;
/* *k所指的数为下标值 */
for(i=0;i十四、阶乘计算
float fun(int m,int n)
{
float p1,p2,p3,p4;
/*m的阶乘*/
for(i=1;i<=m;i++)
p1 *= i;
/*n的阶乘*/
for(i=1;i<=n;i++)
p2 *= i;
/*m-n的阶乘*/
for(i=1;i<=m-n;i++)
p3 *= i;
p4 = p1/(p2*p3);
return p4;
}