leetcode309最佳买卖股票时机含冷冻期

给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格。设计一个算法计算出最大利润。

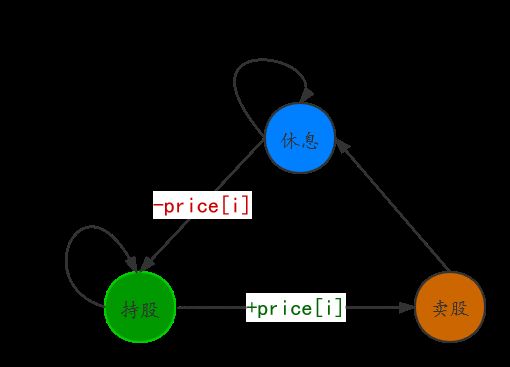
搞清楚有哪些状态，以及状态怎么转移。画个图，看第$i$天的三种状态的可能转移情况。注意：此题需要考虑冷却期。

题目

给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格 。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票：

• 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
• 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

示例:

输入: [1,2,3,0,2]
输出: 3 
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

思路

状态

对于某一天$i$，有三种状态$j$：

• 0 休息，即手上没有股票且当天也没有卖股。
• 1 持股
• 2 卖股

相应的，使用$dp[i][j]$表示第$i$天，状态为$j$时，手里所有的最大现金数。

先列出昨天到今天状态的所有转移情况：

（1）昨天为休息的状态：

昨天状态	今天状态	是否可以进行状态转移
0	0	可以，继续休息
0	1	可以，昨天没有股票，今天可以买股
0	2	不可以，卖股之前必须先手里有股票

（2）昨天为持股的状态：

昨天状态	今天状态	是否可以进行状态转移
1	0	不可以，持股想要休息之前，必须先将股票卖掉
1	1	可以，继续持有股票
1	2	可以，今天可以将股票卖出

（3）昨天为卖股的状态：

昨天状态	今天状态	是否可以进行状态转移
2	0	可以，昨天卖股，今天可以休息
2	1	不可以，必须进入冷却期，即卖出股票的第二天不能买股
2	2	不可以，卖股之前必须持有股票

用图形直观的表示状态的情况，如下图所示：

状态转移

$dp[i][0]=max(dp[i-1][0],dp[i-1][2])$

$dp[i][1]=max(dp[i-1][0]-price[i],dp[i-1][1])$

$dp[i][2]=dp[i-1][1]+price[i]$

初始化

$dp[0][0]=0$：来的第一天休息，手里没钱

$dp[0][1]=-price[0]$来的第一天就买股了，手里欠钱

$dp[0][2]=0$：来的第一天就卖股了（当然是不可能的），手里这是也是现金0

代码

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0 ){
            return 0;
        }
        int[][] dp = new int[prices.length + 1][3];
        dp[0][0] = 0;//休息
        dp[0][1] = -prices[0];//持股
        dp[0][2] = 0;//卖股
        for(int i = 1;i < prices.length; i++){
            dp[i][0] = Math.max(dp[i - 1][0],dp[i - 1][2]);
            dp[i][1] = Math.max(dp[i -1][0] - prices[i],dp[i - 1][1]);
            dp[i][2] = dp[i - 1][1] + prices[i];
        }
        return Math.max(dp[prices.length - 1][0],dp[prices.length - 1][2]);
    }
}

时间复杂度——$O(N)$

空间复杂度——$O(N)$

空间优化

这里我们只需要昨天的三种状态的现金拥有情况。

代码一

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0 ){
            return 0;
        }
        int[][] dp = new int[2][3];
        dp[0][0] = 0;//休息
        dp[0][1] = -prices[0];//持股
        dp[0][2] = 0;//卖股
        for(int i = 1;i < prices.length; i++){
            dp[i%2][0] = Math.max(dp[(i - 1)%2][0],dp[(i - 1)%2][2]);
            dp[i%2][1] = Math.max(dp[(i - 1)%2][0] - prices[i],dp[(i - 1)%2][1]);
            dp[i%2][2] = dp[(i - 1)%2][1] + prices[i];
        }
        return Math.max(dp[(prices.length-1)%2][0],dp[(prices.length - 1)%2][2]);
    }
}

时间复杂度——$O(N)$

空间复杂度——$O(1)$

代码二

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0 ){
            return 0;
        }
        int[] dp = new int[3];
        dp[0] = 0;//休息
        dp[1] = -prices[0];//持股
        dp[2] = 0;//卖股
        int pre0 = dp[0];
        int pre1 = dp[1];
        for(int i = 1;i < prices.length; i++){
            dp[0] = Math.max(dp[0],dp[2]);
            dp[1] = Math.max(pre0 - prices[i],dp[1]);
            dp[2] = pre1 + prices[i];
            pre0 = dp[0];
            pre1 = dp[1];
        }
        return Math.max(dp[0],dp[2]);
    }
}

由于$dp[1],dp[2]$分别需要上一天的$dp[0],dp[1]$，为了防止可能会覆盖的情况的，需要再定义两个变量记录上一次的情况。

时间复杂度——$O(N)$

空间复杂度——$O(1)$

参考

1、买卖股票的一系列问题