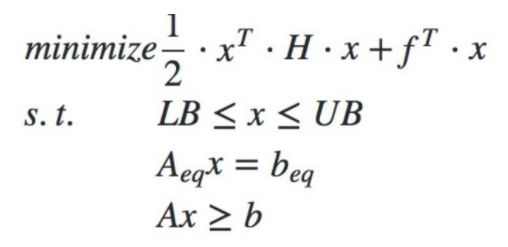路径规划的二次规划方法-知识总结

路径规划的二次规划方法-知识总结

关于路径规划的优化方法，常见的有二次规划QP，样条二次规划SQP，这里以Apollo的优化方法为例子，作为一个笔记的记录，记录一些个人的问题。

二次规划基础知识

二次规划基础：二次型、正定矩阵、海塞矩阵

【机器学习】二次规划

常用二次规划求解器

OSQP :使用ADMM方法求解。 对于规模大的，含有大量等式或不等式约束的问题有较好的求解效率。
qpOASES: 用可行域法，对于约束较少的小规模问题，qpOASES求解更快。

Apollo参考线平滑方法

采用QP形式进行优化：

这些文章讲得还不错：
自动驾驶之轨迹规划5——Apollo规划中的离散点曲线平滑数学原理

Apollo参考线优化之DiscretePointsReferenceLineSmoother

无人驾驶算法——Baidu Apollo代码解析之ReferenceLine Smoother参考线平滑

要注意的是，二次规划QP的形式如何去构建，为什么要那样构建：
（1）P矩阵：
这里的P矩阵搭建还是这一篇的描述会比较好：
Apollo参考线优化之DiscretePointsReferenceLineSmoother
例子举例不错，但是这里有些问题：
a. 首先，这里没有将权重变量添加进去：

这里的X，Y，Z应该还得乘以每个cost对应的权重变量。另外这里的x,y,z表示的是一个坐标值，而不是一个值，所以I才是2X2单位矩阵。

b. 第二，这里的P为什么只取上三角呢？
值得注意的是，这篇博客它没有取上三角：

无人驾驶算法——Baidu Apollo代码解析之ReferenceLine Smoother参考线平滑

但是从源码和其他博客来说，确实取了上三角：

原因呢？个人见解为：
二次规划问题的P矩阵是一个半正定矩阵，上三角的特征值为对角线元素，只要保证对角线元素大于0，就可以保证特征值都大于0，也即确保P矩阵是正定矩阵，存在全局最优解。

q矩阵的搭建比较简单，注意也要将权重代入：

补充：

正定矩阵是一种实对称矩阵，正定矩阵在实数域上是对称矩阵，这里的数值都是实数，这篇文章：
为什么非零实对称矩阵一定是正定矩阵 证明了实对称矩阵一定是正定矩阵。

二次规划的类别

所谓二次规划问题，就是目标函数为二次函数，约束函数为线性函数的最优化问题。
我目前接触的有三种：二次规划（QP），序列二次规划（SQP），二次规划样条路径优化。二次规划可看前文的参考线平滑例子。
关于序列二次规划，约束为非线性约束，可看介绍：
序列二次规划——SQP

二次规划样条路径优化目标：

例子可看：
技术文档 | 二次规划（QP）样条路径

二次规划（QP）样条路径优化

【规划】Apollo QSQP接口详解

【路径规划】OSQP曲线平滑 公式及代码

apollo qp_speed_optimzer

二次规划（QP）和序列二次规划（SQP）：
二次规划（QP）求解与序列二次规划（SQP）求解非线性规划问题

二次规划的求解

当然，上面都是浅浅地了解学习。还得稍微了解一下求解过程。常用的求解器已经列出来：
OSQP :使用ADMM方法求解。 对于规模大的，含有大量等式或不等式约束的问题有较好的求解效率。
qpOASES: 用可行域法，对于约束较少的小规模问题，qpOASES求解更快。

那么有必要简单理解求解过程：
二次规划问题(qp)和序列二次规划问题(sqp)的简单理解
耗时对比：
关于Quadratic Programming(QP)算法和NMPC求解器(SQP)的研究

对自动驾驶中路径规划算法的思考

(附代码)QP求解器对比

Apollo EM Planner和Lattice Planner的对比

（1） 优缺点
从公式来看，Lattice是在已知轨迹的情况下评估，考虑的因素更为具体和全面。而EM是在轨迹未知的情况下求轨迹，考虑的因素更单纯，公式形式更简单。

总体来说，二者的代价函数均是用来解决同一问题的，因此考虑的因素大体一致，轨迹的平滑、避免碰撞、与参考方程（参考线、前步输出、目标速度等guidance）吻合等因素均纳入了考虑。但是，二者的代价函数没有必然联系。

（2）耗时对比
a. 先看EM Planner，求解器是qpOASES。路径和速度的DP过程其实不怎么耗时，大概只需要2ms，耗时主要在QP的构建和求解过程，以及轨迹数据的坐标系转换（从笛卡尔坐标系转为Frenet），代码测试耗时如下（根据移植Apollo3.5版本的EM）：

过程	耗时（ms），有一定误差偏差范围
路径规划DP	1.9
路径规划QP	56
笛卡尔坐标系转为Frenet	50
Frenet 转为笛卡尔坐标系	0.08
速度规划DP	0.7
速度规划QP	2.3
程序总耗时	111

这里的路径规划QP 和速度规划QP 为什么会差别这么大呢？因为QP过程包含了求解P，q矩阵，添加约束，调用qpOASES求解器求解等，经过测试每个步骤的耗时，发现，路径规划QP的AddKernel()函数，耗时很多，约52ms，求解过程也只有0.3ms左右，而速度规划QP过程的AddKernel()函数耗时约0.5ms，求解过程耗时约1.7ms。那么问题来了，为什么，路径规划QP的AddKernel()函数的耗时这么多呢？原来是在添加引导线约束那里，多了笛卡尔坐标系转为Frenet 的步骤。。。速度规划的QP不需要进行坐标转换。

这里要说的是，源先的代码写得有的奇怪：我们在路径DP过程的时候，已经是在SL下进行采样，然后为了可以显示DP路径数据，将Frenet 转为笛卡尔坐标系，这里耗时0.08ms，很少，然后获取历史轨迹（引导线），历史轨迹其实已经包含了XY和SL坐标系，添加引导线约束源码是这样：

void QpSplinePathGenerator::AddHistoryPathKernel() {
  if (last_discretized_path_ == nullptr) {
    return;
  }

  PathData last_path_data;
  last_path_data.SetReferenceLine(&reference_line_);
  last_path_data.SetDiscretizedPath(*last_discretized_path_);

  std::vector<double> history_s;
  std::vector<double> histroy_l;

  for (size_t i = 0; i < last_path_data.frenet_frame_path().size(); ++i) {
    const auto p = last_path_data.frenet_frame_path().at(i);
    history_s.push_back(p.s());
    histroy_l.push_back(p.l() - ref_l_);
  }

  Spline1dKernel* spline_kernel = spline_solver_->mutable_spline_kernel();
  spline_kernel->AddReferenceLineKernelMatrix(
      history_s, histroy_l, qp_spline_path_config_.history_path_weight());
}

其中，SetDiscretizedPath这个函数耗时约52ms。但是其实我们应该可以换一种写法，可以在构造函数里面就获取历史轨迹的frenet坐标系内容，并赋值给last_frennet_path_：

void QpSplinePathGenerator::AddHistoryPathKernel()
{
  if (last_discretized_path_ == nullptr || last_frennet_path_ == nullptr)
  {
    return;
  }
  //last_path_data.SetReferenceLine(&reference_line_);
  //last_path_data.SetDiscretizedPath(*last_discretized_path_);
  
  std::vector<double> history_s;
  std::vector<double> histroy_l;

  for (size_t i = 0; i < last_frennet_path_->size(); ++i)
  {
    const auto p = last_frennet_path_->at(i);
    history_s.push_back(p.s);
    histroy_l.push_back(p.d - ref_l_);
  }

  Spline1dKernel *spline_kernel = spline_solver_->mutable_spline_kernel();
  spline_kernel->AddReferenceLineKernelMatrix(history_s, histroy_l, Config_.history_path_weight);
}

这样耗时就减半啦，整个过程耗时变成约60ms，而且没有轨迹生成也没有异常。但是，在QpSplinePathGenerator::Generate函数里有一语句： path_data->SetDiscretizedPath(DiscretizedPath(path_points));
它是对优化后的路径进行转化的，就删除不掉，因为还是得有笛卡尔坐标系，合成的时候才能直接转换。所以，最后EM Planner的总耗时为：57.6933ms - 63.3948ms。

b. Lattice Planner可分为采样规划和二次规划，明显采样规划耗时更多。
采样规划的耗时表如下：

主要过程	耗时（ms），有一定误差偏差范围
轨迹生成	0.512495 - 1.09752
轨迹筛选（评价+碰撞检测）	53.8503 - 93.9556
程序总耗时	54 - 95

遇到障碍物的时候，评价函数耗时可谓是剧增，这是采样方法的缺点。

二次规划的耗时表如下：

主要过程	耗时（ms），有一定误差偏差范围
轨迹生成	1.97102- 2.04251
轨迹筛选（评价+碰撞检测）	2.12562 - 11.4235
程序总耗时	4 - 14

总结

总的来说，路径的优化方法还是比路径的采样方法好，耗时少，但是采样也有采样的优点。每个场景结合不同的规划算法，会比较合适。