Unity—3D数学-Vector3
补发昨天的,今明两天还是继续3D数学,学习剧透一下:25、26号会发布一篇不同版本的“合成大西瓜”的详细讲解,期待一下呦!结尾有彩蛋呦!
每日一句:少年心怀乌托邦,心仍向阳肆生长
目录
Vector3
向量
向量的大小
向量的方向
向量运算
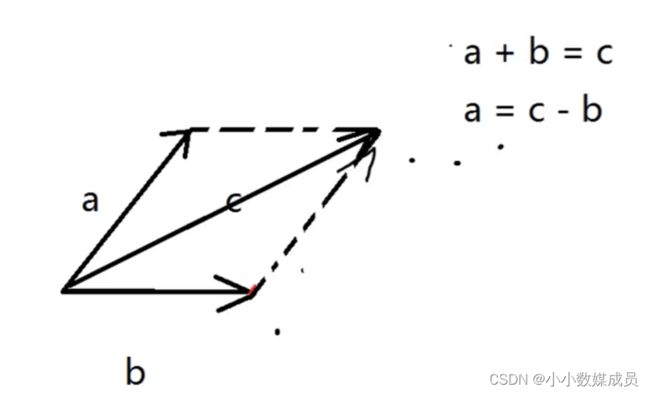
向量相减、相加
需求:t3沿着t1-t2的方向移动
向量与标量的乘除
角度度量方式:
角度Degree与弧度Radin
角度与弧度的换算
三角函数
反三角函数
练习:计算物体右前方30度,10米远坐标
Vector3
向量
向量的大小
API:float dis=Vector.magnitude
Vector3 pos=this.transform.position;
//表示向量的大小三种形式
float m01=Mathf.Sqrt(Mathf.Pow(pos.x,2)+Mathf.Pow(pos.y,2)+Mathf.Pow(pos.z,2));
//公式
float m02=pos.magnitude;//API
float m03=Vector3.Distance(Vector3.zero,pos);//距离
向量的方向
获取向量方向也称“标准化向量”,“归一化向量”或“单位向量”,即将向量拉长或缩短,使模长等于1
API:Vector3 n02=vector.normalized;
n02为vector的单位向量
private void Update()
{
Vector3 pos = this.transform.position;
Vector3 n01 = pos / pos.magnitude;
Vector3 n02 = pos.normalized;
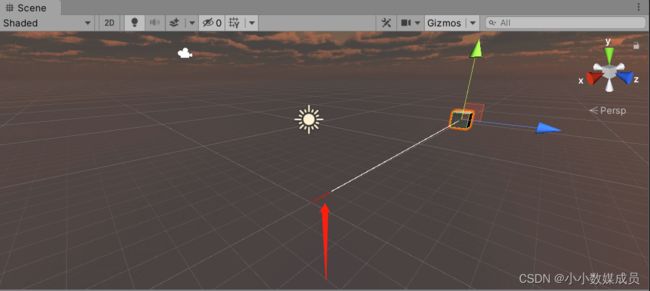
Debug.DrawLine(Vector3.zero, pos);
Debug.DrawLine(Vector3.zero, n02, Color.red);
}
向量运算
向量相减、相加
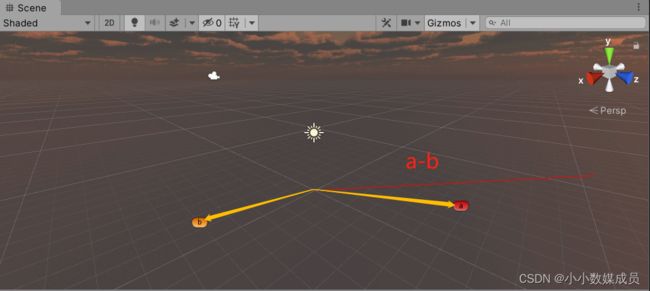
Vector3 relativeDirection=t1.position-t2.position;
大小:两点间距离
方向:指向被减向量
因为t1,t2是世界坐标,所以t1-t2实际位置平移到世界坐标原点
需求:t3沿着t1-t2的方向移动
public Transform t1, t2, t3;
private void Update()
{
Vector3 relativeDirection = t1.position - t2.position;
if (Input.GetKeyDown(KeyCode.A))
{
t3.Translate(relativeDirection.normalized);
}
Debug.DrawLine(Vector3.zero, relativeDirection, Color.red);
}t3.Translate(relativeDirection.normalized);//获取方向,避免两个物体间距对速度造成影响
=t3.position = t3.position + relativeDirection.normalized;
向量与标量的乘除
乘法:该向量的各分量与标量相乘k[x,y,z]=[kx,ky,kz]
几何意义:缩放向量长度
需求:有一个长度为8的向量,怎么得到长度为13的向量
先把向量normalized,再乘13
角度度量方式:
角度Degree与弧度Radin
两条射线从圆心向四周射出,形成一个夹角和夹角正对的一段弧度。
1弧度:弧长等于圆的半径时,夹角为1弧度
半圈=π(3.14159)弧度
角度与弧度的换算
1弧度=180度/π 1角度=π/180度
API 弧度=角度数*Mathf.Deg2Rad;
API 角度=弧度数*MAthf.Rad2Deg;
角度—>弧度
float d1=60;
float r1=d1*Mathf.PI/180;
float r2=d1*Mathf.Deg2Rad;
弧度—>角度
float r1=3;
float d1=r1*180/Mathf.PI;
float d2=r1*Marhf.Rad2Deg;
三角函数
建立了直角三角形中角与边长比值的关系
可用于根据一边一角,计算另一边长
公式:sin x=a/c cos x=b/c tan x=a.b
API:
Mathf.Sin(float radian弧度);
Mathf.Cos(float radian弧度);
Mathf.Tan(float radian弧度);
30度—>弧度:30*Mathf.Deg2Rad//弧度到度换算常量
·已知角度x和邻边a,求对边
float x = 50, b = 20;
float a = Mathf.Tan(Mathf.Deg2Rad * x) * b;
反三角函数
可用于根据两边长计算角度
公式:反正弦 arcsin a/c=x arccos b/c=x arctan a/b=x
API:
Mathf.Asin(float radin);
Mathf.Acos(float radin);
Mathf.Atan(float radin);
·已知边长a和b,求角度angle
float a = 30, b = 20;
float angle = Mathf.Atan(a / b) * Mathf.Rad2Deg;
练习:计算物体右前方30度,10米远坐标
Vector3 worldPoint=this.transform.TransformPoint(Vector3 point)//将点从自身坐标系转换成世界坐标系
public static void DrawLine (Vector3 start, Vector3 end, Color color= Color.white, float duration= 0.0f, bool depthTest= true);//在指定的起始点与结束点之间绘制一条直线。
private void Update()
{
float x = Mathf.Sin(30 * Mathf.Deg2Rad) * 10;
float z = Mathf.Cos(30 * Mathf.Deg2Rad) * 10;
Vector3 worldPoint = transform.TransformPoint(x, 0, z);
Debug.DrawLine(this.transform.position, worldPoint, Color.blue);
}彩蛋!!!
面向对象的三大特点:封装性、继承性、多态性
1.封装性:隐藏对象的属性和实现细节,仅对外公开接口,控制在程序中属性的读和修改的访问级别,将抽象得到的数据和行为(或功能)相结合,形成一个有机的整体(“类”)。(将数据和行为相结合,通过行为约束代码修改数据;将一些复杂的逻辑进行包装,别人只需传入所要的参数,就可以得到想要的结果)
2.继承性:就是子类继承父类的特征和行为,使得子类对象(实例)具有父类的实例域和方法,或子类从父类继承方法,使得子类具有父类相同的行为。
3.多态性:多态同一个行为具有多个不同表现形式或形态的能力。是指一个类实例(对象)的相同方法在不同情形有不同表现形式。多态机制使具有不同内部结构的对象可以共享相同的外部接口。意味着,虽然针对不同对象的具体操作不同,但通过一个公共的类,它们(那些操作)可以通过相同的方式予以调用。
多态存在的三个必要条件:
- 继承
- 重写(子类继承父类后对父类方法进行重新定义)
- 父类引用指向子类对象
多态其实是在继承的基础上的。
封装 可以增强数据的增强型,隐藏实现细节,使得代码模块化;继承可以对原有类的功能进行扩展,提高了代码的重复性和开发效率,增强软件可维护性的重要手段,符合开闭原则;而多态则是为了实现另一个目的——接口重用!
*开闭原则的含义是:当应用的需求改变时,在不修改软件实体的源代码或者二进制代码的前提下,可以扩展模块的功能,使其满足新的需求。